
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика вращательного движения твердого телаСодержание книги
Поиск на нашем сайте
Закон динамики вращательного движения твердого тела в проекции на ось вращения z:
где
7-2. Тонкий однородный стержень массы m и длины l может вращаться в вертикальной плоскости без трения вокруг горизонтальной оси, проходящей через его конец. Стержень располагают под углом a к горизонту и отпускают без толчка. Найдите его угловое ускорение в начальный момент времени. m = 1 кг, l = 1 м, a = 30°, g = 10 м/с2.
m = 1 кг, l = 1 м, F = 3 Н, Мтр = 1 Н×м.
7-7. Некоторое тело вращается вокруг закрепленной оси без трения. Его момент импульса относительно оси вращения зависит от времени по закону 7-8. Тело вращается вокруг закрепленной оси с угловым ускорением, зависимость от времени которого задается графиком. Момент инерции тела относительно оси вращения равен I. Найти момент импульса тела в момент времени
а) отношение модулей моментов сил; б) на сколько отличаются модули моментов сил, действующих на тело в моменты времени 7-10. Некоторое тело вращается вокруг закрепленной оси без трения. Его момент импульса относительно оси вращения зависит от времени по закону
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

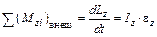 , где I z– момент инерции тела относительно оси вращения,
, где I z– момент инерции тела относительно оси вращения, 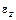 – проекция углового ускорения на ось вращения,
– проекция углового ускорения на ось вращения, 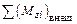 – сумма проекций внешних моментов сил,
– сумма проекций внешних моментов сил,  – проекция момента импульса твердого тела.
– проекция момента импульса твердого тела.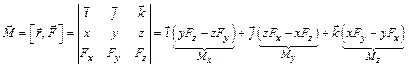 ,
, – радиус вектор точки приложения силы
– радиус вектор точки приложения силы 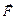 .
. 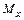 ,
, 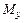 ,
, 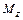 – проекции момента силы. Модуль момента силы
– проекции момента силы. Модуль момента силы 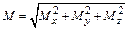 или
или 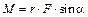 , где a – угол между силой
, где a – угол между силой 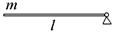 7-1. Тонкий однородный стержень массы m = 1 кг и длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. В оси действует момент сил трения Мтр. = 1 Н×м. Стержень приводят в горизонтальное положение и отпускают без толчка. Найдите угловое ускорение в начальный момент времени. g = 10 м/с2.
7-1. Тонкий однородный стержень массы m = 1 кг и длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. В оси действует момент сил трения Мтр. = 1 Н×м. Стержень приводят в горизонтальное положение и отпускают без толчка. Найдите угловое ускорение в начальный момент времени. g = 10 м/с2.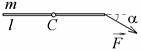 7-3. Тонкий однородный стержень массы m = 1 кги длины l = 1 м может вращаться в горизонтальной плоскости без трения вокруг вертикальной оси С, проходящей через середину стержня. К концу стержня в плоскости вращения под углом a = 30° к стержню прикладывают силу
7-3. Тонкий однородный стержень массы m = 1 кги длины l = 1 м может вращаться в горизонтальной плоскости без трения вокруг вертикальной оси С, проходящей через середину стержня. К концу стержня в плоскости вращения под углом a = 30° к стержню прикладывают силу 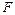 =1 Н. Найдите угловое ускорение стержня в начальный момент времени.
=1 Н. Найдите угловое ускорение стержня в начальный момент времени.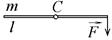 7-4. Тонкий однородный стержень массы m и длины l может вращаться в горизонтальной плоскости вокруг вертикальной оси С, проходящей через середину стержня. В оси действует момент силы трения Мтр. К концу стержня в плоскости вращения перпендикулярно стержню прикладывают силу
7-4. Тонкий однородный стержень массы m и длины l может вращаться в горизонтальной плоскости вокруг вертикальной оси С, проходящей через середину стержня. В оси действует момент силы трения Мтр. К концу стержня в плоскости вращения перпендикулярно стержню прикладывают силу 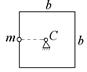 7-5. Тонкая однородная пластина в виде квадрата со стороной b может вращаться без трения в вертикальной плоскости вокруг горизонтальной оси, проходящей через центр масс С. Момент инерции пластины относительно оси С равен I. К середине стороны квадрата приклеили маленький грузик массы m и отпустили без толчка. В начальный момент сторона квадрата была вертикальна. Найдите угловое ускорение получившейся фигуры в начальный момент времени. m = 1 кг, I = 1
7-5. Тонкая однородная пластина в виде квадрата со стороной b может вращаться без трения в вертикальной плоскости вокруг горизонтальной оси, проходящей через центр масс С. Момент инерции пластины относительно оси С равен I. К середине стороны квадрата приклеили маленький грузик массы m и отпустили без толчка. В начальный момент сторона квадрата была вертикальна. Найдите угловое ускорение получившейся фигуры в начальный момент времени. m = 1 кг, I = 1 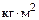 , b = 1 м, g = 10 м/с2.
, b = 1 м, g = 10 м/с2.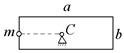 7-6. Тонкая однородная прямоугольная пластина со сторонами b и a может вращаться без трения в вертикальной плоскости вокруг горизонтальной оси, проходящей через центр масс С. Момент инерции пластины относительно оси С равен I. К середине стороны пластины приклеили маленький грузик массы m и отпустили без толчка. В начальный момент сторона пластины была вертикальна. Найдите угловое ускорение получившейся фигуры в начальный момент времени.
7-6. Тонкая однородная прямоугольная пластина со сторонами b и a может вращаться без трения в вертикальной плоскости вокруг горизонтальной оси, проходящей через центр масс С. Момент инерции пластины относительно оси С равен I. К середине стороны пластины приклеили маленький грузик массы m и отпустили без толчка. В начальный момент сторона пластины была вертикальна. Найдите угловое ускорение получившейся фигуры в начальный момент времени.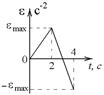 m = 1 кг, I = 1
m = 1 кг, I = 1 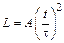 . Через время t =1 с тело имеет угловое ускорение e. Найти момент инерции тела, если t =1 с. A = 1
. Через время t =1 с тело имеет угловое ускорение e. Найти момент инерции тела, если t =1 с. A = 1 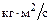 , e = 1 рад/с2.
, e = 1 рад/с2.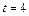 с, если
с, если 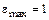 с–2. I = 1
с–2. I = 1 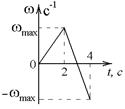 7-9. Тело вращается вокруг закрепленной оси с угловой скоростью, зависимость от времени которой задается графиком. Момент инерции тела относительно оси вращения равен I. Найти
7-9. Тело вращается вокруг закрепленной оси с угловой скоростью, зависимость от времени которой задается графиком. Момент инерции тела относительно оси вращения равен I. Найти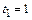 с и
с и 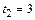 с.
с. 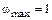 с–1, I = 1
с–1, I = 1 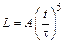 . Через время t =1 с тело имеет угловое ускорение e. Найти момент инерции тела, если t =1 с. A = 1
. Через время t =1 с тело имеет угловое ускорение e. Найти момент инерции тела, если t =1 с. A = 1 


