
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логическое обоснование методов расчетаСодержание книги
Поиск на нашем сайте
(Данное приложение не является частью документа ASME PTC 10-1997.)
E.1 ЦЕЛЬ Целью данного приложения является описание модели задачи, базовой теории, а также упрощающих допущений, которые были применены в настоящей Методике. E.2 МОДЕЛЬ ЗАДАЧИ Конечной целью проведения испытаний на основании настоящей Методики является определение рабочих характеристик компрессора для заданного набора условий. То есть определить взаимосвязь с формой
Зависимый параметр = F (множество независимых параметров)
Примером зависимого параметра могут выступать давление на выходе, напор, КПД и т.д. Среди независимых параметров выделяют геометрию агрегата, частоту вращения, расход, параметры газа на входе, свойства газа и т.д. Функциональная зависимость f неизвестна. Данная величина должна быть определена в ходе проведения испытаний. Множество независимых параметров представляют собой заданные эксплуатационные условия. На практике, обстановка во время испытаний такова, что один или более из этих параметров исключается из перечня тех величин, которые оказывают влияние на требуемые значения для заданных эксплуатационных условий. В таких случаях должны быть предприняты меры в целях определения влияния отклонений. Одним из методов является применение размерного анализа.
E.2.1 Размерный анализ. Теория размерного анализа и подобия рассматривается в документе PTC 19.23, Инструкция по проведению испытаний методом моделирования, а также множестве учебников по динамике жидкостей и газов. В сущности там представлена информация о том, как в поставленной задаче снизить количество параметров, которые выражены в размерном виде. Этого можно достичь за счет группировки параметров, имеющих размерность в безразмерные комплексы.
E.2.2 Базовая модель. Рассмотрение простой математической модели рабочих характеристик компрессора демонстрирует основные возможности размерного анализа в том виде, в котором они применяются в настоящей Методике. Простой общепринятый набор зачастую применяемых безразмерных параметров задан следующими выражениями:
ηp = F1 (ɸ, Mm, Rem, характеристики газа, выраженные в форме безразмерном виде ) μ p = F2 (ɸ, Mm, Rem, характеристики газа, выраженные в форме безразмерном виде ) μ in = F2/ F1
Безразмерные параметры заданы как функция от переменных, имеющих размерность
с учетом,
Параметры газа … в соответствии с типами газа
При осуществлении размерного анализа предполагается, что все переменные, которые влияют на термодинамические и гидродинамические характеристики компрессора, включены в расчет. В таком случае, различные наборы размерных переменных, которые комбинируются в целях формирования идентичных наборов независимых безразмерных комплексов (ɸ, Mm, Rem, характеристики газа), будут иметь связанные с ними идентичные значения параметров η, μ p и μ in. Базовая модель в основном используется для того, чтобы надлежащим образом описать основные особенности рабочих характеристик компрессора. В базовой модели заключено прямое преимущество, заключающееся в уменьшении количества параметров, которые должны быть приняты к учету при разработке программы испытаний. Однако, не менее важно то, что базовая модель обеспечивает наличие средств учета неизбежных отклонений от целевых параметров заданных эксплуатационных условий. Например, с помощью базовой модели можно установить соответствующую величину оборотов при проведении испытаний для того, чтобы скомпенсировать влияние входной температуры при проведении испытаний, которая отличается от температуры для заданных эксплуатационных условий.
E.2.3 Допустимые отклонения. Зачастую выполнение всех требований в части независимых безразмерных параметров является нецелесообразным. Данная ситуация может быть урегулирована путем принятия допустимых отклонений для некоторых независимых безразмерных комплексов. Допущение заключается в том, что предельные значения, установленные для указанных отклонений, преобразуют воздействие на зависимые параметры к пренебрежимо малым или прогнозируемым значениям. Нижеуказанный подход применяется в настоящей Методике.
E.2.3.1 Число Маха. Предполагается, что отклонения в величине числа Маха будут иметь все большую важность с ростом значения самого числа Маха агрегата. Данная взаимосвязь отражена в значениях допустимых отклонений, которые приведены в Табл. 3.2 или Рис. 3.2 и 3.3. Допущение гласит о том, что влияние будет считаться пренебрежимо малым в тех случаях, когда отклонение будет укладываться в границы диапазона, заданного предельными значениями.
E.2.3.2 Характеристики газа. Допустимые отклонения от уравнений идеального газа как для испытательных газов, так и для заданных газов, приведены в Табл. 3.3. В тех случаях, когда предельные значения превышены, газ должен рассматриваться в качестве реального.
E.2.3.3 Число Рейнольдса. Допустимые отклонения в части значений числа Рейнольдса агрегата приведены в Табл. 3.2 и на Рис. 3.4. E.2.3.4 Отношение удельных объемов. Упоминаемые выше допустимые отклонения независимых безразмерных комплексов могут быть объединены в целях изменения величины отношения удельных объемов между входным и выходным устройством компрессора. Как результат, на параметр rv (отношение объемов) накладываются дополнительные ограничения, как показано в Табл. 3.2. Результаты влияния отклонения величины отношения объемов считаются пренебрежимо малыми, в тех случаях, когда предельные значения не превышены.
E.2.4 Вторичные потоки. Базовая модель рабочих характеристик компрессора предполагает наличие одного потока на входе и на выходе. В реальных условиях в узел компрессора могут входить или выходить вторичные потоки. Примером являются параллельные потоки и течи. Указанные вторичные потоки приводят к образованию дополнительных безразмерных комплексов. Каждый дополнительный входящий поток соотносится с параметрами расхода и характеристиками газа, или тремя дополнительными независимыми переменными. Если мы используем объемный расход, энтальпию и плотность в целях определения параметров потоков, мы сможем сформировать три дополнительных независимых безразмерных комплекса посредством привязки характеристик основного потока,
где х обозначает принадлежность величины к параллельному потоку, а m указывает на ссылочную величину для основного потока. Подход, используемый в настоящей Методике, заключается в выполнении требования, согласно которому отношение расходов через параллельный поток к основному оставалось в пределах, указанных в Табл. 3.5 (прим. перев: Табл. 3.5 отсутствует в тексте оригинала, ошибочная ссылка) или соответствовало характеристикам течей согласно данным пункта 3.3.6. В тех случаях, когда данные ограничения соблюдаются, делается предположение о том, что влияние зависимые безразмерные комплексы является пренебрежимо малым. Специальных ограничение на отношения параметров плотности или энтальпии не накладывается. Предполагается, что отклонения в значениях данных параметров будут оказывать пренебрежимо малое влияние на зависимые безразмерные комплексы. В тех случаях, когда полное (совершенное) смешение потоков на входе до сжатия имеет малую вероятность, данное предположение не может рассматриваться в качестве истинного. В таких случаях, стороны, участвующие в проведениях испытаний, по взаимному соглашению могут принять решение об ограничении указанных отношений параметров. Отклонения в таких вторичных безразмерных комплексах влияют на результат с точки зрения размерности. Данная особенность учтена в процедура расчета. E.2.5 Сводная информация о модели. Информация о Модели рабочих характеристик из настоящей Методики может быть кратко сформулирована как указано ниже:

Для заданного значения коэффициента расхода ɸ, допустимы некоторые отклонения в оставшихся независимых безразмерных комплексах. Ограничение в величине отношения объемов служит для того, чтобы лимитировать влияние совокупных отклонений в других безразмерных комплексах. Первые три зависимых группы имеют тот же формат, как и те, которые были приведены в предыдущих изданиях настоящей Методики. Четвертая, Ω sp, является новой в данном издании и выступает здесь в качестве явного параметра. Это коэффициент мощности, который принимает разные формы для метода теплового баланса и метода прямого замера мощности на валу. Он связан с другими зависимыми параметрами, однако непосредственно используется в целях учета в части сложных структур данных.
E.3 БЕЗРАЗМЕРНЫЕ ПАРАМЕТРЫ. Единицы измерения и размерные константы должны соответствовать системе размерностей, выбранной для выполнения расчетов.
E.3.1 Входные и выходные условия. Структура модели задачи такова, что необходимостью является точное определение входных и выходных условий, используемых при вычислении безразмерных комплексов. Условия на выходе – это условия полного торможения потока в точке замера выходных параметров. Входные условия – это параметры полного торможения, соотнесенные с потоком, который попадает на рабочее колесо; входные условия обозначаются подстрочным индексом i в выражениях термодинамических характеристик. Для простого отдельного входящего потока, входные условия – это параметры полного торможения на входном фланце. В случае наличия нескольких входящих потоков, входные условия – это параметры полного торможения, вычисленные из условий смешения потоков, характеристики которых были определены отдельно для каждого из них. Стандартная схема выполнения расчета приведена в подпункте Е.5.
E.3.2 Коэффициент расхода. Коэффициент расхода вычисляется в соответствии с формулой
где w rotor = массовый расход на входе в роторную часть (массовый расход сжатой среды) pi = полная плотность на входе N = частота вращения ротора D диаметр по концевой кромке лопатки первого рабочего для центробежных компрессоров. D диаметр в точке максимального сечения входной кромки лопаток ротора первой ступени для осевых компрессоров. Массовый расход на входе в роторную часть вычисляется с должным учетом всех входящих и выходящих потоков и течей всех каскадов.
E.3.3 Характеристики газа. Физические характеристики газа выражаются в безразмерной форме через показатели изоэнтропы, коэффициенты сжимаемости и функции сжимаемости.
E.3.4 Отношение удельных объемов. Отношение удельных объемов – это отношение полного удельного объема на входе к полному удельному объему на выходе. Под полным удельным объемом на входе понимают то, что соответствует потоку, входящему в роторную часть. Под полным удельным объемом на выходе понимают результаты расчетов для полных условий на выходе.
где
Е.3.5 Отношение величин расхода. Отношение величин расхода – это отношение численных значений параметра расхода для двух точек, находящихся в потоке. Оно задается выражением
где
w = величина местного массового расхода p = местная полная плотность а x и y обозначают разные точки в границах каскада. Величины расхода, полученные таким образом, имеют размерность объемного расхода, однако не представляют фактический объемный расход, поскольку они были определены в зависимости от условий полной плотности. Делается предположение о том, что существует функциональная зависимость между указанными величинами расхода и фактическими значениями объемного расхода для условий проведения испытаний и для заданных эксплуатационных условий. Предположение является истинным в том случае, когда величины местных чисел Маха текучей среды для условий проведения испытаний и для заданных эксплуатационных условий совпадают, а отклонения считаются пренебрежимо малыми в случае не превышения пределов отклонения числа Маха агрегата в соответствии с данными настоящей Методики.
Е.3.6 Число Маха агрегата. Число Маха агрегата задается следующим выражением:
где U = окружная скорость лопатки рабочего колеса первой ступени или окружная скорость по концевой кромке лопатки ротора первой ступени а = звуковая скорость при полных входных условиях Для идеальных газов
Для реальных газов
Значение числа Маха агрегата, вычисленное таким образом, не является фактическим значением числа Маха текучей среды. Значение числа Маха агрегата практически прямо пропорционально фактическому значению числа Маха текучей среды в тех случаях, когда не превышаются пределы отклонения, заданные в настоящей Методике. Предельные величины отклонений, представленные в Табл. 3.2 и 3.3 для центробежных и осевых компрессоров, также приведены в виде уравнений в Табл. Е.1.
Е.3.7 Число Рейнольдса агрегата. Число Рейнольдса агрегата задается следующим выражением:
Для центробежных компрессоров, b – ширина выходной части рабочего колеса первой ступени в интересующем каскаде. Для осевых компрессоров, b – длина хордыпо концевой кромке лопатки ротора первой ступени. Вязкость u определена для входных условий (условий полного торможения потока). Предельные величины отклонений согласно данным настоящей Методики, представленные в Табл. 3.4 для центробежных компрессоров, также приведены в виде уравнений в Табл. Е.2.
Е.3.8 Коэффициент изоэнтропической работы. Коэффициент изоэнтропической работы задается следующим выражением:
ТАБЛИЦА E.1
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.009 с.) |


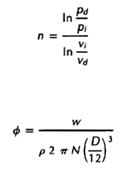



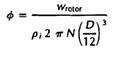





 или
или 





