
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов физическогоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Введение
Представленный практикум является второй частью издания «Медбиофизика. Лабораторный практикум» с общим объемом 18–20 лабораторных работ, разработанный с учетом ФГОС третьего поколения. «Медбиофизика. Лабораторный практикум» включает в себя лабораторные работы с №1 по №9, в данном практикуме содержатся лабораторные работы с №10 по №16. Лабораторный практикум содержит описание лабораторных работ, подготовленных в соответствии с рабочей программой, утвержденной для медицинских ВУЗов. Изложению работ предшествует вводное занятие, посвященное обработке результатов физического и медико-биологического эксперимента, что в дальнейшем поможет студентам произвести расчет в ходе выполнения лабораторных работ. Для облегчения усвоения учебного материала, в практикуме к каждой лабораторной работе изложен теоретический материал в соответствии с программой курса физики для медицинских ВУЗов. Все представленные работы составлены по единому плану и содержат элементы теории и описание установки. Кроме того, приводится порядок выполнения работы, последовательность обработки результатов экспериментальных измерений и вычислений. Практикум позволит изучить основные законы физики, физические явления, а также закономерности, лежащие в основе процессов, протекающих в человеческом организме. Он даст возможность расширения и углубления знаний, умений и навыков для дальнейшего продолжения обучения и успешной профессиональной деятельности. Одновременно с этим он познакомит обучающихся с правилами техники безопасности в физических лабораториях, физическими основами устройств и функционирования медицинской аппаратуры. Практикум научит пользоваться физическим оборудованием и измерительной техникой, производить эксперимент и расчеты по его результатам. Подготовленный практикум поможет студентам лечебного факультета в овладении общекультурными и профессиональными компетенциями. В частности, следующими общекультурными компетенциями: – способности и готовности анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1); – способностью и готовностью к логическому и аргументированному анализу, к публичной речи, ведению дискуссий и полемике, к редактированию текстов профессионального содержания, к осуществлению воспитательной и педагогической деятельности, к сотрудничеству и разрешению конфликтов, к толерантности (ОК-5); а также следующими профессиональными компетенциями: – способностью и готовностью выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, использовать для их решения соответствующих физико-химический и математический аппарат (ПК-2); – способностью и готовностью к формированию системного подхода к анализу медицинской информации, опираясь на всеобъемлющие принципы доказательной медицины, основанной на поиске решений с использованием теоретических знаний и практических умений в целях совершенствования профессиональной деятельности (ПК-3); – способностью и готовностью к работе с медико-технической аппаратурой, используемой в работе с пациентами, владеть компьютерной техникой, получать информацию из различных источников, работать с информацией в глобальных компьютерных сетях, применять возможности современных информационных технологий, для решения профессиональных задач (ПК-9); – способностью, готовностью выполнять основные лечебные мероприятия при наиболее часто встречающихся заболеваниях и состояниях у взрослого населения и подростков, способных вызвать тяжелые осложнения и (или) летальный исход: заболевания нервной, эндокринной, иммунной, сердечно-сосудистой, дыхательной, пищеварительной, мочеполовой систем и крови, своевременно выявлять жизнеопасные нарушения (острая кровопотеря, нарушение дыхания, остановка сердца, кома, шок), использовать методики их немедленного устранения, осуществлять противошоковые мероприятия (ПК-19); – способность и готовность давать рекомендации по выбору оптимального режима двигательной активности в зависимости от морфофункционального статуса, определять показания и противопоказания к назначению средств лечебной физкультуры, физиотерапии, рефлексотерапии, фитотерапии, гомеопатии и других средств немедикаментозной терапии, использовать основные курортные факторы при лечении взрослого населения и подростков (ПК-24); – способностью и готовностью использовать нормативную документацию, принятую в здравоохранении (законы Российской Федерации, технические регламенты, международные и национальные стандарты, приказы, рекомендации, терминологию, международные системы единиц (СИ), действующие международные классификации), а также документацию для оценки качества и эффективности работы медицинских организаций (ПК-27); – способностью и готовностью изучать научно-медицинскую информацию, отечественный и зарубежный опыт по тематике исследования (ПК-31); – способностью и готовностью к участию в освоении современных теоретических и экспериментальных методов исследования, с целью создания новых перспективных средств, в организации работ по практическому использованию и внедрению результатов исследований (ПК-32). Диагностика формирования компетенций обучающихся в процессе изучения учебных дисциплин, междисциплинарных курсов или иных учебных модулей осуществляется посредством проведения текущего, предварительного, рубежного или итогового контроля – контролирующих мероприятий. Последовательность проведения контролирующих мероприятий заключается в планировании, организации и проведении с последующей оценкой результатов контроля как процедуры сопоставления зафиксированных ответов обучающихся с требованиями к решению учебных задач. Проведение контроля предполагает использование контрольных измерительных материалов в соответствии с императивными, дозволительными и рекомендательными нормами, определенными технологией проведения контролирующих мероприятий. Существует несколько методов оценки профессиональных качеств экспертов, которые делят на априорные, апостериорные и тестовые. К априорным методам относят самооценивание, взаимное оценивание и документационный метод. Методы самооценки основаны на использовании балльных, вербально-числовых и вербальных шкал. Апостериорные методы оценки качества экспертов основаны на сравнении отклонений индивидуальных данных от результирующей групповой оценки. С помощью апостериорных методов можно оценить коньюктурность, конформизм и воспроизводимость оценок эксперта. Тестовые методы оценки экспертов основаны на тестировании с целью установления квалификации, навыков и опыта работы эксперта. Оценка качества подготовки студентов будет включать текущий контроль, рубежный контроль и итоговый контроль. Текущий контроль, то есть проверка усвоения учебного материала, регулярно осуществляемая на протяжении семестра, осуществляется в форме устных опросов во время практических занятий. Рубежный контроль осуществляется в виде сдачи коллоквиума. Полученные в результате этого данные служат основой для балльно-рейтинговой оценки успеваемости студента. Итоговый контроль проводится в конце семестра в форме зачета и завершает изучение дисциплины служит для проверки результатов обучения в целом, при этом оценивается совокупность приобретенных студентом общеобразовательных и профессиональных компетенций.
Практическое занятие Краткая теория Введение При экспериментальных исследованиях (в физике, химии, биологии, медицине) часто приходится иметь дело с объектами, свойства которых изменяются случайным образом от опыта к опыту (т.е. во времени) или от объекта к объекту вследствие либо случайной их природы, либо влияния неучтенных причин или случайных погрешностей измерения. Повторяя подряд несколько раз опыты, получают ряд значений исследуемой величины, обычно отличных друг от друга. Возникает вопрос, как по этим данным найти такое приближенное значение (т.е. вычислить такую оценку) неизвестной величины, чтобы погрешность (отличие оценки от истинного ее значения) была бы минимальной. Ответ на этот вопрос дают методы математической статистики. Математическая статистика основана на теории вероятностей, поэтому предварительно перед выполнением этой работы, необходимо ознакомиться с основами теории вероятностей. Математическая статистика решает следующие задачи: вычисление оценок статистических характеристик случайной величины; определение надежности этих оценок; планирование эксперимента до и в ходе исследования. Наиболее часто в практических исследованиях результаты эксперимента оказываются распределенными по так называемому нормальному закону распределения (распределению Гаусса). В частности, нормальный закон распределения имеют вес и размеры животных одного вида, вес и объем мозга, величина артериального давления, температуры, количество эритроцитов в крови и т.п. В данной работе необходимо полученное экспериментально распределение сравнить с теоретическим нормальным распределением.
Пример дискретного вариационного ряда
Строим соответствующий полигон частот.
0.5 0.3
0.2
0.1
1 2 3 4 5 6 7 8 9 10 Xi Рисунок 1.Полигон частот
Полигон используется при графическом представлении дискретных вариационных рядов, когда число вариант невелико (n≤30). Для графического представления интервального вариационного ряда служит гистограмма - ступенчатая фигура, которая состоит из прямоугольников, основаниями которых являются интервалы длиной
Рисунок 2.Гистограмма
Площадь всей гистограммы численно равна суме всех частот ряда, т.е. должна быть равна единице (исходя из условия нормировки):
Интервальный вариационный ряд можно преобразовать в дискретный. Для этого надо вычислить в каждом интервале среднее значение
где Полигон и гистограмма являются приближенными оценками плотности распределения вероятностей. Среднее арифметическое значений вариант характеризует приближенно математическое ожидание случайной величины, т.е. является его оценкой:
Оценка дисперсии. Исправленная дисперсия характеризует рассеивание случайной величины и находится по формуле:
или Дисперсия имеет размерность квадрата измеряемой величины. Чтобы характеризовать рассеивание в тех же единицах, что и измеряемая величина, вычисляют среднее квадратичное отклонение:
Все эти величины необходимо вычислить, т.е. определить характеристики экспериментального распределения заданных х i, а также определить, отличается ли полученная эмпирически оценка плотности распределения от нормального закона. Порядок расчета этих характеристик поясним на примере. По известным данным измерения роста 1000 взрослых мужчин оценим характеристики распределения и сравним его с нормальным. В первой строке таблицы приводятся интервалы роста в сантиметрах, во второй – число мужчин, имеющих рост в пределах этого интервала.
Таблица 2 Распределение роста мужчин
Находим относительную частоту в каждом интервале
Таблица 3
Дискретный вариационный ряд
Строим на миллиметровой бумаге гистограмму:
Находим среднее арифметическое значение и среднее квадратическое отклонение по данным дискретного вариационного ряда:
Вычисляем для каждой границы значения нормированных отклонений:
По этим данным из таблицы интеграла вероятностей определяем теоретические вероятности для каждого интервала по формуле:
Таблица 6
Лабораторная работа №10 Электрокардиография Основные понятия и определения: электрическое поле, диполь, биопотенциалы действия, электрокардиографии, векторкардиоскопия и векторкардиография. Цель работы: Подготовить ЭКГ к работе. Выполнять некоторые проверки правильности функционирования ЭКГ, накладывать электроды и производить запись ЭКГ. Определять амплитуду и длительность зубцов ЭКГ, частоту сердечных сокращений по записанной электрокардиограмме. Краткая теория
Потенциал поля диполя Согласно теории Эйнтховена сердце представляет собой токовый диполь, который расположен в однородной проводящей среде. С физической точки зрения диполь – это система, которая состоит из двух зарядов равных по величине и противоположных по знаку, расположенных друг от друга на расстоянии l. Расстояние l называют плечом диполя (рис. 1)
Основной характеристикой диполя является электрический момент диполя
Вектор Диполь, как система зарядов, создает вокруг себя электрическое поле, которое характеризуется вектором напряженности Потенциал точечного заряда определяется формулой:
Знак потенциала определяется знаком заряда. Найдем уравнение для электрического потенциала, созданного диполем в точке А, удаленной от зарядов соответственно на расстоянии r и r1 (рис. 2).
Рисунок 2. Определение потенциала в точке А.
Потенциал в точке А (φА) складывается из потенциалов, созданных отрицательным и положительным зарядов соответственно, т.е.
При условии, что l<<r и l<<r1, тогда r≈r1, а их произведение r∙r1≈r2. Из рисунка 2 видно, что r–r1≈l∙cosα, где α – угол между вектором При этих условиях получаем Так как Вывод: потенциал в точке А пропорционален электрическому моменту диполя, т.е. Аналогично можно записать потенциал и для точки В равноотстоящей от диполя:
Разность потенциалов для двух точек поля А и В запишется в виде:
Т.е. разность потенциалов Поместим диполь, создающий электрическое поле, в центр равностороннего треугольника АВС (рис. 3)
Рисунок 3. Проекция вектора на стороны равностороннего треугольника
Найдем проекции этого вектора φАВ : φВС : φСА= рАВ: рВС: рСА Теория Эйнтховена для ЭКГ Физические основы ЭКГ заключаются в создании модели электрического генератора, который создавал бы разность потенциалов, соответствующую по величине разности потенциалов между какими-то точками на поверхности тела, созданной сердцем как источником электрического поля. Голландский ученый Эйнтховен предложил теорию ЭКГ, которая используется в медицине по настоящее время (за цикл работ по ЭКГ Эйнтховен в 1924 г удостоен Нобелевской премии). Основные положения теории Эйнтховена: 1. Электрическое поле, созданное сердцем можно представить как поле, созданное токовым диполем с электрическим моментом токового диполя 2. ИЭВС 3. ИЭВС
Рисунок 4. Проекции ИЭВС ( Эйнтховен предложил проектировать петли (проекции
Вершины треугольника условно обозначают ПР (правая рука), ЛР (левая рука), ЛН (левая нога), общая точка ПН (права нога). Стороны треугольника называют линиями отведения. Регистрация разности потенциалов между вершинами треугольника называют регистрацией ЭКГ в стандартных отведениях: I (первое) отведение – разность потенциалов между вершинами ПР и ЛР относительно ПН, II (второе) отведение – ПР-ЛН, III (третье) отведение – ЛР-ЛН (рис. 4). Существует дополнительный электрод Г – грудные отведения V (грудной электрод фиксирует в нескольких точках на поверхности груди, получая соответственно несколько грудных ЭКГ). Электроды при снятии ЭКГ фиксируют не в вершинах равностороннего треугольника, а в эквипотенциальных им точках - обычно в нижних частях соответственно правой руки, левой руки, левой ноги, правой ноги (общий электрод). Примерный вид графической регистрации разности потенциалов II-го отведения показан на рис.5 (L1 – период сердечных сокращений). Зубец “ Р ” соответствует проекции петли “ Р” на II-е отведение, Q – петли Q, R – петли R, S – петли S, Т – петли Т.
Рисунок 5. Зубцы ЭКГ: P, Q, R, S, T
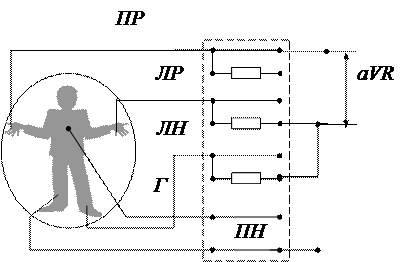
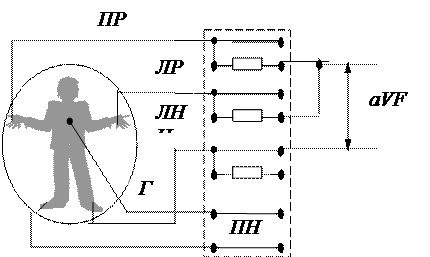
Физиологический смысл зубцов ЭКГ: Зубец “ Р ” отражает возбуждение предсердий. Зубец “ Q” – деполяризация межжелудочковой перегородки (на многих отведениях отсутствует). Зубец “ R ” – деполяризация верхушки, передней, задней и боковой стенки желудочков сердца. Зубец “ S ” – возбуждение основания желудочков сердца. Зубец “ Т ” – реполяризация желудочков сердца. Интервал “ P-Q ” – деполяризация предсердий. Интервал “ Q-T ” – систола желудочков. Интервал комплекса “ QRS ” – деполяризация желудочков. Интервал “ Т-Р ” – состояние “покоя” миокарда. Записанную на бумаге Dj(t) в каком-либо отведении называют электрокардиограммой, а метод регистрации – электрокардиографией. Если разность потенциалов подать на вертикально отклоняющие пластины осциллографа, то на экране получим кривую, аналогичную рис.5. Метод называется электрокардиоскопией. Метод регистрации петель P, QRS, T (рис. 4) путем записи их на бумаге называется векторкардиографией. Если подать разность потенциалов с одного отведения на вертикально отклоняющие пластины, а с другого – на горизонтально отклоняющие пластины электронно-лучевой трубки (осциллографа), то при сложении взаимно перпендикулярных колебаний ЭКГ на экране получатся петли Р, QRS, Т, аналогичные петлям, изображенным на рис.4. Такой метод регистрации называется векторкардиоскопией. Регистрация ЭКГ в каком-либо отведении дает только часть информации о пространственной кривой, описываемой концом - отведение грудного электрода с каждым из стандартных, обозначаемых соответственно CR, CL, CF - (рис.6а); - однополюсные отведения, которые образуются одним из стандартных электродов и средней точкой, полученной путем соединения трех стандартных электродов, каждого последовательно с высокоомным резистором. Наиболее распространено из них грудное (рис.6б); - усиленные отведения – модификация однополюсных, образуемых одним из стандартных электродов и средней точкой, полученной соединением через высокоомный резистор двух других стандартных электродов. Усиленные отведения обозначают как aVR, aVL, aVF (рис. 6 в, г, д).
Рисунок 6. I-е II-е III-е стандартные отведения
а
б Рисунок 6а и 6б. Грудные отведения
в
г
д Рисунок 6в, 6г и 6д. Усиленные отведения Использование ЭВМ Выполнение работы Рисунок 7. Записанная на ЭКГ кривая для оценки Постоянной времени прибора
Упражнение№4. Запись ЭКГ пациента 1. Наложите электроды с использованием прокладок, смоченных физиологическим раствором. 2. Подсоедените кабель отведений к электродам: КРАСНЫЙ - к правой руке, ЖЕЛТЫЙ - к левой руке, ЗЕЛЕНЫЙ - к левой ноге, ЧЕРНЫЙ - к правой ноге (БЕЛЫЙ "грудной" - свободен). 3. Поставьте переключатель отведений в положение " II " (второе отведение). 4. Нажмите кнопку " 50 мм/с " (отжатое положение), переключатель чувсвительности поствьте в положение " 20 мм/мВ ", сместите перо на 10 мм ниже середины ленты. 5. Пациент должен расслабиться, не прикасаться к прибору, после чего нажатием кнопки " М " запишите ЭКГ (4-6 периодов). 6. Поставьте ВСЕ кнопки в отжатое положение, переключатель отведений в положение " 1 mV ", нажатием кнопки выключения питания (слева вверху) выключите ЭКГ, отключите вилку прибора от сети. 7. Определите амплитуду одного из зубцов ЭКГ в мВ по формуле: U=A/H, где, A - амплитуда зубца на ЭКГ в мм, Н - чувствительность прибора в мм/мВ (амплитуда записанного калибровочного импульса в 1-м упражнении). 8. Найдите длительность одного из зубцов ЭКГ по формуле: τ =L/υ, где L - ширина зубца на ЭКГ в мм, 9. Найдите частоту сердечных сокращений данного пациента (число сокращений в минуту) по формуле: n = (60×
R R P T P T
Q S Q S Рисунок 8. Зубцы ЭКГ: P, Q, R, S, T
Контрольные вопросы 1. Определение диполя, электрическое поле диполя (с выводом формулы для разности потенциалов поля диполя). 2. Понятие о биопотенциалах действия. 3. Теорию электрокардиографии, треугольник Эйнтховена. 4. Отведения при электрокардиографии. 5. Структурная схема ЭКГ. 6. Понятие о векторкардиоскопии и векторкардиографии. 7. Методы повышения помехоустойчивости при снятии ЭКГ, дифференциальный усилитель. Назначение и сущность проверок правильности функционирования ЭКГ.
Лабораторная работа №11 Краткая теория Изучение переменных токов имеет большое значение при рассмотрении физиологических процессов в организме человека и животных. Переменные токи нашли большое применение при лечении различных заболеваний. На использовании переменных токов основаны ряд физиотерапевтических методов лечения и диагностики. Переменные токи могут оказывать раздражающее действие на ткани организма. Оно связанно с кратковременным смещением ионов под действием переменного электрического поля, которое также может вызывать изменение концентрации тканевых ионов у клеточных мембран. Раздражающее действие переменного тока в значительной мере зависит от его частоты. С увеличением частоты, когда смещение ионов в направленном движении делается соизмеримым со смещением их при тепловом движении, ток уже не оказывает на ткани раздражающего действия. При этом оказывается тепловое действие тока. Это свойство используется для прогревания тканей организма высокочастотными переменными токами (диатермия). Другими физиотерапевтическими методами, использующими высокочастотные переменные токи, является дарсонвализация – воздействие высокочастотным током в виде разряда, проходящего между специальным электродом и поверхностью кожи больного (аппараты типа «Искра» и др.). По сравнению с постоянным током для сопротивления в цепи переменного тока помимо активной нагрузки имеет большое значение наличие в цепи электроёмкости «С» и индуктивности «L». Сопротивление, которое оказывает электрическая цепь, содержащая компоненты R, L, C, соединённые последовательно называется импедансом и рассчитывается при их последовательном соединении по формуле:
Так как в биологических объектах индуктивность незначительна (L» 0), то формула для расчёта их импеданса принимает вид:
Известно, что активное омическое сопротивление R биологической ткани практически не зависит от частоты тока, а ёмкостное - значительно уменьшается по мере увеличения частоты, что приводит к увеличению проводимости всей емкостно-омической системы. Импеданс тканей организма зависит от их кровенаполнения. На этом основан метод исследования функции кровообращения, называемый реографией. При этом в течение цикла сердечной деятельности регистрируются изменения импеданса определённого участка тканей, на границе которого накладываются электроды.
Рассмотрим наиболее общие законы цепей переменного тока
Рисунок 1. Рисунок 2. Рисунок 3. Подключение в цепь переменного тока сопротивления «R» (рис. 1), индуктивности «L» (рис.2) и конденсатора электроемкостью «С» (рис. 3)
Если к концам проводника с сопротивлением R (рис.1) приложено переменное напряжение, величина которого во времени определяется уравнением
(где
где Из уравнений (1) и (2) видно, что ток и напряжение на активном сопротивлении совпадает по фазе.
2. Рассмотрим цепь переменного тока с индуктивностью L (рис.2) без омического сопротивления (R =0). Тогда в цепи пойдёт ток:
Под действием этого тока в катушке индуктивности возникает э.д.с. самоиндукции:
Для замкнутой цепи, согласно второму правилу Кирхгофа (в замкнутом контуре алгебраически сумма электродвижущих сил равна алгебраической сумме падений напряжений) можно написать:
Тогда:
Вычисляя
Сравнивая уравнения (3) и (5) видим, что напряжение на индуктивности опережает ток на угол Величину индуктивного сопротивления можно определить из уравнения (5) при амплитудном значении напряжения, т.е. при
где
3. Рассмотрим цепь переменного тока с конденсатором ёмкостью C (рис.3). Активная нагрузка в цепи отсутствует | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |














 , а высоты равны отношению
, а высоты равны отношению  (см. рис. 2). Площадь
(см. рис. 2). Площадь  i -го частичного прямоугольника численно равна относительной частоте попадания в интервал
i -го частичного прямоугольника численно равна относительной частоте попадания в интервал  (3)
(3)
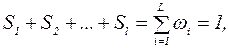 где к =1,2,3,…, L.
где к =1,2,3,…, L. и
и  ;
; 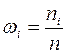 , (4)
, (4) - значения вариант, попавших в i -ый интервал,
- значения вариант, попавших в i -ый интервал,  - количество вариант, попавших в i -ый интервал.
- количество вариант, попавших в i -ый интервал.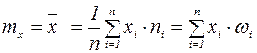 (5)
(5)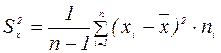 (6)
(6) для n >30 (7)
для n >30 (7) (8)
(8) и записываем полученный интервальный вариационный ряд.
и записываем полученный интервальный вариационный ряд. =
= 

 = 147,5·0.014+156,5·0.211+165,5·0,552+174,5·0.212+183,5·0.014=165,5
= 147,5·0.014+156,5·0.211+165,5·0,552+174,5·0.212+183,5·0.014=165,5 По полученным данным
По полученным данным  =165,5; Sx =6,5 вычисляем теоретические значения вероятностей попадания в каждый интервал. Вероятность равна разности значений интеграла вероятностей для верхней и нижней границ интервала.
=165,5; Sx =6,5 вычисляем теоретические значения вероятностей попадания в каждый интервал. Вероятность равна разности значений интеграла вероятностей для верхней и нижней границ интервала. и
и 



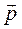 , который определяется как произведение заряда
, который определяется как произведение заряда  на плечо диполя
на плечо диполя  , т.е.
, т.е.
 и потенциалом φ.
и потенциалом φ.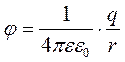

 .
.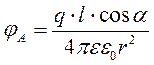 .
.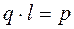 , то
, то 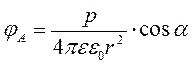 .
. ~
~ 
 (1)
(1) ~
~ 
 т, называемого в электрокардиографии интегральным электрическим вектором сердца (ИЭВС) -
т, называемого в электрокардиографии интегральным электрическим вектором сердца (ИЭВС) -  с.
с.





 =50 мм/с - скорость движения ленты.
=50 мм/с - скорость движения ленты.
 .
. .
.
 (1)
(1) - амплитудное значение напряжения,
- амплитудное значение напряжения,  - круговая частота, равная
- круговая частота, равная 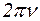 ,
,  - частота тока), то в цепи пойдёт ток, величина которого определяется согласно закону Ома уравнением:
- частота тока), то в цепи пойдёт ток, величина которого определяется согласно закону Ома уравнением: , (2)
, (2) - активное сопротивление,
- активное сопротивление,  - амплитудное значение тока.
- амплитудное значение тока. . (3)
. (3) . (4)
. (4)
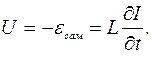
 из уравнения (3)
из уравнения (3)  и, подставляя это значение для нахождения U, имеем:
и, подставляя это значение для нахождения U, имеем: , но
, но 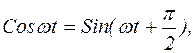 следовательно:
следовательно: (5)
(5) .
. , получим
, получим 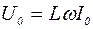 , (6)
, (6)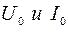 амплитудные значения напряжения и тока. Поделив обе части уравнения (6) на
амплитудные значения напряжения и тока. Поделив обе части уравнения (6) на  , но
, но  - индуктивное сопротивление. Тогда
- индуктивное сопротивление. Тогда  , т.е. величина индуктивного сопротивления прямо пропорциональна от индуктивности катушки и частоте переменного тока.
, т.е. величина индуктивного сопротивления прямо пропорциональна от индуктивности катушки и частоте переменного тока. 0. Приложим к зажимам конденсатора напряжение:
0. Приложим к зажимам конденсатора напряжение:


