
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение импеданса биологического объектаСодержание книги
Поиск на нашем сайте
Основные понятия и определения: основные характеристики переменного тока (мгновенные, амплитудные, эффективные значения напряжения и силы переменного тока, период, частоту и фазу переменного тока); импеданс, реография. Цель работы: работать с электроизмерительными приборами; экспериментально получать зависимости сопротивлений от частоты переменного тока: индуктивного -
Краткая теория Изучение переменных токов имеет большое значение при рассмотрении физиологических процессов в организме человека и животных. Переменные токи нашли большое применение при лечении различных заболеваний. На использовании переменных токов основаны ряд физиотерапевтических методов лечения и диагностики. Переменные токи могут оказывать раздражающее действие на ткани организма. Оно связанно с кратковременным смещением ионов под действием переменного электрического поля, которое также может вызывать изменение концентрации тканевых ионов у клеточных мембран. Раздражающее действие переменного тока в значительной мере зависит от его частоты. С увеличением частоты, когда смещение ионов в направленном движении делается соизмеримым со смещением их при тепловом движении, ток уже не оказывает на ткани раздражающего действия. При этом оказывается тепловое действие тока. Это свойство используется для прогревания тканей организма высокочастотными переменными токами (диатермия). Другими физиотерапевтическими методами, использующими высокочастотные переменные токи, является дарсонвализация – воздействие высокочастотным током в виде разряда, проходящего между специальным электродом и поверхностью кожи больного (аппараты типа «Искра» и др.). По сравнению с постоянным током для сопротивления в цепи переменного тока помимо активной нагрузки имеет большое значение наличие в цепи электроёмкости «С» и индуктивности «L». Сопротивление, которое оказывает электрическая цепь, содержащая компоненты R, L, C, соединённые последовательно называется импедансом и рассчитывается при их последовательном соединении по формуле:
Так как в биологических объектах индуктивность незначительна (L» 0), то формула для расчёта их импеданса принимает вид:
Известно, что активное омическое сопротивление R биологической ткани практически не зависит от частоты тока, а ёмкостное - значительно уменьшается по мере увеличения частоты, что приводит к увеличению проводимости всей емкостно-омической системы. Импеданс тканей организма зависит от их кровенаполнения. На этом основан метод исследования функции кровообращения, называемый реографией. При этом в течение цикла сердечной деятельности регистрируются изменения импеданса определённого участка тканей, на границе которого накладываются электроды.
Рассмотрим наиболее общие законы цепей переменного тока
Рисунок 1. Рисунок 2. Рисунок 3. Подключение в цепь переменного тока сопротивления «R» (рис. 1), индуктивности «L» (рис.2) и конденсатора электроемкостью «С» (рис. 3)
Если к концам проводника с сопротивлением R (рис.1) приложено переменное напряжение, величина которого во времени определяется уравнением
(где
где Из уравнений (1) и (2) видно, что ток и напряжение на активном сопротивлении совпадает по фазе.
2. Рассмотрим цепь переменного тока с индуктивностью L (рис.2) без омического сопротивления (R =0). Тогда в цепи пойдёт ток:
Под действием этого тока в катушке индуктивности возникает э.д.с. самоиндукции:
Для замкнутой цепи, согласно второму правилу Кирхгофа (в замкнутом контуре алгебраически сумма электродвижущих сил равна алгебраической сумме падений напряжений) можно написать:
Тогда:
Вычисляя
Сравнивая уравнения (3) и (5) видим, что напряжение на индуктивности опережает ток на угол Величину индуктивного сопротивления можно определить из уравнения (5) при амплитудном значении напряжения, т.е. при
где
3. Рассмотрим цепь переменного тока с конденсатором ёмкостью C (рис.3). Активная нагрузка в цепи отсутствует
Обкладки конденсора получают заряд, изменяющийся пропорционально напряжению:
В цепи конденсатора пойдёт ток, величина которого равна скорости изменения заряда конденсатора или пропорциональна скорости изменения напряжения на его зажимах.
Получим закон изменения тока в конденсаторе. Для этого найдем
Подставляя в уравнение (10) значение
Сравнивая уравнения (12) и (8) видим, что ток опережает напряжение на конденсаторе на угол Найдем величину ёмкостного сопротивления из уравнения (12). При амплитудном значении тока, когда
Так как
т.е. ёмкостное сопротивление обратно пропорционально ёмкости конденсатора и частоте переменного тока. 4. Реальные цепи переменного тока содержат все три компонента: R, L и C. Рассмотрим такую цепь при последовательном соединении (рис. 4). Напряжение
Рисунок 4. Последовательно соединенные R, L и C подключены к переменному напряжению
Для определения угла сдвига фаз Для построения векторной диаграммы отложим по горизонтальной оси вектор тока, равный по величине амплитудному значению I0 (рис. 5). Тогда мгновенное значение силы тока Так как на активном сопротивлении вектор тока совпадает с вектором напряжении по фазе, то Для нахождения результирующего вектора напряжения
где:
Рисунок 5. Векторная диаграмма тока
Подставляя эти (16, 17 и 18) значения
Известно, что многие приборы измеряют эффективные значения тока и напряжения
Каждое из соотношений (19) и (20) выражает обобщенный закон Ома для цепи переменного тока при последовательном соединении R, L и C, где
называют импедансом цепи. Угол сдвига фаз между током
|
|||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.45.159 (0.01 с.) |

 , емкостного -
, емкостного -  , биологической ткани -
, биологической ткани -  ; производить соответствующие расчеты и по графику функциональной зависимости импеданса биообъекта от частоты переменного тока оценивать его активное сопротивление.
; производить соответствующие расчеты и по графику функциональной зависимости импеданса биообъекта от частоты переменного тока оценивать его активное сопротивление. .
. .
.
 (1)
(1) - амплитудное значение напряжения,
- амплитудное значение напряжения,  - круговая частота, равная
- круговая частота, равная 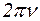 ,
,  - частота тока), то в цепи пойдёт ток, величина которого определяется согласно закону Ома уравнением:
- частота тока), то в цепи пойдёт ток, величина которого определяется согласно закону Ома уравнением: , (2)
, (2) - активное сопротивление,
- активное сопротивление,  - амплитудное значение тока.
- амплитудное значение тока. . (3)
. (3) . (4)
. (4)
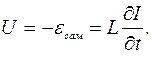
 из уравнения (3)
из уравнения (3)  и, подставляя это значение для нахождения U, имеем:
и, подставляя это значение для нахождения U, имеем: , но
, но 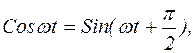 следовательно:
следовательно: (5)
(5) .
. , получим
, получим 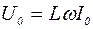 , (6)
, (6)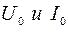 амплитудные значения напряжения и тока. Поделив обе части уравнения (6) на
амплитудные значения напряжения и тока. Поделив обе части уравнения (6) на  , но
, но  - индуктивное сопротивление. Тогда
- индуктивное сопротивление. Тогда  , т.е. величина индуктивного сопротивления прямо пропорциональна от индуктивности катушки и частоте переменного тока.
, т.е. величина индуктивного сопротивления прямо пропорциональна от индуктивности катушки и частоте переменного тока. 0. Приложим к зажимам конденсатора напряжение:
0. Приложим к зажимам конденсатора напряжение: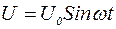 . (8)
. (8) . (9)
. (9) . (10)
. (10) из уравнения (8):
из уравнения (8): (11)
(11)
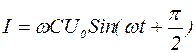 . (12)
. (12) будем иметь:
будем иметь: . (13)
. (13) , то, поделив уравнения (13) на
, то, поделив уравнения (13) на  , получим выражение для величины ёмкостного сопротивления:
, получим выражение для величины ёмкостного сопротивления: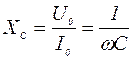 . (14)
. (14) вызывает ток
вызывает ток  , где
, где  - сдвиг фаз между током и напряжением, причем +
- сдвиг фаз между током и напряжением, причем +  в том случае, когда
в том случае, когда  > XC, а -
> XC, а - 
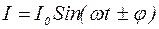 будет равно проекции этого вектора, вращающегося против часовой стрелки с угловой скоростью
будет равно проекции этого вектора, вращающегося против часовой стрелки с угловой скоростью 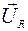 отложится по той же оси, что и ток
отложится по той же оси, что и ток  . На индуктивности напряжение
. На индуктивности напряжение 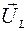 опережает ток по фазе на
опережает ток по фазе на  отстает по фазе от тока на угол
отстает по фазе от тока на угол  векторно (геометрически) складывают вектора
векторно (геометрически) складывают вектора  . Так как
. Так как  направленный в сторону большого по модулю вектора. Затем вектор
направленный в сторону большого по модулю вектора. Затем вектор  складываем по правилу параллелограмма с вектором
складываем по правилу параллелограмма с вектором  . Из прямоугольного треугольника 0АВ по теореме Пифагора имеем:
. Из прямоугольного треугольника 0АВ по теореме Пифагора имеем: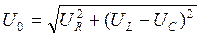 , (15)
, (15) , (16)
, (16) , (17)
, (17) . (18)
. (18)
 ,
,  ,
,  и
и  при последовательном соединении R, L и C и при UL>UC (XL>XC)
при последовательном соединении R, L и C и при UL>UC (XL>XC) ,
,  ,
,  в уравнение (15), получаем:
в уравнение (15), получаем:  , откуда
, откуда . (19)
. (19) и
и  . Они связаны для их гармонических колебаний с максимальными значениями как:
. Они связаны для их гармонических колебаний с максимальными значениями как:  ,
,  . Заменяя в формуле (19) максимальные значения
. Заменяя в формуле (19) максимальные значения  и
и  . (20)
. (20) (21)
(21) . (22)
. (22)


