
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика оценки статистических характеристикСодержание книги
Поиск на нашем сайте
В результате эксперимента, обычно, получают совокупность результатов, называемых в статистике вариантами: x1, x2, x3,…,xn. Если варианты расположить упорядоченно (в порядке возрастания или убывания), то получается последовательность, называемая дискретным вариационным рядом x1, x2, x3,…,xn. Каждой варианте такого ряда ставится в соответствие ее частота или число ее появлений ni, и относительная частота
При большом числе испытаний относительную частоту считают приближенно равной статистической вероятности
Если вариант много, то их группируют в интервалы и для каждого интервала вычисляют частоту попадания в него. Такой ряд называют интервальным вариационным рядом. В общем случае, ширина этих интервалов может быть различной, но часто интервалы удобно брать одинаковыми, равными по ширине
где L - число интервалов, определяемое по формуле: L=1+3,32lg n. Статистическое распределение считается полностью заданным, если указаны последовательность вариант (или интервалов) и соответствующих им относительных частот. Полигоном частот называется ломаная, отрезки которой соединяют точки с координатами (xi , Например, дан дискретный вариационный ряд из 20 вариант, представленный в виде табл. 1, где ni – частота появления вариант, Таблица 1 Пример дискретного вариационного ряда
Строим соответствующий полигон частот.
0.5 0.3
0.2
0.1
1 2 3 4 5 6 7 8 9 10 Xi Рисунок 1.Полигон частот
Полигон используется при графическом представлении дискретных вариационных рядов, когда число вариант невелико (n≤30). Для графического представления интервального вариационного ряда служит гистограмма - ступенчатая фигура, которая состоит из прямоугольников, основаниями которых являются интервалы длиной
Рисунок 2.Гистограмма
Площадь всей гистограммы численно равна суме всех частот ряда, т.е. должна быть равна единице (исходя из условия нормировки):
Интервальный вариационный ряд можно преобразовать в дискретный. Для этого надо вычислить в каждом интервале среднее значение
где Полигон и гистограмма являются приближенными оценками плотности распределения вероятностей. Среднее арифметическое значений вариант характеризует приближенно математическое ожидание случайной величины, т.е. является его оценкой:
Оценка дисперсии. Исправленная дисперсия характеризует рассеивание случайной величины и находится по формуле:
или Дисперсия имеет размерность квадрата измеряемой величины. Чтобы характеризовать рассеивание в тех же единицах, что и измеряемая величина, вычисляют среднее квадратичное отклонение:
Все эти величины необходимо вычислить, т.е. определить характеристики экспериментального распределения заданных х i, а также определить, отличается ли полученная эмпирически оценка плотности распределения от нормального закона. Порядок расчета этих характеристик поясним на примере. По известным данным измерения роста 1000 взрослых мужчин оценим характеристики распределения и сравним его с нормальным. В первой строке таблицы приводятся интервалы роста в сантиметрах, во второй – число мужчин, имеющих рост в пределах этого интервала.
Таблица 2 Распределение роста мужчин
Находим относительную частоту в каждом интервале
Таблица 3
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.253.21 (0.006 с.) |

 , равная отношению частоты ni к общему числу вариант:
, равная отношению частоты ni к общему числу вариант: (1)
(1) .
. :
: ,
, ). По оси абсцисс откладывают значения вариант xi, а по оси ординат – соответствующие им относительные частоты
). По оси абсцисс откладывают значения вариант xi, а по оси ординат – соответствующие им относительные частоты 











 , а высоты равны отношению
, а высоты равны отношению  (см. рис. 2). Площадь
(см. рис. 2). Площадь  i -го частичного прямоугольника численно равна относительной частоте попадания в интервал
i -го частичного прямоугольника численно равна относительной частоте попадания в интервал  (3)
(3)
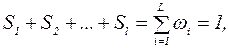 где к =1,2,3,…, L.
где к =1,2,3,…, L. и
и  ;
; 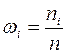 , (4)
, (4) - значения вариант, попавших в i -ый интервал,
- значения вариант, попавших в i -ый интервал,  - количество вариант, попавших в i -ый интервал.
- количество вариант, попавших в i -ый интервал.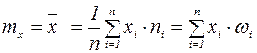 (5)
(5)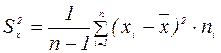 (6)
(6) для n >30 (7)
для n >30 (7) (8)
(8) и записываем полученный интервальный вариационный ряд.
и записываем полученный интервальный вариационный ряд.


