
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок елементів прямокутного профілюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Розглянемо переріз прямокутного профілю (рис. 5.7), заармований звичайною арматурою тільки в розтягнутій зоні (прямокутний переріз з одиничною арматурою). Для цього перерізу На основі (5.1) можна записати:
Умова міцності за (5.2):
Запишемо також умову міцності відносно осі II–II:
Формули (5.4)...(5.6) справедливі при
Рис. 5.7. Прямокутний переріз з одиничною арматурою та схема зусиль при розрахунку на міцність за нормальними перерізами: II–II – вісь, яка нормальна до площини згину і проходить через точку прикладання рівнодійної в стиснутій зоні. Інші позначення дивись до рис. 5.6, б
З рівняння (5.4):
або де m – коефіцієнт армування; З рівняння (5.8) отримаємо:
Максимальний вміст арматури при одиночному армуванні перерізу, коли
Максимальний відсоток армування елементів, що працюють на згинання, збільшується з підвищенням міцності бетону і зменшується з підвищенням міцності сталі. При Максимальні відсотки армування залізобетонних елементів, що працюють на згинання, при бетоні класів В12,5...В30 і сталях А–ІІ, А–ІІІ і Вр–І становлять 1,3...3,2%. З умови мінімальної вартості конструкцій оптимальні відсотки армування і відповідні їм значення відносної висоти стиснутої зони приймають: для балок m% = 0,5...0,6mmax%; m% = 1...2%;x = 0,3...0,5; для плит m% = 0,2...0,3mmax%; m% = 0,3...0,6%; x = 0,1...0,2. Мінімальний відсоток армування для елементів, що працюють на згинання, становить 0,05%. На практиці для розрахунку елементів прямокутного профілю з одиничною арматурою використовують таблиці. Перетворимо рівняння (5.5) так:
Позначимо
Отже, З рівняння (5.4)
де Для коефіцієнтів am, x та z складено таблицю, де за одним відомим коефіцієнтом можна визначити два інших. Отже, маючи значення згинального моменту в перерізі, розміри перерізу і задані класи бетону та арматури за формулою (5.12) визначають коефіцієнт am; із таблиці визначають відповідні йому коефіцієнти x та z. Перевіряють умову x£xR і за формулою
визначають необхідну площу поперечного перерізу арматури. З рівняння (5.12) можна визначити робочу висоту перерізу
Якщо при розрахунках за формулами (5.4)...(5.6) умова Розрахунок елементів таврового профілю
Тавровий профіль (рис. 5.8) у порівнянні з прямокутним перерізом, ширина якого дорівнює ширині полиці, має практично однакову несучу здатність, але значно меншу витрату бетону у зв’язку з меншими розмірами перерізу у розтягнутій зоні. Таврові перерізи з полицею в розтягнутій зоні застосовують значно рідше, бо у цьому разі полиця не підвищує несучої здатності залізобетонного елемента. Такі перерізи розраховують як прямокутні, ширина яких дорівнює ширині ребра. При розрахунку таврових перерізів можливі два випадки: 1 – нейтральна вісь пересікає полицю (рис. 5.8 а); 2 – нейтральна вісь пересікає ребро (рис. 5.8 в). Розмежовують їх так. Визначають момент, що сприймає переріз при повністю стиснутій полиці
Якщо момент від зовнішнього навантаження М£
Рис. 5.8. До розрахунку елементів таврового, довотавровго та коробчастого перерізів: а – перший випадок розрахунку таврового перерізу; б – розрахунковий переріз для першого випадку; в – другий випадок розрахунку таврового перерізу; г – розрахункові перерізи для другого випадку; д – дійсний та розрахунковий двотавровий переріз; е – дійсний та розрахунковий коробчастий переріз Коли ж момент
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 .
. . (5.4)
. (5.4) . (5.5)
. (5.5)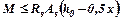 . (5.6)
. (5.6) .
.
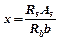 , (5.7)
, (5.7)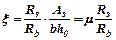 , (5.8)
, (5.8) , або
, або  – відсоток армування.
– відсоток армування.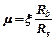 . (5.9)
. (5.9) , обчислюють за формулою
, обчислюють за формулою . (5.10)
. (5.10) , що відповідає
, що відповідає  , переріз переармований.
, переріз переармований. .
. ;
; (5.11)
(5.11) . (5.12)
. (5.12) (5.13)
(5.13) . (5.14)
. (5.14) (5.15)
(5.15) . (5.16)
. (5.16) (5.17)
(5.17)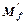 – нейтральна вісь перетинає полицю і тавровий переріз розраховують як прямокутний з шириною b рівною ширині полиці
– нейтральна вісь перетинає полицю і тавровий переріз розраховують як прямокутний з шириною b рівною ширині полиці  за формулами п. 5.3 (рис. 5.8. б).
за формулами п. 5.3 (рис. 5.8. б).
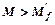 – нейтральна вісь перетинає ребро і тавровий переріз (рис. 5.8, в) поділяють на два прямокутних (рис. 5.8, г). Площу арматури As1 обчислюють як для прямокутного перерізу шириною
– нейтральна вісь перетинає ребро і тавровий переріз (рис. 5.8, в) поділяють на два прямокутних (рис. 5.8, г). Площу арматури As1 обчислюють як для прямокутного перерізу шириною  та висотою h, а площу арматури As2 як для прямокутного перерізу шириною b і висотою h (h – висота таврового перерізу). Повна площа арматури
та висотою h, а площу арматури As2 як для прямокутного перерізу шириною b і висотою h (h – висота таврового перерізу). Повна площа арматури  .
.


