
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи розрахунку залізобетонних конструкційСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Існують три методи розрахунку ЗБК – за допустимими напруженнями, за руйнівними зусиллями та за граничними станами. Про суть розрахунку за першими двома методами див. п.3 вступу. Згідно з діючими нормами проектування, ЗБК розраховують за третім методом – за методом граничних станів. В основу цього методу покладено наступне: – введено поняття граничного стану конструкції і встановлено дві групи граничних станів (перша – за втратою несучої здатності, стійкості або витривалості; друга – за придатністю до нормальної експлуатації); – розрахунок міцності перерізів виконують на стадії руйнування (ІІІ стадія н.д.с.); при цьому епюру напружень у стиснутій зоні бетону приймають прямокутною; – в розрахунки вводиться система коефіцієнтів надійності – щодо навантаження, матеріалів, умов роботи. Граничними називають такі стани, за яких конструкція більше не задовольняє заданих умов нормальної експлуатації. Завдання розрахунку полягає в тому, щоб не допустити за весь період експлуатації конструкції виникнення будь-якого граничного стану. Розрахунок за першою групою граничних станів виконують, щоб запобігти руйнуванню конструкції (розрахунок на міцність), втрати стійкості форми або положення, руйнуванню від утомленості (розрахунок на витривалість), руйнуванню від спільної дії силових факторів і несприятливих впливів зовнішнього середовища. Розрахунок за другою групою граничних станів виконують, щоб запобігти розвиткові недопустимих деформацій (прогинів, кутів повороту та коливань), утворення тріщин або їх надмірного розкриття. За першою групою граничних станів розраховують усі конструкції, а за другою розрахунок виконують тільки у випадках, коли такі стани можуть виникнути. Розрахунок за граничними станами виконують не тільки в стадії експлуатації, а й у стадіях виготовлення, монтажу і транспортування конструкцій. Виникнення граничного стану конструкції залежить від ряду факторів: навантажень, міцнісних характеристик матеріалів та умов роботи. Ці фактори можуть змінюватися у певних межах. Нормативні і розрахункові навантаження. Навантаження поділяються на постійні і тимчасові (довго– та короткочасні і особливі). Конструкції розраховують на невигідні, але реально можливі комбінації навантажень. Розрізняють нормативні і розрахункові навантаження. Нормативні навантаження встановлені нормами, а розрахункові визначаються із залежності Нормативні навантаження від маси конструкції визначаються її об’ємом і середньою густиною матеріалу. Проте фактичні розміри конструкції можуть бути збільшені або зменшені. Змінюється також густина матеріалу. Якщо відхилення фактичної густини матеріалу конструкції не перевищує 10%, то в розрахунок вводять коефіцієнт надійності щодо навантаження, який дорівнює 1,1. Відхилення густини утеплювача від середнього значення і можливість його зволоження враховують коефіцієнтом gf, який дорівнює 1,2 або 1,3. Снігові та вітрові нормативні навантаження визначаються за даними довгострокових метеорологічних спостережень. Для снігових навантажень коефіцієнт gf =1,4...1,6, а для вітрових – 1,2. Нормативне навантаження на перекриття громадських будівель від скупчення людей прийнято за 4 кН/м2. При цьому виходять з припущення, що на 1 м2 перекриття можуть розміститися 5 чол. масою по 80 кг кожен. Однак цілком імовірно, що маса людини може перевищувати 80 кг. Тому вводять коефіцієнт надійності щодо навантаження gf =1,2, і розрахункове навантаження на перекриття вважають за 4,8 кН/м2. Крім того, згідно з правилом урахування ступеня відповідальності будівель і споруд, під час проектування конструкцій до розрахунку вводять коефіцієнти надійності щодо призначення конструкцій, які враховують ступінь відповідальності і капітальності будівель та споруд. Їх приймають меншими чи рівними за одиницю (для більшості будівель та споруд gn =0,95). Нормативні і розрахункові міцності матеріалів. У випробуваннях великої кількості зразків міцнісні характеристики різних матеріалів значною мірою різняться одна від одної. Тому, щоб мати надійні і достовірні характеристики міцності матеріалів, використовують методи математичної статистики.
Рис 4.2. Криві розподілу міцності бетону: 1 – дослідна статистична; 2 – теоретична
Бетон. Під час випробування кубів із бетону дістають різні значення його міцності. Для оцінки розкиду міцнісних характеристик бетону будують криву розподілу його міцності. Зразки групують за міцністю. По осі абсцис відкладають її усереднені значення, а по осі ординат – кількість зразків n, які показали приблизно однакову міцність (рис. 4.2). При досить великій кількості зразків ця крива близька до теоретичної кривої нормального розподілу (кривої Гаусса). Клас бетону В – основна характеристика бетону на стискання. Його значення визначається гарантованим тимчасовим опором на стискання у МПа (з довірчою ймовірністю 95%), який визначають випробуванням еталонних кубів розміром 150х150х150 мм згідно з вимогами державних стандартів. Для визначення класу бетону за результатами випробування зразків обчислюють середній тимчасовий опір бетону, що називають у статистиці математичним сподіванням
Для середнього тимчасового опору бетону довірча імовірність становить 50%. Обчислюють середньоквадратичне відхилення або стандарт
де Як клас бетону приймають величину
де c – число стандартів. У нормах прийнято для бетонів число стандартів c =1,64, що відповідає довірчій імовірності 95%. Формулу (4.3) можна записати у вигляді
де u=s/Rm – коефіцієнт варіації міцності або коефіцієнт мінливості. Обробка результатів численних випробувань кубів на заводах збірного залізобетону показала, що для важких бетонів середнє значення коефіцієнта мінливості можна прийняти за u=0,135. Тоді клас бетону буде: при стисканні при розтяганні У розрахунку використовують нормативну призмову міцність, яка більше відповідає умовам роботи бетону в конструкціях
Розрахунковий опір бетону обчислюють, поділивши нормативний опір на коефіцієнт надійності для бетону gbc або gbt, які враховують можливі відхилення міцності бетону безпосередньо в конструкціях. У розрахунках за граничними станами першої групи: при стисканні де gbc =1,3; при розтяганні де gb t=1,5. У розрахунках за граничними станами другої групи коефіцієнт надійності щодо бетону Арматура. Для арматурних сталей як нормативний опір Rsn приймають найменші контрольовані значення, встановлювані діючими стандартами і перевірені заводськими лабораторіями: –для стержньової арматури класів А–І, А–ІІ, А–ІІІ, що мають площинку текучості, Rsn дорівнює фізичній межі текучості sy з довірчою імовірністю не менш як 0,95; –для стержньової арматури з твердої сталі класів А–IV...Aт–VI, високоміцного дроту класів В–ІІ та Вр–ІІ і арматурних канатів Rsn дорівнює умовній межі текучості s0,2, тобто напруження, яке відповідає залишковому відносному видовженню 0,2%, з тією ж імовірністю; –для звичайного арматурного дроту Rsn дорівнює напруженню, яке відповідає 0,75 тимчасового опору розриву. Розрахункові опори арматури визначають, як і для бетону, діленням нормативного опору на коефіцієнт надійності щодо арматури gs
Коефіцієнти надійності для арматури враховують можливе зменшення площі поперечного перерізу стержнів при мінусовому допуску, можливість зміни механічних властивостей сталі у процесі виготовлення конструкцій та експлуатації їх, недостатній розвиток пластичних деформацій перед розривом для деяких класів арматури. Для арматури класів А–І та А–ІІ коефіцієнт надійності Розрахункові опори арматури розтяганню в розрахунках за граничними станами другої групи приймають з коефіцієнтом надійності gs =1, тобто рівним нормативним: Розрахункові опори арматури стисканню визначають з урахуванням її міцності і граничної деформативності бетону при стисканні в момент його руйнування (див. п. 1.15). Розрахунковий опір арматури під час стискання дорівнює розрахунковому опору під час розтягання Rs, але не більш ніж У разі тривалої дії навантаження повзучість збільшує граничну стискуваність бетону і спричиняє перерозподіл напружень між арматурою та бетоном, довантажуючи арматуру. Тому в ряді випадків розрахунковий опір арматури стисканню Rsc можна приймати рівним 450 і навіть 500 МПа. Коефіцієнт умов роботи. У розрахунках конструкцій за граничними станами вводять ряд коефіцієнтів умов роботи gb та gs. Вони враховують особливості роботи бетону та арматури в залізобетонних конструкціях, вплив технології виготовлення арматурних каркасів, бетонування конструкцій, розміщення арматури в залізобетонних елементах, характер діючих навантажень, фактори, не враховані статичним розрахунком. Встановлено, наприклад, що під дією тривалого навантаження бетон може руйнуватися при нижчих напруженнях, ніж при короткочасному навантаженні. Цей фактор враховується множенням розрахункових опорів бетону Rb та Rbt на коефіцієнт умов роботи бетону gb2 = 0,9. При бетонуванні стиснутих конструкцій у вертикальному положенні при висоті шару бетону понад 1,5 м розрахунковий опір бетону Rb множать на коефіцієнт умов роботи gb3 = 0,85. У розрахунок міцності похилих перерізів для відігнутої і поперечної арматури вводять коефіцієнт умов роботи gs1 = 0,8, який враховує нерівномірний розподіл напружень в арматурі по висоті похилого перерізу, оскільки в момент руйнування не вся арматура, що перетинає тріщину, досягає межі текучості. Зниження пластичних властивостей сталі при точковому зварюванні поперечних стержнів враховують за допомогою коефіцієнта умов роботи gs2 = 0,9. Суть розрахунку конструкцій за граничними станами. При розрахунку за першою групою граничних станів має виконуватися нерівність F £ Fult. (4.10) У лівій частині нерівності подане розрахункове зусилля F від зовнішнього навантаження, що є максимальним у перерізі елемента при найневигіднішій комбінації розрахункових навантажень або діянь. Воно залежить від нормативного навантаження Fn, коефіцієнта надійності щодо навантаження gf і коефіцієнта надійності щодо призначення gn. У правій частині нерівності Fult – внутрішнє граничне зусилля у тому самому перерізі, що є функцією несучої здатності елемента, яка залежить від геометрії перерізу та інших факторів, нормативних опорів матеріалів Rbn та Rsn, їхніх коефіцієнтів надійності для матеріалу gb та gs і умов роботи gbi та gsi. При розрахунку за другою групою граничних станів мають виконуватися нерівності: – на утворення тріщин в розтягнутих елементах Nr £ Ncrc; – те саме, в елементах, що працюють на згинання Mr £ Mcrc; – на розкриття тріщин аcrc £ [acrc]; – на жорсткість f £ [ftot]. У вище наведених нерівностях прийнято такі позначення: Nr та Mr – розрахункові зусилля, а Ncrc та Mcrc – зусилля, що їх сприймає переріз і які визначаються розрахунковим опором матеріалів; acrc та [acrc] – максимальна та гранично допустима ширина розкриття тріщин: f та [ftot] – максимальний та гранично допустимий прогини. Розрахунки за першою і другою групою граничних станів виконують для всіх стадій – виготовлення, транспортування, зведення та експлуатації.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 766; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , де gn – нормативне навантаження; gf – коефіцієнт надійності щодо навантаження; y – коефіцієнт сполучення.
, де gn – нормативне навантаження; gf – коефіцієнт надійності щодо навантаження; y – коефіцієнт сполучення.
 . (4.1)
. (4.1) , (4.2)
, (4.2) ;
; 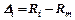 .
. , (4.3)
, (4.3) , (4.4)
, (4.4) ;
; . (4.5)
. (4.5) . (4.6)
. (4.6) , (4.7)
, (4.7) , (4.8)
, (4.8) . У цьому випадку розрахункові опори бетону дорівнюють його нормативним значенням:
. У цьому випадку розрахункові опори бетону дорівнюють його нормативним значенням:  при стисканні і
при стисканні і  при розтяганні. Індекс ser означає, що прийнято гарантовану сертифікаційну міцність.
при розтяганні. Індекс ser означає, що прийнято гарантовану сертифікаційну міцність. . (4.9)
. (4.9) =1,05, для класу А–ІІІ залежно від діаметра gs =1,1 та gs =1,07. Для решти класів стержньової арматури gs =1,15...1,2. Коефіцієнт надійності для високоміцної дротяної арматури та канатів з цього дроту gs =1,2.
=1,05, для класу А–ІІІ залежно від діаметра gs =1,1 та gs =1,07. Для решти класів стержньової арматури gs =1,15...1,2. Коефіцієнт надійності для високоміцної дротяної арматури та канатів з цього дроту gs =1,2. .
. МПа.
МПа.


