Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства действий над векторамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Операции сложения векторов и умножения вектора на число обладают след. свойствами: 1) 2) 3) 4) 5) 6) 7) 8) Выражение координат вектора через координаты его начала и конца. Расстояние между двумя точками. Деление отрезка в данном отношении. Координаты середины отрезка. Расстояние d между точками A(x1) и B(x2) на оси:
Расстояние d между точками A(x1, y1) и B(x2, y2) плоскости определяется по формуле:
Деление отрезка в данном отношении. Если x 1 и y 1 - координаты точки A, а x 2 и y 2 - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении
Если
10. Скалярное произведение векторов. Геометрические свойства скалярного произведения, угол между векторами. Условия ортогональности векторов. Алгебраические свойства скалярного произведения. Выражение скаляроного произведения через координаты множителей. Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Скалярным произведением в векторном пространстве 1. для любых трех элементов 2. для любых 3. для любого Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.
§ Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):
Векторное произведение векторов. Геометрические приложения векторного произведения. Условие коллинеарности векторов. Алгебраические свойства смешанного произведения. Выражение векторного произведения через координаты множителей. Векторным произведением вектора а на вектор b называется вектор с, который: 1. Перпендикулярен векторам a и b, т. е. с^а и с^b; 2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е. 3.Векторы a, b и с образуют правую тройку. Геометрические приложения: Установление коллинеарности векторов
Нахождение площади параллелограмма и треугольника Согласно определению векторного произведения векторов а и b |а хb | = |а| * |b |sing, т. е. S пар = |а х b |. И, значит, DS =1/2|а х b |. Определение момента силы относительно точки Из физики известно, что моментом силы F относительно точки О называется вектор М, который проходит через точку О и: 1) перпендикулярен плоскости, проходящей через точки О, А, В; 2) численно равен произведению силы на плечо
Стало быть, М=ОА х F. Нахождение линейной скорости вращения Скорость v точки М твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется формулой Эйлера v =w хr, где r =ОМ, где О—некоторая неподвижная точка оси (см. рис. 21). Условие коллинеарности векторов - необходимым и достаточным условием коллинеарности ненулевого вектора Алгебраические свойства смешанного произведения Смешанное произведение векторов не изменяется при круговой перестановке сомножителей и изменяет знак на противоположный при перестановке двух сомножителей, сохраняя при этом свой модуль. Знак " Смешанное произведение дистрибутивно относительно любого его сомножителя: (например) если Выражение векторного произведения через координаты
12. Смешанное произведение векторов. Геометрический смысл смешанного произведения, условие компланарности векторов. Алгебраические свойства смешанного произведения. Выражение смешанного произведения через координаты множителей. Смешанным произведением упорядоченной тройки векторов (a,b,c) называется скалярное произведение первого вектора на векторное произведение второго вектора на третий.
Алгебраические свойства векторного произведения -антикоммутативность -ассоциативности относительно умножения на скаляр -дистрибутивности по сложению -тождество Якоби. Выполняется в R3 и нарушается в R7
Векторные произведения базисных векторов находятся по определению
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.231.197 (0.01 с.) |

 ,
, ,
, ,
, ,
,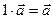 ,
,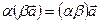 ,
,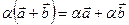 ,
, .
.

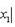





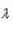
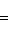
 , определяются по формулам
, определяются по формулам







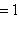 , то точка C (x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам
, то точка C (x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам






 над полем
над полем  называется функция
называется функция 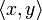 для элементов
для элементов 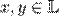 , принимающая значения в
, принимающая значения в  и
и  пространства
пространства 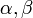 справедливо равенство
справедливо равенство 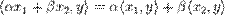 (линейность скалярного произведения по первому аргументу);
(линейность скалярного произведения по первому аргументу); и
и  , где черта означает комплексное сопряжение (эрмитова симметричность);
, где черта означает комплексное сопряжение (эрмитова симметричность); , причем
, причем  только при
только при 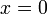 (положительная определенность скалярного произведения).
(положительная определенность скалярного произведения). действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.
действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.



 3) образует правую тройку с векторами ОА и A В.
3) образует правую тройку с векторами ОА и A В. и вектора
и вектора  является существование такого числа
является существование такого числа 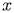 , которое удовлетворяет равенству
, которое удовлетворяет равенству  .
. " векторного умножения внутри смешанного произведения может быть поставлен между любыми его сомножителями.
" векторного умножения внутри смешанного произведения может быть поставлен между любыми его сомножителями. система координат правая
система координат правая система координат левая
система координат левая