
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой в отрезках. Нормальное уравнение прямой на плоскости. Расстояние от точки до данной прямой.Содержание книги
Поиск на нашем сайте
Расстояние от точки до прямой Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как Доказательство. Пусть точка М 1(х 1, у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x 0) + B(y – y0) + Ax0 + By0 + C = 0, то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
Теорема доказана.
Уравнение прямой в отрезках Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу. Нормальное уравнение прямой Если обе части уравнения Ах + Ву + С = 0 разделить на число
xcosφ + ysinφ - p = 0 – нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ? С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох. C ледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
17. Эллипс. Каноническое уравнение эллипса. Геометрические свойства и построение эллипса. Специальные термины. Э́ллипс — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F 1 и F 2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть | F 1 M | + | F 2 M | = 2 a, причем | F 1 F 2 | < 2 a. Каноническое уравнение Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Построение: 1)С помощью циркуля 2) Два фокуса и натянутая нитка
3) Эллипсограф (Эллипсограф состоит из двух ползунов, которые могут двигаться по двум перпендикулярным канавкам или направляющим. Ползуны прикреплены к стержню посредством шарниров, и находятся на фиксированном расстоянии друг от друга вдоль стержня. Ползуны движутся вперёд и назад — каждый по своей канавке, — и конец стержня описывает эллипс на плоскости. Полуоси эллипса a и b представляют собой расстояния от конца стержня до шарниров на ползунах. Обычно расстояния a и b можно варьировать, и тем самым менять форму и размеры описываемого эллипса) (Свойства эллипса.) 1. В канонической для эллипса системе координат, все точки эллипса находятся в прямоугольнике
2. Точки эллипсе. 3. Эллипс является кривой, симметричной относительно своих главных осей. 4. Центр эллипса является его центром симметрии.
§ § § §
Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
18. Гипербола. Канонические уравнения гипербол. Геометрические свойства и построение гиперболы. Специальные термины Гипе́рбола (др.-греч. ὑπερβολή, от др.-греч. βαλειν — «бросать», ὑπερ — «сверх») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F 1 и F 2 (называемых фокусами) постоянно. Точнее,
Соотношения Для характеристик гиперболы определённых выше подчиняются следующим соотношениям
Канонический вид Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду
Связанные определения Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F 1 и F 2.Директрисы гиперболы обозначены линиями двойной толщины и обозначены D 1 и D 2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зеленым). Вершины гиперболы обозначены как ± a. Параметры гиперболы обозначают следующее:
a — расстояние от центра C до каждой из вершин Свойства § Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная. § Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы. § Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой. 19. Парабола. Каноническое уравнение параболы. Геометрические свойства и построение параболы. Специальные термины. Пара́бола — геометрическое место точек, равноудалённых от данной прямой (называемойдиректрисой параболы) и данной точки (называемой фокусом параболы). Каноническое уравнение параболы в прямоугольной системе координат:
Свойства § 1Парабола — кривая второго порядка. § 2Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе. § 3Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. § 4Для параболы Для параболы § 5Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе. § 6Парабола является антиподерой прямой. § Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб. § 7При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
20. Нормальный вектор плоскости. Уравнение плоскости проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости, частный случай общего уравнения плоскости. Векторное уравнение плоскости. Взаимное расположение двух плоскостей. Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости по точке и нормальному вектору
В координатах
Частные случаи общего уравнения плоскости: 1) By + Cz + D = 0 - параллельна оси Ox; 2) Ax + Cz + D = 0 - параллельна оси Oy; 3) Ax + By + D = 0 - параллельна оси Oz; 4) Cz + D = 0 - параллельна оси Oxy; 5) By + D = 0 - параллельна оси Oxz;
6) Ax + D = 0 - параллельна оси Oyz; 7) Ax + By + Cz = 0 - проходит через начало координат; 8) By + Cz = 0 - проходит через ось Ox; 9) Ax + Cz = 0 - проходит через ось Oy; 10) Ax + By = 0 - проходит через ось Oz; 11) z = 0 - плоскость Oxy; 12) y = 0 - плоскость Oxz; 13) x = 0 - плоскость Oyz. Общее уравнение плоскости:
Ах + Ву + Сz + D = 0, где А, B и C не равны нулю одновременно. Коэффициенты А, B и C являются координатами нормального вектора плоскости (т.е. вектора, перпендикулярного плоскости). При А
где a = – D / A, b = – D / B, c = – D / C. Эта плоскость проходит через точки (a, 0, 0), (0, b, 0) и (0, 0, с), т.е. отсекает на осях координат отрезки длиной a, b и c.
Уравнение плоскости, проходящей через точку (х 0 , у 0, z 0 ) и перпендикулярной вектору (А, В, C):
А (х – х 0) + В (у – у 0) + С (z – z 0) = 0. Условие параллельности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
AF – BE = BG – CF = AG – CE = 0.
Условие перпендикулярности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
АE+ ВF+ СG = 0.
Расстояние между двумя точками (х 1 , у 1, z 1 ) и(x 2, y 2, z 2):
Расстояние от точки (х 0 , у 0, z 0 ) до плоскости Ах + Ву + Сz + D = 0:
Угол
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.246.20 (0.01 с.) |

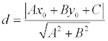 .
. (1)
(1)

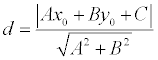
 или
или 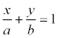 , где
, где 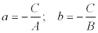
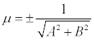 , которое называется нормирующем множителем, то получим
, которое называется нормирующем множителем, то получим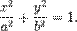
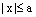 ,
,  .
. лежат на
лежат на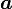 — большая полуось;
— большая полуось; — малая полуось;
— малая полуось;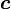 — фокальный радиус (полурасстояние между фокусами);
— фокальный радиус (полурасстояние между фокусами); — фокальный параметр;
— фокальный параметр;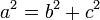 уравнение соотношения между осями и фокусом
уравнение соотношения между осями и фокусом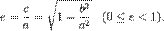 эксцентриситет
эксцентриситет фокальный параметр
фокальный параметр каноническое уравнение
каноническое уравнение причем | F 1 F 2 | > 2 a > 0.
причем | F 1 F 2 | > 2 a > 0.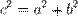 .
. .
. .
. .
. .
. .
. .
. .
.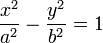 ,где большая a и малая b полуоси.
,где большая a и малая b полуоси.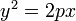 (или
(или  , если поменять местами оси).
, если поменять местами оси).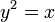 фокус находится в точке (0,25; 0).
фокус находится в точке (0,25; 0).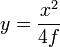 фокус находится в точке (0; f).
фокус находится в точке (0; f).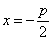 директриса параболы
директриса параболы фокальный радиус
фокальный радиус
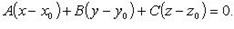

 0, В
0, В 
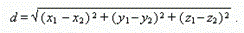
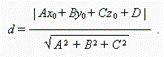
 между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:



