
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейное (векторное) пространство. Линейная зависимость и независимость векторов. Базис и размерность векторного пространства. Евклидово пространство. Неравенство коши-буняковскогоСодержание книги
Поиск на нашем сайте
Определение линейного пространства Пусть V - непустое множество (его элементы будем называть векторами и обозначать X,Y,Z, в котором установлены правила: 1) любым двум элементам X,Y c V соответствует третий элемент X+y c V называемый суммой элементов X,Y (внутренняя операция); 2) каждому X c V и каждому a c R отвечает определенный элемент aX (внешняя операция). Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы: I. II. III. IV. V. VI. VII. VIII.
Линейная зависимость и независимость векторов Система Система
Размерность линейного пространства Линейное пространство V называется n -мерным (имеет размерность n), если в нем: 1) существует n линейно независимых векторов; 2) любая система n + 1 векторов линейно зависима. Обозначения: n = dim V; Базис - любая упорядоченная система e1,e2…en из n линейно независимых векторов пространства Vn. Евкли́дово простра́нство (также Эвкли́дово простра́нство) — n-мерное векторное пространство, в котором определено скалярное произведение. Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы. Пусть дано линейное пространство L со скалярным произведением
причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).
14. Уравнение линий на плоскости(декартовые, параметрические). направляющий вектор прямой на плоскости. параметрические векторные и канонические уравнения прямой на плоскости. Уравнение прямой проходящей через две данные точки. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. Уравнение прямой по точке и вектору нормали Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0.
Уравнение прямой, проходящей через две точки Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
Уравнение прямой по точке и угловому коэффициенту Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
Уравнение прямой по точке и направляющему вектору Определение. Каждый ненулевой вектор Ах + Ву + С = 0. Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1= 0 параллельны, когда пропорциональны коэффициенты А1= λА, В1= λВ. Если еще и С1= λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой Определение. Прямая, проходящая через точку М1 (х1, у1) и перпендикулярная к прямой у = kx + b представляется уравнением:
Параметрические уравнения прямой Параметрические уравнения прямой могут быть записаны в виде:
где t — производный параметр, ax, ay — координаты x и y направляющего вектора прямой, при этом
Смысл параметра t аналогичен параметру в векторно-параметрическом уравнении. Каноническое уравнение прямой Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое: Вывод
где Нормальный вектор прямой на плоскости. Уравнение прямой, проходящей через данную точку перпендикулярную данному вектору. Общее уравнение прямой. Уравнения прямой с угловым коэффициентом. Взаимное расположение двух прямых на плоскости Нормальным вектором прямой называется любой ненулевой вектор, перпендикулярный этой прямой.
Ах + Ву + С = 0 - общее уравнение прямой. Уравнение прямой вида y=kx+b
называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой. Теорема. В уравнении прямой с угловым коэффициентом y=kx+b
угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:
Взаимное расположение: Пусть – общие уравнения двух прямых на координатной плоскости Оху. Тогда 1) если 2) если 3) если Доказательство. Условие
Если же
Если же прямые не совпадают и не пересекаются, то остается случай
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.166.224 (0.007 с.) |



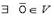 (нулевой элемент, такой, что
(нулевой элемент, такой, что 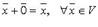 ).
).




 линейно зависима что
линейно зависима что 
 линейно независима
линейно независима 
 .
. . Пусть
. Пусть  — норма, порождённая скалярным произведением, то есть
— норма, порождённая скалярным произведением, то есть  . Тогда для любых
. Тогда для любых  имеем:
имеем:


 (α1, α2), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой
(α1, α2), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой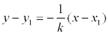
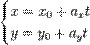



 — координаты
— координаты  и
и  направляющего вектора прямой,
направляющего вектора прямой,  и
и 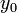 координаты точки, принадлежащей прямой.
координаты точки, принадлежащей прямой.
 .
. и
и 
 , то прямые
, то прямые  и
и 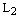 совпадают;
совпадают; , то прямые
, то прямые  , то прямые пересекаются.
, то прямые пересекаются. равносильно коллинеарности нормальных векторов данных прямых:
равносильно коллинеарности нормальных векторов данных прямых: . Поэтому, если
. Поэтому, если  и прямые пересекаются.
и прямые пересекаются.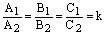 , то
, то 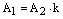 ,
,  ,
,  и уравнение прямой
и уравнение прямой  или
или  , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности
, т.е. прямые совпадают. Заметим, что коэффициент пропорциональности  , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.
, иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.


