Прямокутні проекції прямої загального положення

На рис. 2.11 показано відрізок АВ прямої d, розташованої похило до всіх площин проекцій, така пряма називається прямою загального положення.

Рис. 2.11 Рис. 2.12

Побудова епюра прямої

1. Будують проекції точок, через які проходить пряма d.

2. Однойменні проекції точок з’єднують.

3. Відрізок АВ прямої d визначений своїми проекціями. Проекції такого відрізка розташовані похило до осей проекцій (рис.2.12). Якщо кут, який утворює пряма з площиною П₁, позначати через α (рис.2.11, 2.12), з площиною П₂ – через β, а з площиною П₃ – через γ, то:

A₁B₁ = AB * cos α;

A₂B₂ = AB * cos β;

A₃B₃ = AB * cos γ.

Отже, кожна проекція відрізка прямої загального положення менша за цей відрізок.

Пряму на ортогональному рисунку можна визначити не тільки проекціями відрізка, але й проекціями деякої довільної частини її, не вказуючи кінцевих точок цієї частини. У такому разі позначають проекцію прямої тільки однією малою буквою, яка віднесена до якої-небудь точки прямої, або ж до проекції в цілому.

 

 

Сліди прямої

Пряма загального положення перетинає всі три площини проекцій. Точки перетину прямої з площинами проекцій називають слідами, або точками нульового рівня. Залежно від того, з якою площиною проекцій перетинається пряма d (рис.3.1),сліди умовно позначають і називають: Н - горизонтальний слід прямої, F – фронтальний слід прямої, Р – профільний слід прямої.

H₁, H₂, H₃, F₁, F₂, F₃, P₁, P₂, P₃ – відповідно горизонтальна, фронтальна і профільна проекції слідів H, F і Р. При цьому H₁ = H, F₂ = F, P₃ = P (рис. 2.11,2.13).

Проекції слідів будують, виходячи з умов належності цих точок прямої до площин проекцій (рис. 2.11, 2.13):

1. H₁ = H, H₂ є x₁₂,, H₃ є y₁₂;

2. F₂ = F, F₁ є x₁₂,, F₃ є z₂₃;

3. P₃ = P, P₁ є y₁, P₂ є z₂₃..

Побудова слідів прямої (рис. 2.13).

1. Горизонтальний слід H:

- будують фронтальну проекцію горизонтального сліду H₂, як результат перетину фронтальної проекції прямої d₂ з x ₁₂;

- через точку H₂ проводять вертикальну лінію зв’язку;

- будують горизонтальну проекцію горизонтального сліду H₁, як результат перетину вертикальної лінії зв’язку з горизонтальною проекцією прямої d₁;

2. Фронтальний слід F:

- будують горизонтальну проекцію фронтального сліду F₁ як результат перетину горизонтальної проекції прямої d₁ з x ₁₂;

Рис. 2.13

- через точку F₁ проводять вертикальну лінію зв’язку;

- будують фронтальну проекцію фронтального сліду F₂ як результат перетину вертикальної лінії зв’язку з фронтальною проекцією прямої d₂;

3. Профільний слід P:

- будують горизонтальну проекцію профільного сліду Р₁ як результат перетину горизонтальної проекції прямої d₁ з віссю y _1;

- будують фронтальну проекцію профільного сліду Р₂ як результат перетину фронтальної проекції прямої d₂ з віссю z₂₃.

 

Прямі особливого положення

Відносно площин проекцій пряма може займати особливе положення: паралельне площині, належить площині проекцій, перпендикулярне площині проекцій.

Прямі, які паралельні одній із площин проекцій, називають прямими рівня.

1. Горизонтальна пряма – h ││ П₁ (рис. 2.14): h₂ ││ x₁₂; h₃ ││ y₃;, А₁В₁ = АВ (горизонтальна проекція відрізка дорівнює його натуральній довжині), кути β i γ нахилу її до площин П₂ і П₃ натуральні.

2. Фронтальна пряма – f ││ П₂ (рис. 2.15): f₁ ││ x₁₂; f₃ ││ z₂₃;, C₂D₂ = CD (фронтальна проекція відрізка дорівнює його натуральній довжині), кути α i γ нахилу її до площин П₁ і П₃ натуральні.

3.

Профільна пряма – р ││ П₃ (рис. 2.16): р₁ ││ y₁; p₂ ││ z₂₃;, E₃F₃ = EF (профільна проекція відрізка дорівнює його натуральній довжині).

Рис. 2.14 Рис. 2.15 Рис. 2.16

 

Якщо прямі належать площинам проекцій, то їх називають прямими нульового рівня.

Характерною ознакою ортогонального рисунка, який зображує такі прямі, буде належність двох проекцій координатним осям.

1. Пряма а є П₁ – а₂ є x₁₂, а₃ є y₃ (рис. 2.17),

2. Пряма в є П₂ – в₁ є x₁₂, в₃ є z₂₃ (рис. 2.18),

3.

Пряма с є П₃ – с₁ є y₁, c₂ є z₂₃ (рис. 2.19).

Рис. 2.17 Рис. 2.18 Рис. 2.19

 

Прямі, які паралельні двом площинам проекцій, тобто перпендикулярні третій, називають проектуючими прямими.

1. Горизонтально проектуюча пряма – а ^ П₁ (рис. 2.20): горизональна проекція – точка а = a₁ = А₁ = В₁, а₂││а₃││z₂₃, А₂В₂ = A₃B₃ = AB.

2. Фронтально проектуюча пряма – b ^ П₂ (рис. 2.21): фронтальна проекція –точка b = b₂= C₂ = D₂, b₁ ││ y₁, b₃ ││ y_{3 ,} C₁D₁ = C₃D₃ = CD.

3. Профільно проектуюча пряма – c ^ П₃ (рис. 2.22): профільна проекція –точка с = с₃= Е₃ = F₃, c₁ ││ x₁₂,, c₂ ││ x_{12 ,} E₁F₁ = E₂F₂ = EF.

Точки, які належать проектуючим прямим, називають конкуруючими відносно площин проекцій. За допомогою конкуруючих точок визначають видимість елементів фігури в проекціях. Наприклад, точки А і В належать горизонтально-проектуючій прямій a (рис. 3.10). Горизонтальні проекції всіх точок збігаються в одну а₁ = А₁ = В₁. Точка А конкурує з точкою В відносно площини П₁. Оскільки точка А має більшу висоту в порівнянні з точкою В (z_a > z_{b ),} то вона вважається видимою для спостерігача, який дивиться на П₁ зверху в напрямку проектуючої прямої а.

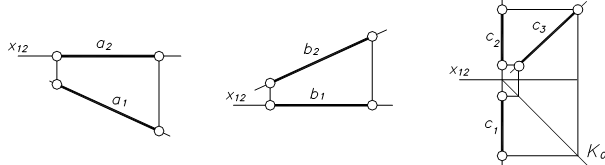
Рис. 2.20 Рис. 2.21 Рис. 2.22