
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необхідна кількість зображеньСодержание книги
Поиск на нашем сайте
Необхідна кількість зображень залежить від форми предмета, яка повинна бути зрозумілою із креслення. Іноді для цього достатньо однієї проекції як, скажімо, для предметів, які складаються із тіл обертання, для інших - дві та більше. Якщо предмет має знизу виступи або виймання некруглої форми, необхідно дати вид знизу або, в простіших випадках, показати відповідні лінії невидимого контуру на виді зверху.
Практичне Завдання За наочним зображенням деталі побудувати її горизонтальну, фронтальну та профільну проекції, виконати необхідні розрізи. Креслення виконуються на аркуші формату А3. Приклад виконання завдання наведений у додатку 1. Варіанти завдань взяти на рис. 3.12
Запитання і завдання 1. Що називають виглядом? Які є основні вигляди? 2. Як розміщують та позначають основні вигляди? 3. Які вигляди називають додатковими? Як їх розміщують та позначають? 4. Чим відрізняються місцеві вигляди від додаткових? 5. У чому відмінність між розрізом і перерізом? 6. Як поділяють розрізи залежно від кількості січних площин? 7. Як виконують місцевий розріз? 8. У яких випадках прості розрізи не позначаються? 9. Як оформити поєднання частини вигляду з частиною розрізу? 10. Чим відрізняється накладений переріз від винесеного? Коли переріз не позначається? 11. Як виконують кілька однакових перерізів, що належать одному предмету? 12. Що називають виносним елементом і як його виконують? 13. Яка умовність дозволяється при зображенні симетричних зображень? 14. Як зображують кілька однакових рівномірно розміщених елементів? 15. Як показують у розрізі болти, гвинти, шпильки, вали, шатуни тощо? 16. Як зображують на розрізі тонкі стінки та ребра жорсткості?
Варіанти завдань (проекційне креслення)
Вар. 3 Вар. 4
Рис. 3.12

Вар. 5 Вар. 6
Рис. 3.12 (продовження)
Вар. 11 Вар. 12
Рис. 3.12 (продовження)
Вар. 13 Вар. 14

Вар. 15 Вар. 16
Рис. 3.12 (продовження)
 Вар. 17 Вар. 18 Вар. 17 Вар. 18
Вар. 19 Вар. 20
Рис. 3.12 (продовження)
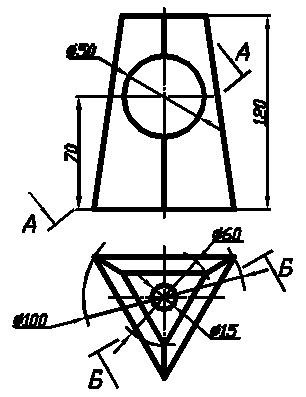
Вар. 21 Вар. 22
Вар. 23 Вар. 24
Рис. 3.12 (продовження)
Вар. 25 Вар. 26
Вар. 27 Вар. 28
Рис. 3.12 (продовження)
Вар. 29 Вар. 30
Рис. 3.12 (закінчення)
АКСОНОМЕТРИЧНІ ПРОЕКЦІЇ
Основні поняття та визначення Розглянуті прямокутні проекції знаходять широке застосування в техниці при побудові креслень. Це пояснюється простотою виконання креслень за допомогою прямокутного проектування. За допомогою креслень, побудованих у прямокутних проекціях, якщо ії доповнити допоміжними видами, розрізами і перерізами, можна одержати уяву про форму зображеного предмета. Але такі зображення недостатньо наочні. Тому в деяких випадках виникає потреба, поруч з кресленням геометричної фігури, яке виконане в прямокутних проекціях, мати її наочне зображення, що складається тільки з однієї проекції. Таке зображення можна одержати за допомогою проектування оригіналу на одну площину, яка зветься картинною площиною. Щоб таке креслення зробити оберненим, його доповнюють проекцією декартової системи координат, до якої попередньо була віднесена зображувана фігура. Такий спосіб одержання креслення називають аксонометричним, а одержане за його допомогою однопроекційне зображення геометричної фігури аксонометричною проекцією. Отже, аксонометричними проекціями називають зображення, які одержані шляхом проектування паралельними променями предмета разом з осями прямокутних координат, до яких належить предмет, на одну площину аксонометричних проекцій.
Утворення і види аксонометричних проекцій. Рис. 4.1
Утворення аксонометричних проекцій розглянемо на прикладі побудови аксонометричної проекції піраміди SA1O1C1 , яка належить до декартової системи координат Оxyz (рис. 4.1). При паралельному проектуванні за напрямком s на площині картини П¢ одержимо аксонометричну проекцію S¢A¢1O¢1C¢1 даної піраміди й аксонометричну проекцію О¢x¢y¢z¢ декартової системи координат. Припустимо, що у піраміди О1S=O1A1=O1C1 і, окрім того ці ребра є частинами координатних осей. Основа пірамади лежить у горизонтальній площині координатної системи, тому вона збігається і з самою проекцією на цю площину. Аксонометрична проекція O¢1A¢1C¢1 горизонтальної проекції основи (первинної проекції) називається вторинною проекцією основи. Отже, на аксонометричному кресленні вторинна й аксонометрична проекція предмета забезпечують метричну визначеність і оберненісь однокартинного зображення. В аксонометричних проекціях зберігаються всі властивості паралельних проекцій. На практиці вимірювання вздовж аксонометричних осей виконують в однакових одиницях – міліметрах, тому одиничні натуральні масштабні відрізки (О1S, О1А, О1С) та їх аксонометрію на кресленні не показують. Коефіцієнти спотворення за осями в аксонометрії визначають відношенням аксонометричних координатних відрізків до їх натуральної довжини при однакових одиницях виміру:
При побудові аксонометричних проекцій проектуючі промені можуть бути спрямовані перпендикулярно або під кутом φ≠90º до площини аксонометричних проекцій. Аксонометричні проекції, які одержують у першому випадку, називають прямокутним и, в другому – косокутними. Залежно від порівнювальної величини коефіцієнтів спотворення за осями розрізнюють три види аксонометричних проекцій; - ізометрія – всі три коефіцієнти спотворення рівні між собою U=V=W; - диметрія – два коефіцієнти спотворення рівні між собою і відрізняються від третьго U=W≠V; - триметрія – всі три коефіцієнти спотворення не рівні між собою U≠V≠W. Коефіцієнти спотворення зв¢язані таким співвідношенням:
ГОСТ 2.317-69 передбачає використання в інженерній практиці двох прямокутних аксонометрій: прямокутної аксонометрії та прямокутної диметрії.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.92 (0.006 с.) |



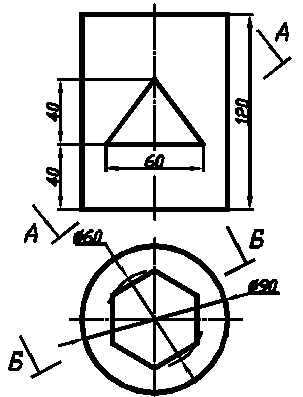 Вар. 1 Вар. 2
Вар. 1 Вар. 2


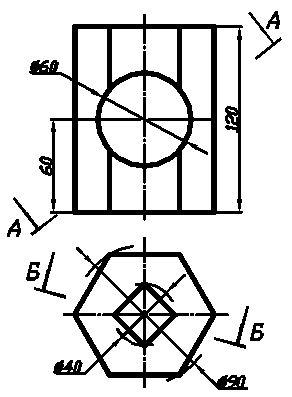 Вар. 7 Вар. 8
Вар. 7 Вар. 8

 Вар. 9 Вар. 10
Вар. 9 Вар. 10
















 - по осі Оx;
- по осі Оx;  - по осі Оy;
- по осі Оy;  - по осі Оz.
- по осі Оz.



