
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
І. А. Малякова, Д. Ю. Калина, Л. В. КорольоваСодержание книги
Поиск на нашем сайте
І.А. МАЛЯКОВА, Д.Ю. КАЛИНА, Л.В. КОРОЛЬОВА ІНЖЕНЕРНА ТА КОМП’ЮТЕРНА ГРАФІКА Частина І
НАВЧАЛЬНИЙ ПОСІБНИК
для підготовки фахівців за напрямами “екологія”, “геодезія, картографія та землевпорядкування”, “електронні апарати”, “ком`ютеризовані системи, автоматика і управління”, “комп`ютерна інженерія”, “електромеханіка”
Кременчук 2003 І.А. Малякова, Д.Ю. Калина, Л.В. Корольова. - Інженерна та комп’ютерна графіка. Частина І: Навчальний посібник для підготовки фахівців за напрямами “екологія”, “геодезія, картографія та землевпорядкування”, “електронні апарати”, “ком`ютеризовані системи, автоматика і управління”, “комп`ютерна інженерія”, “електромеханіка”. – Кременчук: КДПУ, 2003. – 144 с.
Затверджено методичною радою університету Протокол №______від_____________________ Голова методичної ради___________________проф. В.В. Костін
Кременчук 2003
ВСТУП Навчальний посібник призначений для підготовки фахівців за напрямами “екологія”, “геодезія, картографія та землевпорядкування”, “електронні апарати”, “ком`ютеризовані системи, автоматика і управління”, “комп`ютерна інженерія”, “електромеханіка”. У ньому розглядається перший розділ предмета “Нарисна геометрія” та теми “Геометричне креслення”, “Проекційне креслення”, “Зображення та позначення різьбових деталей і з’єднань”, “Ескізування”, “Виконання робочого креслення деталі”, “Виконання складального креслення”. Загальність і різноманіття дисципліни “Інженерна графіка”, з однієї сторони, та необхідність її викладання в обмеженому об’ємі навчального часу, з другої сторони, створили необхідність певного підходу до структури цього навчального посібника. У ньому викладені теоретичні довідки, подані методичні рекомендації щодо виконання графічних робіт, питання для самоперевірки, а також наведені приклади виконання графічних завданнь. Матеріалу, який наведено в навчальному посібнику, достатньо, щоб розвинути просторове уявлення студентів, допомогти розібратися в тих чи інших поняттях даної дисципліни, закріпити знання з усіх розділів курсу, отримати навички в оформленні конструкторської документації згідно зі стандартами ЕСКД. Студенти виконують дві контрольні роботи за темами “Нарисна геометрія” та “Інженерна графіка”. Розділ “Комп`ютерна графіка” розглядається у частині ІІ.
Лінії креслення ГОСТ 2.303-68 визначає найменування ліній, які використовуються для креслення, їх нарис, основне значення й товщину. Згідно з цим стандартом використовуються лінії трьох типів: суцільні, штрихові та штрих-пунктирні (рис. 1.2).
Рис 1.2 Суцільні лініїподіляються на основні, тонкі, хвилясті й хвилясті зі зламами. Суцільну товсту основну лінію використовують для видимого контуру, видимих ліній переходу, контуру перерізів, які входять до складу розрізів. Товщину S цієї лінії беруть у діапазоні 0,5...1,1 мм, залежно від розміру й складності зображення і формату креслення. Суцільні тонкі лінії використовуються як розмірні й виносні, лінії штриховки розрізів та перерізів, лінії–виноски, осі проекцій, лінії контуру накладених перерізів, лінії побудов тощо. Суцільну хвилясту лінію використовують для зображення обривів та розмежування виду і розрізу. Суцільна тонка лінія зі зламами використовується для викреслення довгих ліній обриву. Штрихові лінії поділяються на штрихові й розімкнені. Штрихові лінії використовують для зображення невидимого контуру й невидимих ліній переходу. Розімкнена лінія використовується для позначення ліній перерізу, тобто січної площини, у розрізах і перерізах. Штрихпунктирні лінії поділяються на тонкі, потовщені й тонкі з двома крапками. Штрихпунктирна тонка лінія використовується для зображення центрових та осьових ліній, які є осями симетрії накладених або винесених перерізів. Штрихпунктирна потовщена лінія використовується для позначення поверхонь, які підлягають термообробці або покриттю. Штрихпунктирна тонка лінія з двома крапками має такий самий нарис, як і штрихпунктирна, але має дві крапки в інтервалі між штрихами. Використовується для зображення граничних деталей, частин виробу в крайніх або проміжних положеннях, розгортки, яка сполучена з видом, ліній згину на розгортках.
Виконання штриховки Графічне зображення матеріалів у перерізах наноситься за допомогою штриховки (ГОСТ 2.306-68). Штриховку виконують суцільними тонкими лініями під кутом 45º або до лінії контуру зображення, або до його осі, або до ліній рамки креслення. Якщо лінії штриховки, проведені під кутом 45º до ліній рамки креслення, є паралельними лініями контуру або основним лініям, потрібно замість 45º вибрати кут 30º або 60º. Лінії штриховки можна наносити з нахилом як у правий, так і в лівий бік, але в один і той самий бік на всіх перерізах однієї деталі. Частота нанесення ліній штриховки повинна бути однаковою для всіх перерізів даної деталі та дорівнювати 1-10 мм. Вузькі та довгі площі перерізів (товщиною на кресленні від 2 до 4 мм) потрібно штрихувати повністю тільки на кінцях та біля контурів отворів, іншу площу перерізу – невеликими ділянками в декількох місцях.
Нанесення розмірів на кресленні Правила нанесення розмірів установлюються ГОСТом 2.307-68. Для виконання графічної роботи № 1 потрібно знати наступне: - розміри на кресленнях указують виносними лініями, розмірними лініями і розмірними числами; - розмірну лінію з обох кінців обмежують стрілками (крім розмірної лінії радіуса); - виносні лінії повинні виходити за кінці стрілок розмірної лінії на 1-5 мм; - розмірні та виносні лінії виконують суцільними тонкими лініями; - за можливостю розмірні лінії потрібно наносити поза контуром зображення; - відстань між паралельними розмірними лініями повинна бути не менше
Нахил прямої ВС відносно АВ показаний на рис. 1.2. Перед розмірним числом, яке визначає нахил, наносять знак нахилу, гострий кут якого направлений у бік нахилу. Знак і величину нахилу вказують на полочці лінії - виноски, яка закінчується стрілкою. Нахил може бути заданий відношенням значень h і l (наприклад, при h=1, l=10, відношення – 1:10), десятковим дробом (0,1), у процентах (10%), значенням кута нахилу. Конусність - це відношення різниці діаметрів основ конуса до відстані між ними (рис. 1.4). Перед розмірним числом, що характеризує конусність, наносять знак конусності, вершина якого спрямована в сторону вершини конуса. Конусність може бути задана відношенням значень (D-d):l (наприклад, 1:5), десятковим дробом (0,2), у процентах (70%), значенням кута. Графічне зображення конусності показане на рис. 1.4.
Побудова спряжень Побудова спряжень між двома лініями, від прямої лінії до кола і від одної дуги до другої за допомогою деякої дуги включає три елементи побудови: центр дуги спряження, точку спряження, радіус дуги спряження. Задається один з цих елементів (наприклад, радіус), інші елементи одержують побудовою. На рис. 1.5 заданий радіус спряження R, знайдені центр О2 дуги і точки А1 і А2 спряження. Для цього паралельно заданій прямій проведена пряма на відстані R і дуга, радіус якої R+R2. Шуканий центр О2 дуги R знаходиться в точці перетину прямої з проведеною дугою. Точки спряження знаходяться на перетині перпендикуляра, проведеного з центру на пряму, і на лінії, яка з’єднує центри кола і дуги спряження.
Рис. 1.5 Рис. 1.6
У прикладі на рисунку 1.6 відомий радіус R спряження двох дуг, знайдені центр О і точки А1 і А2 спряження. Шуканий центр дуги спряження знаходиться в перетині дуг, радіуси яких дорівнюють R плюс радіуси R1 і R2 кіл, які спрягаються.
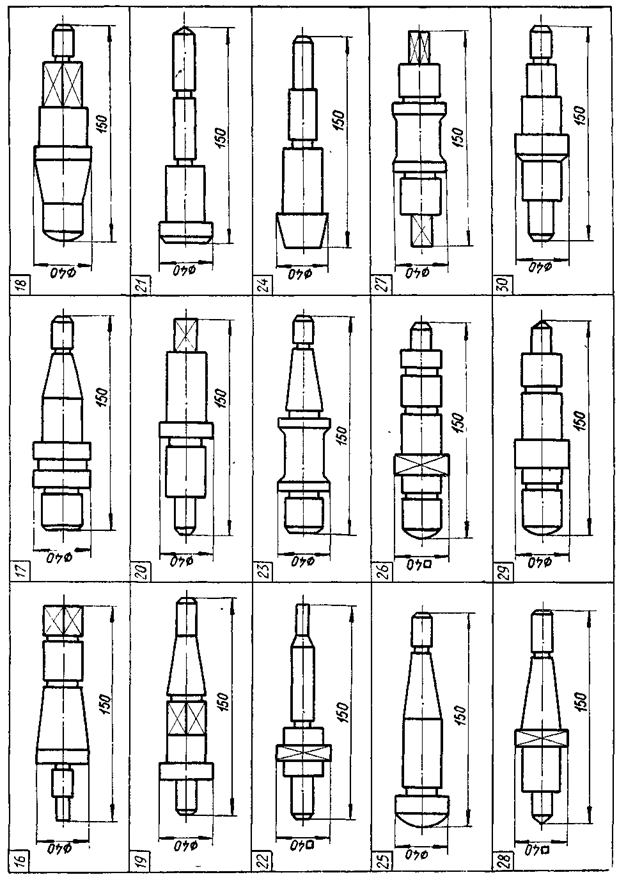
Практичне завдання На аркуші формату А3 виконати креслення перерізу профілю проката, деталі типу “Вал” та “Плоский контур”. Приклад виконання аркуша дивись у додатку 1. Варіанти завдань до аркуша 1 взяти з таблиць 1 – 2, та рис. 1.7, 1.8. Запитання і завдання 1. Що називають форматом? Чим відрізняється основний формат від додаткового? 2. Як проводять рамку креслення? 3. Де розміщують основний напис та графу 26? Які їхні розміри? 4. Назвати основні типи ліній, які застосовують під час виконання креслень, а також співвідношення їхніх товщин. 5. У яких межах можна вибирати довжину штрихів для штрихової та штрихпунктирної ліній? 6. Що таке масштаб зображення? Які масштаби рекомендує ГОСТ 2.302-68? 7. Які розміри та типи шрифтів застосовують у машинобудівному кресленні? 8. Які загальні правила виконання штриховки на кресленнях? 9. Як виконують штриховку двох суміжних деталей? 10. Як проводять розмірні та виносні лінії для прямолінійного відрізка? кола? дуги? кута? 11. На якій мінімальній відстані проводять розмірну лінію від контуру? Від паралельної розмірної лінії? 12. Як записують розмірні числа при різних нахилах розмірних ліній для 13. Як виконують розмірні лінії та наносять розмірні числа, якщо не вистачає місця для стрілок та чисел? 14. Які правила нанесення розмірів конусності та нахилу? 15. Що називають спряженням? Які його основні елементи? Рис. 1.7 (закінчення)
Рис. 1.8
Рис. 1.8 (закінчення)
Методи і види проекцій
Методи проекцій
Рис. 2.1
Зображення предмета полягає в проектуванні точок, які визначають його форму.
Види проекцій
Залежно від способу проведення проектуючих прямих проекції поділяються на центральні та паралельні. Рис. 2.2 Рис. 2.3
Якщо проектуючі прямі проходять через одну точку S, яка називається центром (полюсом) проекцій, то проектування називається центральним, полярним, або конічним (рис. 2.2). Проекціями точок А та М будуть Аі та Мі Площина AіSMі називається проектуючою площиною. Проекція Nі точки N буде віддаленою у нескінченність, оскільки проектуюча пряма SN паралельна Пі. Якщо точка, яку проектують, збігається з центром проекцій, проектуюча пряма стає невизначеною. Невизначеною буде і проекція такої точки. Центральні проекції застосовують при побудові перспективних проекцій. Фотографія якого-небудь об’єкта є також центральною проекцією. Об’єктив фотографічного апарата – центр проекцій, плівка – площина проекцій. Якщо центр проекцій S (рис. 2.2) віддалити у нескінченність, то проектуючі прямі стануть взаємно паралельними (рис. 2.3). Проектуючі прямі AAi, BBi проводять паралельно заданому напрямку проектування S, а тому вони утворюють з площиною проекцій гострий або прямий кут α. Якщо проектуючі прямі утворюють з площиною проекцій гострий кут, то проекції називають косокутними, а якщо прямий - прямокутним.
Оборотність креслення Креслення, за яким можна відтворити форму і розміри зображеного предмета, називають оборотним, воно рівнозначне оригіналу. В техніці має практичне значення тільки оборотне креслення.
Щоб зображення стало визначеним, його доповнюють додатковими даними. У практиці знайшли місце такі способи доповнення однопроекційного зображення: проекції з числовими позначками, спосіб академіка С.С. Федорова, ортогональні аксонометричніпроекції, ортогональне Спосіб побудови ортогональних креслень, систематизований і викладений французьким ученим Монжем, є основним при виконанні технічних креслень. Його вивчає нарисна геометрія.
2. 2 Точка Точка – основне невизначене поняття геометрії. Іншими якимось більш елементарними поняттями визначити її неможливо, оскільки розмірів вона не має, а тому і фігур, простіших за неї, немає. На кресленні ми зображаємо точку умовно – у вигляді якоїсь площини, перетину двох ліній або кружком.
Пряма
Визначником прямої лінії в просторі є дві точки, що не збігаються, точка і напрям, дві площини, що перерізуються. Рис. 2.11 Рис. 2.12 Побудова епюра прямої 1. Будують проекції точок, через які проходить пряма d. 2. Однойменні проекції точок з’єднують. 3. Відрізок АВ прямої d визначений своїми проекціями. Проекції такого відрізка розташовані похило до осей проекцій (рис.2.12). Якщо кут, який утворює пряма з площиною П1, позначати через α (рис.2.11, 2.12), з площиною П2 – через β, а з площиною П3 – через γ, то: A1B1 = AB * cos α; A2B2 = AB * cos β; A3B3 = AB * cos γ. Отже, кожна проекція відрізка прямої загального положення менша за цей відрізок. Пряму на ортогональному рисунку можна визначити не тільки проекціями відрізка, але й проекціями деякої довільної частини її, не вказуючи кінцевих точок цієї частини. У такому разі позначають проекцію прямої тільки однією малою буквою, яка віднесена до якої-небудь точки прямої, або ж до проекції в цілому.
Сліди прямої Пряма загального положення перетинає всі три площини проекцій. Точки перетину прямої з площинами проекцій називають слідами, або точками нульового рівня. Залежно від того, з якою площиною проекцій перетинається пряма d (рис.3.1),сліди умовно позначають і називають: Н - горизонтальний слід прямої, F – фронтальний слід прямої, Р – профільний слід прямої. H1, H2, H3, F1, F2, F3, P1, P2, P3 – відповідно горизонтальна, фронтальна і профільна проекції слідів H, F і Р. При цьому H1 = H, F2 = F, P3 = P (рис. 2.11,2.13). Проекції слідів будують, виходячи з умов належності цих точок прямої до площин проекцій (рис. 2.11, 2.13): 1. H1 = H, H2 є x12,, H3 є y12; 2. F2 = F, F1 є x12,, F3 є z23; 3. P3 = P, P1 є y1, P2 є z23.. Побудова слідів прямої (рис. 2.13).
- будують фронтальну проекцію горизонтального сліду H2, як результат перетину фронтальної проекції прямої d2 з x 12; - через точку H2 проводять вертикальну лінію зв’язку; - будують горизонтальну проекцію горизонтального сліду H1, як результат перетину вертикальної лінії зв’язку з горизонтальною проекцією прямої d1; 2. Фронтальний слід F: - будують горизонтальну проекцію фронтального сліду F1 як результат перетину горизонтальної проекції прямої d1 з x 12; Рис. 2.13 - через точку F1 проводять вертикальну лінію зв’язку; - будують фронтальну проекцію фронтального сліду F2 як результат перетину вертикальної лінії зв’язку з фронтальною проекцією прямої d2; 3. Профільний слід P: - будують горизонтальну проекцію профільного сліду Р1 як результат перетину горизонтальної проекції прямої d1 з віссю y 1; - будують фронтальну проекцію профільного сліду Р2 як результат перетину фронтальної проекції прямої d2 з віссю z23.
Прямі особливого положення Відносно площин проекцій пряма може займати особливе положення: паралельне площині, належить площині проекцій, перпендикулярне площині проекцій. Прямі, які паралельні одній із площин проекцій, називають прямими рівня. 1. Горизонтальна пряма – h ││ П1 (рис. 2.14): h2 ││ x12; h3 ││ y3;, А1В1 = АВ (горизонтальна проекція відрізка дорівнює його натуральній довжині), кути β i γ нахилу її до площин П2 і П3 натуральні. 2. Фронтальна пряма – f ││ П2 (рис. 2.15): f1 ││ x12; f3 ││ z23;, C2D2 = CD (фронтальна проекція відрізка дорівнює його натуральній довжині), кути α i γ нахилу її до площин П1 і П3 натуральні. 3.
Профільна пряма – р ││ П3 (рис. 2.16): р1 ││ y1; p2 ││ z23;, E3F3 = EF (профільна проекція відрізка дорівнює його натуральній довжині). Рис. 2.14 Рис. 2.15 Рис. 2.16
Якщо прямі належать площинам проекцій, то їх називають прямими нульового рівня. Характерною ознакою ортогонального рисунка, який зображує такі прямі, буде належність двох проекцій координатним осям. 1. Пряма а є П1 – а2 є x12, а3 є y3 (рис. 2.17), 2. Пряма в є П2 – в1 є x12, в3 є z23 (рис. 2.18), 3.
Пряма с є П3 – с1 є y1, c2 є z23 (рис. 2.19). Рис. 2.17 Рис. 2.18 Рис. 2.19
Прямі, які паралельні двом площинам проекцій, тобто перпендикулярні третій, називають проектуючими прямими. 1. Горизонтально проектуюча пряма – а ^ П1 (рис. 2.20): горизональна проекція – точка а = a1 = А1 = В1, а2││а3││z23, А2В2 = A3B3 = AB. 2. Фронтально проектуюча пряма – b ^ П2 (рис. 2.21): фронтальна проекція –точка b = b2= C2 = D2, b1 ││ y1, b3 ││ y3 , C1D1 = C3D3 = CD. 3. Профільно проектуюча пряма – c ^ П3 (рис. 2.22): профільна проекція –точка с = с3= Е3 = F3, c1 ││ x12,, c2 ││ x12 , E1F1 = E2F2 = EF. Точки, які належать проектуючим прямим, називають конкуруючими відносно площин проекцій. За допомогою конкуруючих точок визначають видимість елементів фігури в проекціях. Наприклад, точки А і В належать горизонтально-проектуючій прямій a (рис. 3.10). Горизонтальні проекції всіх точок збігаються в одну а1 = А1 = В1. Точка А конкурує з точкою В відносно площини П1. Оскільки точка А має більшу висоту в порівнянні з точкою В (za > zb ), то вона вважається видимою для спостерігача, який дивиться на П1 зверху в напрямку проектуючої прямої а.
Рис. 2.23 Рис. 2.24 ПЛОЩИНА
Рис. 2.35
Рис. 2.36
Властивості проектуючих площин: 1. Проекція точки, а також будь-якої геометричної фігури, яка лежить у проектуючій площині, належить (рис. 2.34), фронтальному (рис. 2.35), або профільному (рис. 2.36) сліду – проекції цієї площини. 2. Сліди-проекції утворюють з осями проекцій кути a, b, g, які дорівнюють дійсним кутам нахилу площини до площин проекцій. 3. Другий слід f20 (рис.45), h10 (рис.46), p30 (рис.47) завжди перпендикулярний до осі проекцій. До площин рівня належать: горизонтальні (θ // П1), фронтальні (Ф // П2) і профільні (∆ // П3). Ці площини перпендикулярні двом іншим площинам проекцій. На рис. 2.37 і 2.38 зображені відповідно горизонтальна і фронтальна площини рівня. Площинам рівня притаманні перша і друга властивості проектуючих площин. Крім того, прямі лінії і фігури, що є підмножиною цих площин, проектуються в дійсну величину на однойменну площину проекцій, а сліди – проекції завжди перпендикулярні осям проекцій.
Рис. 2.37 Рис. 2.38
Пряма і точка в площині Точка належить площині, якщо вона лежить на прямій, що належить цій площині. Точка А (рис. 2.39) лежить на прямій в (на проекційному рисунку її проекції А1 і А2 знаходяться на вертикальній лінії проекційного зв׳язку на однойменних проекціях в1 і в2 прямої в). Отже, точка А лежить у площині ∆ (а ∩в). За такою самою ознакою точка В
Пряма належить площині, якщо має з нею дві спільні точки.. Пряма п проходить через точки А і в, що належать площині ∆ (на проекційному рисунку А1  в, А2 в, А2  в2 , в1 в2 , в1  а1, в2 а1, в2  а2). Отже, пряма п має дві спільні точки з площиною і належить площині ∆ (а ∩ в). а2). Отже, пряма п має дві спільні точки з площиною і належить площині ∆ (а ∩ в).
Рис. 2.39 Рис. 2.40 Пряма належить площині в тому і в тому випадку, коли має одну спільну точку з площиною і паралельна іншій прямій, яка належить цій площині. На рис. 2.40 подано площину Q (ABF). Пряма l проходить через точку С, що лежить на стороні [ AF ] (на рисунку С1
Основні лінії площини До основних ліній площини належать: 1. Прямі, які лежать у площині та паралельні одній з площин проекцій. 2. Прямі, які лежать у площині та перпендикулярні до будь-якої лінії, згаданої у першому пункті. Прямі, що паралельні площині проекцій, належать площині рівня, тому їх називають прямими (лініями) рівня. 1. h || h0 2. f || f0 3. p || p0 Сліди h0, f0, p0 площини R також належать до основних ліній. Їх називають нульовими лініями рівня. Пряма, яка знаходиться в площині та перпендикулярна до горизонталі (фронталі або профільної прямої) називається лінією найбільшого нахилу до площини проекцій П1 (П2 або П3). Ці лінії визначають кути нахилу площини до площин проекцій. 1. m ^ h - лінія найбільшого нахилу до горизонтальної площини проекцій; 2. n ^ f - лінія найбільшого нахилу до фронтальної площини проекцій; 3. l ^ p - лінія найбільшого нахилу до профільної площини проекцій. Розглянемо детальніше деякі з цих основних ліній.
Горизонтальна пряма площини (h Усі точки горизонталі мають однакові висоти, тому на ортогональному (рис. 2.41 б) фронтальна проекція h2 горизонталі h паралельна осі х12, а горизонтальна проекція h1 паралельна горизонтальному сліду площини (h1 Фронтальна пряма площини (h Усі точки фронталі мають однакові глибини, тому на ортогональному рисунку (рис. 2.42 б) горизонтальна проекція f1 фронталі f2 паралельна фронтальному сліду площини (f
Рис. 2.42 Практичне завдання 1) за заданими координатами точок А, В, С побудувати ортогональне креслення відрізка АВ та точки С; 2) визначити горизонтальний (H) і фронтальний (F) сліди прямої АВ; 3) визначити дійсну довжину відрізка АВ; 4) величину кутів a та b нахилу прямої АВ до площин проекції П1 і П2; 5) пряму n, котра проходить через точку С паралельно прямій АВ; 5) пряму горизонтального (h) та фронтального (f) рівня, яка проходить через точку С та перетинає пряму АВ. Таблиця 1
Запитання та завдання 1. Назвіть основні методи проеціювання і поясніть їх сутність. 2. Сформулюйте основні властивості паралельного проеціювання. 3. Що являє собою просторова система координат? 4. Як утворюється комплексне креслення? 5. Укажіть основні властивості креслення. 6. Які координати має точка в просторовій системі координат? 7. Побудуйте проекції точок, розташованих у різних чвертях простору. 8. Як побудувати третю проекцію точки за двома заданими? 9. Які положення може займати пряма відносно площин проекції? 10. Укажіть особливі положення прямих. 11. Що називають слідами прямої? 12. Побудуйте сліди прямих, які займають різні положення відносно площин проекції. 13. Як за даними проекціями відрізка прямої визначити його дійсну довжину? 14. Як зображуються на комплексному кресленні паралельні, мимобіжні прямі та прямі, що перетинаються? 15. Назвіть способи задання площини на епюрі. 16. Що таке сліди площини? 17. Назвіть властивості площин особливого положення. 18. Як зображуються на комплексному кресленні прямі особливого положення, які належать плошині?
Зображення та їх умовності Дві проекції визначають положення кожної точки в просторі. Для зображення найбільш простих предметів буває достатньо однієї, двох проекцій. Для зображення більш складних - необхідно три і більше проекцій. Шість основних видів стандартного розташування проекцій показані на рис.3.1. Це розгорнуті грані паралелепіпеда, всередині якого розташовують предмет, що проектують (рис. 3.1а). Пояснюючі написи (рис. 3.1б) на кресленнях не виконують. При іншому розташуванні виду його позначають (рис. 3.1в) – стрілкою показано напрямок проектування і поданий напис над відповідним зображенням А.
Рис. 3.1
Зображення на кресленні залежно від їхнього змісту поділяють на вигляд, розріз і переріз. Вигляд – зображення повернутої до спостерігача видимої частини поверхні предмета. Розріз – зображення предмета, розсіченого однією площиною (простий розріз) або декількома площинами (складний розріз). На розрізі показують те, що знаходиться в січній площині, й те, що розташоване за нею. Ближчу відсічену частину подумки відкидають. Розріз зображують на одній із проекцій, й інші проекції він не впливає. Про переріз інформація подається нижче.
Простий розріз При виконанні розрізів потрібно враховувати правила, які існують, умовності та спрощення. Вони будуть розглянуті на двох предметах, які показані на рис. 3.2 і 3.4 Зображені предмети складаються з наступних конструктивних елементів: на рис. 3.2 - пустотілий циліндричний стояк з трьома ребрами і круглим фланцем, знизу з чотирма отворами. На виді спереду бачимо проекцію твірної циліндра, відмічену стрілкою. Із чотирьох наскрізних отворів три позначені лише осьовими лініями на виді зверху; на рис. 3.4 - циліндричний стояк із глухим чотирикутним отвором та суцільними “приливками” ззовні, який розташований на прямокутному фланцю з чотирма отворами.
1. Несиметричні предмети розрізають зовсім або з обривом, позначають стрілками та буквами. 2. Якщо предмет симетричний (рис. 3.2), то на одній проекції з’єднують половину зовнішнього виду з половиною розрізу, та половину розрізу розташовують справа або знизу від осі симетрії проекції. Невидимі лінії, симетричні лініям, які виявляються розрізами, звичайно не показують. Вид відокремлюється від розрізу осьовою лінією. 3. Якщо січна площина проходить за віссю симетрії предмета, її на кресленні не позначають. В іншому випадку розташування площини показують розімкненою стовщеною лінією, яка дорівнює 1,5 товщини основної лінії, та стрілками із великими літерами російського алфавіту, які пишуть із зовнішнього боку ліній (рис. 3.3). Над відповідним зображенням подають напис із позначенням розрізу (наприклад, А-А).
Рис. 3.3 4. На розрізах наносять штриховку згідно з ГОСТом 2.306-68, яка характеризуює матеріал деталі (на даному прикладі штриховкою позначений метал). Штриховка на всіх проекціях предмета виконується в один бік (у більшості випадків під 45º до контурної або осьової лінії, яку приймають за основну на даному зображенні, або до основного напису креслення) із однаковим кроком. Тонкі стічки (ребра жорсткості), розсічені площиною вздовж, обводять контурною лінією і не штрихують (фронтальна проекція на рис. 3.2); розсічені площиною в поперек – штрихують.
Рис. 3.4 5. Для того, щоб включити до розрізу отвори на круглому фланці застосовують умовність – викачування: його центр мовби котять по центровому колу в напрямку, що вказаний стрілками (стрілку не креслять) на виді зверху – рис. 23. 6. Для виділення контурної лінії, яка співпадає з осьовою (рис.3.4), використовують лінію обриву. Якщо контурна лінія належить до виду, то вид розповсюджують вправо (рис. 3.5а). Якщо контурна лінія належить до розрізу, то розріз розповсюджують вліво – рис.3.4, 3.5б. Загальний випадок показаний на рис. 3.5в. Таким самим чином розділяють види і розріз, коли проекція не симетрична (рис.3.6) 7. Розріз, який служить для з’єднування будови предмета, наприклад форми отвору лише в окремому, обмеженому міс
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.012 с.) |



 Побудова нахилу та конусності
Побудова нахилу та конусності



 Відображення точок тримірного простору на площині досягається за допомогою методу проекцій, суть якого полягає у наступному. Через довільну точку А (оригінал) простору (рис. 2.1) проводять проектуючу пряму а (аÎА) до перетину її з площиною проекцій Пі в точці Аі, яка і є проекцією точки А.
Відображення точок тримірного простору на площині досягається за допомогою методу проекцій, суть якого полягає у наступному. Через довільну точку А (оригінал) простору (рис. 2.1) проводять проектуючу пряму а (аÎА) до перетину її з площиною проекцій Пі в точці Аі, яка і є проекцією точки А.
 Розглянемо з точки зору оборотності одержуване проекційне креслення. Знаючи проекцію Аі довільної точки А на площині проекції Пі і напрям проектування S (рис. 2.4), неможливо однозначно знайти її положення в просторі. Дійсно, будь-якій точці A’, A’’, A’’’ проектуючої прямої при заданому напрямку S проектування S відповідає одна і та сама проекція Аі. Отже, одна проекція точки не визначає її положення в просторі.
Розглянемо з точки зору оборотності одержуване проекційне креслення. Знаючи проекцію Аі довільної точки А на площині проекції Пі і напрям проектування S (рис. 2.4), неможливо однозначно знайти її положення в просторі. Дійсно, будь-якій точці A’, A’’, A’’’ проектуючої прямої при заданому напрямку S проектування S відповідає одна і та сама проекція Аі. Отже, одна проекція точки не визначає її положення в просторі. 1. Горизонтальний слід H:
1. Горизонтальний слід H:
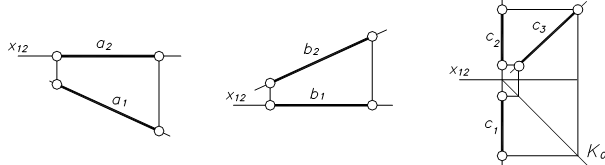
 Рис. 2.20 Рис. 2.21 Рис. 2.22
Рис. 2.20 Рис. 2.21 Рис. 2.22


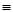 h0) або ж проходить через проекції 11 і 21 точок 1 і 2 (рис. 2.41 в) перетину з прямими m i n, які визначають площину Ф (m ∩ n).
h0) або ж проходить через проекції 11 і 21 точок 1 і 2 (рис. 2.41 в) перетину з прямими m i n, які визначають площину Ф (m ∩ n).




 Правила, умовності та спрощення, які необхідно враховувати при виконанні розрізів:
Правила, умовності та спрощення, які необхідно враховувати при виконанні розрізів:




