
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальный закон распределения случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нормальный закон распределения(закон Гаусса) играет исключительно важную роль в теории вероятностей. Во-первых, это наиболее часто встречающийся на практике закон распределения непрерывных случайных величин. Во-вторых, он являетсяпредельным законом в том смысле, что к нему при определенных условиях приближаются другие законы распределения. Нормальный закон распределения характеризуется следующей формулой для плотности вероятности:
где х – текущие значения случайной величины X; М (X) и s – ее математическое ожидание и стандартное отклонение. Из (26) видно, что если случайная величина распределена по нормальному закону, то достаточно знать только два числовых параметра: М (Х) и s, чтобы полностью знать закон ее распределения.
Величина М (Х) называется также центром рассеяния. Среднеквадратичное отклонение s характеризует ширину кривой распределения.
Естественно, что при любых значениях М (Х) и s площадь, ограниченная нормальной кривой и осью Х, остается равной 1 (условие нормировки):
Нормальное распределение симметрично, поэтому Вероятность попадания значений случайной величины Х в интервал (x 1, x 2), т.е. Р (x 1 < Х< x 2), равна: Р (x1 < Х < x2) =
Р (М (Х) – s <Х<М (Х) + s) = 0,6827 = 68,27 %. (28) Р (М (Х) – 2s <Х<М (Х)+ 2s) = 0,9545 = 95,45 %. (29) Р (М (Х) –3s <Х<М (Х) + 3s) = 0,9973 = 99,73 %. (30) Из (30) следует: практически достоверно, что значения нормально распределенной случайной величины Х с параметрами М (Х) и s лежат в интервале М (Х) ± 3s. Иначе говоря, зная М (Х) = Пример. Известно, что для здорового человека р Н крови является нормально распределенной величиной со средним значением (математическим ожиданием) 7,4 и стандартным отклонением 0,2. Определите диапазон значений этого параметра. Решение: для ответа на этот вопрос воспользуемся “правилом трех сигм”. С вероятностью равной 99,73% можно утверждать, что диапазон значений р Н для здорового человека составляет 6,8 – 8.
Глава III Элементы математической статистики 3.1. Предмет и задачи математической статистики. Генеральная и выборочная совокупность Математические законы теории вероятностей – это математическое выражение реальных закономерностей, которым подчиняются массовые случайные явления. При этом каждое исследование случайных явлений, выполняемое методами теории вероятностей, прямо или косвенно опирается на экспериментальные данные, на результаты испытаний и наблюдений. Разработка методов получения, описания и анализа экспериментальных данных, определенных в результате исследования массовых случайных явлений, составляет предмет специальной науки – математической статистики. Эти данные принято называть статистическими. Статистические данные часто можно рассматривать как совокупность экспериментальных результатов, которые представляют собой набор возможных значений случайных однородных величин (роста, массы тела, длительности пребывания больного на койке, содержания сахара в крови и т.д.). Фундаментальными понятиями математической статистики являются генеральная совокупность и выборочная совокупность (выборка). Существуют разные подходы к пониманию смысла этих величин. Мы определяем их так. Генеральная совокупность – это множество подлежащих статистическому изучению однородных объектов, которые характеризуются определенными качественными или количественными признаками. Например, конечная и реально существующая генеральная совокупность – конкретно выбранная популяция: все жители Беларуси в фиксированный момент времени или только все мужчины, или женщины, или дети. Следующий пример: бесконечная и реально существующая генеральная совокупность – множество действительных чисел, лежащих между 0 и 1. Чтобы изучить генеральную совокупность по какому-либо из ее количественных признаков Х (острота зрения, показатели анализа крови и т.д.), нужно определить закон распределения данного признака и основные характеристики этого распределения, например, математическое ожидание и дисперсию. Для этого следовало бы изучить все ее объекты и затем обработать полученный массив данных методами теории вероятностей. Однако на практике провести сплошное обследование объектов генеральной совокупности часто физически невозможно и экономически невыгодно. Поэтому обычно исследуется только часть объектов, так называемая выборка. Совокупность «n» объектов, отобранных из интересующей нас генеральной совокупности для конкретного статистического исследования, называется выборочной совокупностью или выборкой. Исследование выборки дает некоторое приближенное, оценочное значение интересующего нас параметра, принимающего различные значения для разных выборок. Таким образом, постоянная величина – значение нужной характеристики для генеральной совокупности – заменяется значением случайной величины, полученным по результатам выборки на основании некоторого правила. Поэтому главная цель выборочного метода, основного в математической статистике, – повычисленной характеристике выборки как можно точнее определить соответствующую характеристику генеральной совокупности. Это возможно лишь в том случае, когда отобранная для работы часть объектов репрезентативнацелому, т.е. типична, обладает теми же основными чертами, что и все целое. Иначе говоря, выборка должна быть представительной, т.е. по возможности полнее « представлять » свою генеральную совокупность. Это одно из важнейших требований, предъявляемых к выборке, несоблюдение которого ведет к грубым ошибкам и обесценивает результаты исследования. Например, если при изучении заболеваемости населения республики (генеральная совокупность) ишемической болезнью сердца в качестве выборки будет взята группа студентов, то результаты окажутся ошибочны, поскольку свойства выборки не будут соответствовать свойствам генеральной совокупности, как и в случае, когда в качестве выборки будут взяты только пациенты кардиологического диспансера. Репрезентативность выборки обеспечивается ее достаточным объемом и определенными правилами ее формирования, которые в данном пособии не рассматриваются. Из многочисленных задач, решаемых математической статистикой, выделим следующие. 1. Определение статистических характеристик выборки (методы описательной статистики). 2. Определение параметров генеральной совокупности по данным выборки: точечные оценки и доверительные интервалы для параметров распределения. 3. Исследование статистической связи между двумя признаками выборочной совокупности (элементы корреляционного анализа). 4. Определение значимости различия между двумя выборочными совокупностями (введение в теорию статистических гипотез).
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.32.6 (0.011 с.) |

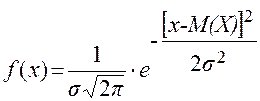 , (26)
, (26) График функции (26) называется нормальной кривой распределения (кривой Гаусса). Он имеет симметричный вид относительно ординаты х = М (Х). Максимальная плотность вероятности, равная
График функции (26) называется нормальной кривой распределения (кривой Гаусса). Он имеет симметричный вид относительно ординаты х = М (Х). Максимальная плотность вероятности, равная  »
» 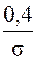 , соответствует математическому ожиданию М (Х) =
, соответствует математическому ожиданию М (Х) =  ; по мере удаления от нее плотность вероятности f (х) падает и постепенно приближается к нулю (рис. 5).
; по мере удаления от нее плотность вероятности f (х) падает и постепенно приближается к нулю (рис. 5). При изменении значения М (Х) в (26) нормальная кривая не меняется по форме, но сдвигается вдоль оси абсцисс. С возрастанием s максимальная ордината кривой убывает, а сама кривая, становясь более пологой, растягивается вдоль оси абсцисс, при уменьшении sкривая вытягивается вверх, одновременно сжимаясь с боков. Вид кривой распределения при разных значениях s:(s3<s2<s1) показан на рис.6.
При изменении значения М (Х) в (26) нормальная кривая не меняется по форме, но сдвигается вдоль оси абсцисс. С возрастанием s максимальная ордината кривой убывает, а сама кривая, становясь более пологой, растягивается вдоль оси абсцисс, при уменьшении sкривая вытягивается вверх, одновременно сжимаясь с боков. Вид кривой распределения при разных значениях s:(s3<s2<s1) показан на рис.6.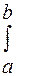 f (х) dх = 1, или
f (х) dх = 1, или  f (х) dх = 1.
f (х) dх = 1.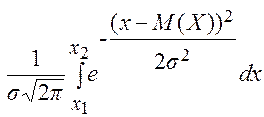 . (27)
. (27) На практике часто приходиться вычислять вероятности попадания значений нормально распределенной случайной величины на участки, симметричные относительно М (Х). В частности, рассмотрим следующую, важную в прикладном отношении задачу. Отложим от М (Х) вправо и влево отрезки, равные s, 2s и 3s (рис. 7) и проанализируем результат вычисления вероятности попадания Х в соответствующие интервалы:
На практике часто приходиться вычислять вероятности попадания значений нормально распределенной случайной величины на участки, симметричные относительно М (Х). В частности, рассмотрим следующую, важную в прикладном отношении задачу. Отложим от М (Х) вправо и влево отрезки, равные s, 2s и 3s (рис. 7) и проанализируем результат вычисления вероятности попадания Х в соответствующие интервалы: и s, можно указать интервал, в который с вероятностью Р = 99,73% попадают значения данной случайной величины. Такой способ оценки диапазона возможных значений Х известен как «правило трех сигм».
и s, можно указать интервал, в который с вероятностью Р = 99,73% попадают значения данной случайной величины. Такой способ оценки диапазона возможных значений Х известен как «правило трех сигм».


