
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории ошибок (погрешностей)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Цельюлюбого измерения некоторой физической величины является получение её истинного значения. Однако это весьма непростая задача из-за различных ошибок (погрешностей), неизбежно возникающих при измерениях. Все измерения делятся на прямые и косвенные. Прямые измерения производятся с помощью приборов, которые непосредственно измеряют исследуемую величину. При косвенных измерениях определяемую величину вычисляют по некоторой формуле, а параметры, входящие в эту формулу, находят путем прямых измерений. Погрешность, возникающая в прямых измерениях, естественно, ведет к появлению ошибки косвенно определяемой величины. Ошибки (погрешности) измерений принято делить на систематические и случайные. Систематические ошибки вносятся самим измерительным прибором. Их можно учесть, если известен класс точности данного прибора. Появление случайных ошибок обусловлено влиянием многочисленных случайных причин на результаты измерений. Эти погрешности обнаруживаются лишь при повторении процедуры измерений и приводят к получению ряда близких, но все-таки различающихся между собой значений измеряемой величины. Теория ошибок позволяет оценить величину именно случайной ошибки. Обычно предполагают, что случайная ошибка подчиняется нормальному закону распределения. Рассмотрим вначале порядок обработки результатов прямых измерений. Допустим, измеряется величина Х и мы хотим найти её истинное значение – х ист. Результатом n измерений, проведенных соответствующим прибором, является ряд её значений: х1, х2, х3,…, хn. Разность между полученным х i и истинным х ист значениями представляет собой случайную абсолютную погрешность отдельного измерения D хi = хi- х ист. Причём из теории ошибок следует, что при большом числе измерений (большом n) ошибки одной и той же величины, но разного знака встречаются одинаково часто. Посмотрим, к чему это приводит. Представим полученные нами значения х i через х ист и D хi и сложим получившиеся соотношения: х1 = хист. + D х1; х2 = хист. + D х2; ………………. хn = хист. + D хn; _____________
Отсюда найдем истинное значение измеряемой величины: xист = Поскольку при большом числе измерений n ошибки равные по величине, но разные по знаку встречаются одинаково часто, то сумма абсолютных ошибок xист = Однако при любом ограниченном количестве проведенных измерений n истинное значение х ист будет отличаться от найденного среднего арифметического значения – х ¹ х ист. –, необходимо оценить величину этого различия. К решению данного вопроса можно подойти следующим образом. В связи с влиянием случайных ошибок на результаты измерений некоторой физической величины Х ряд полученных в эксперименте её значений х1, х2, х3 …, хn можно рассматривать как выборку из генеральной совокупности, которой соответствует Полученной выборке, естественно, соответствует свое среднее арифметическое значение:
Тогда с определенной доверительной вероятностьюg можно утверждать, что х ист. лежит в доверительном интервале, построенном около D х = t g , n Следовательно х ист. = В теории ошибок величину S = называют средней квадратичной ошибкой прямо измеряемой величины х, величину D х (см. (36)) – её абсолютной ошибкой, а величину e = При косвенных измерениях искомую величину Z вычисляют по некоторой формуле Z = f(x, y), где x и y – прямо измеряемые величины. Число значений x и y, полученных при измерении каждого из них, равно n: x1, х2, х3, …., хn; у1, у2, у3, …, уn. Теперь можно найти их средние арифметические значения:
и средние квадратичные ошибки: Sx = Среднее арифметическое значение косвенно измеряемой величины вычисляют по формуле
Истинное значение Z – Z ист. лежит в доверительном интервале:
Полуширина данного интервала для нормально распределенной величины Z рассчитывается по формуле: D Z = t g , n В (43) средняя квадратичная ошибка Sz косвенно измеряемой величины, равна:
где Окончательный результат обычно записывается в виде: Z ист. = e = Пример. Рассчитаем случайную ошибку при косвенном измерении вязкости жидкости: h = h0 где h, r, t – вязкость, плотность и время истечения исследуемой жидкости из капилляра вискозиметра; h0, r0, t 0 – соответственно вязкость, плотность и время истечения эталонной жидкости (воды). Величины h0, r0 и r считаем точно известными, t и t 0 измеряем секундомером, вязкость исследуемой жидкости – косвенно измеряемая величина. 1. Пять измерений времени истечения исследуемой жидкости и воды дали следующие результаты: для исследуемой жидкости t = 79, 2с;80,4с;78,0с; 83,6с; 80,2 с; для воды t 0 = 51,0с; 48,4с; 50,6с; 47,4с; 44,2с. 2. Найдем по (39) средние арифметические значения t и t 0:
Определим по (41) среднее арифметическое значение вязкости исследуемой жидкости при: r = 790
3.Рассчитаем среднюю квадратичную ошибку вязкости по (44): Sh = Для этого по (40) определим средние квадратичные ошибки времени истечения исследуемой жидкости St и воды S t =
Найдем частные производные
Тогда S h = 4. Определим полуширину доверительного интервала или абсолютную ошибку вязкости Dh по (43). Для этого, приняв доверительную вероятность g = 0,95, и, зная число измерений непосредственно определяемых величин (n = 5), найдем коэффициент Стьюдента, [cм. табл., напр. в (4, 9)], t g, n = 2,78, тогда: Dh = 2,78 × Следовательно, с доверительной вероятностью g = 0,95 = 95% истинное значение вязкости исследуемой жидкости лежит в интервале η = Относительная ошибка равна e =
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 797; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 = nxист. +
= nxист. +  .
.

 .
. не растет с увеличением n, а лишь колеблется вблизи нуля, поэтому с увеличением n слагаемое
не растет с увеличением n, а лишь колеблется вблизи нуля, поэтому с увеличением n слагаемое 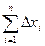 уменьшается и стремится к нулю при n ® ¥. Следовательно, при очень большом количестве измеренийистинное значение измеряемой величины практически совпадает со средним арифметическим всех полученных значений:
уменьшается и стремится к нулю при n ® ¥. Следовательно, при очень большом количестве измеренийистинное значение измеряемой величины практически совпадает со средним арифметическим всех полученных значений: .
. г = х ист. – надо найти (предполагается, и теория ошибок это подтверждает, что результаты измерений в генеральной совокупности распределены по нормальному закону).
г = х ист. – надо найти (предполагается, и теория ошибок это подтверждает, что результаты измерений в генеральной совокупности распределены по нормальному закону).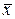 =
=  . (36)
. (36) (38)
(38)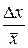 × 100 % – относительной ошибкой, оценивающей точность измерений.
× 100 % – относительной ошибкой, оценивающей точность измерений. ,
,  =
=  (39)
(39) ; Sу =
; Sу = 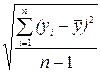 , (40)
, (40) = f (
= f (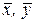 ). (41)
). (41)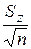 . (43)
. (43) =
=  , (44)
, (44) =Zx´ и
=Zx´ и  =Zy´ – частные производные величины Z=f (x, y), соответственно, по x и по у, вычисляемые при их средних значениях, Sx и Sу – средние квадртичные ошибки величин х и у, значения которых получаются по формулам (40).
=Zy´ – частные производные величины Z=f (x, y), соответственно, по x и по у, вычисляемые при их средних значениях, Sx и Sу – средние квадртичные ошибки величин х и у, значения которых получаются по формулам (40). × 100 %.
× 100 %. ,
, =
= 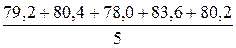 = 80,28 с,
= 80,28 с, =
=  = 48,32 с.
= 48,32 с. , r0 = 998,2
, r0 = 998,2  = h0
= h0  ;
;  = 1,31 × 10-3 Па× с = 1,31 мПа× с.
= 1,31 × 10-3 Па× с = 1,31 мПа× с. .
. :
: =2,09 с
=2,09 с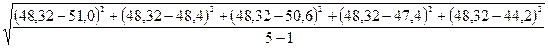 = 2,75 с.
= 2,75 с. при t =
при t =  и t 0 =
и t 0 =  0:
0: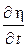 =
=  =
=  = 16,38 × 10-6 Па,
= 16,38 × 10-6 Па, = -
= -  = –
= –  = -27,21 × 10-6 Па.
= -27,21 × 10-6 Па. = 82,2 × 10-6 Па × с.
= 82,2 × 10-6 Па × с. = 0,1× 10-3 Па × с = 0,1 мПа × с.
= 0,1× 10-3 Па × с = 0,1 мПа × с. 0,1) мПа × с.
0,1) мПа × с.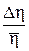 × 100 % =
× 100 % =  » 7,6 %
» 7,6 %


