
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое распределение выборкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Итак, мы хотим знать распределение признака Х в генеральной совокупности, нореально исследуем лишь некоторую выборку из нее. В серии экспериментов, проводимых с выборкой, величина Х принимает определенные значения. Эти значения записанные для всех элементов выборки в том порядке, в котором они были получены в опытах, представляет собой простой статистический ряд. Каждое значение Х в полученном числовом ряду называют вариантой. Полученные данные и подлежат статистической обработке, статистическому анализу. Первый шаг при обработке этого материала – наведение в нем определенного порядка, ведущего к получению статистического распределения выборки. Здесь возможны два основных способа: создание вариационного ряда или интервального ряда. Рассмотрим вариационный ряд. Пусть некоторая выборка исследуется по количественному признаку Х, который представляет собой дискретную случайную величину. В имеющемся у нас простом статистическом ряду варианта х 1 встречается (повторяется) m 1 раз, х 2 – m 2 раза, … х к – m краз, при этом 1) различные по значению варианты xi, расположенные в определенной, ранжированной *, заранее выбранной последовательности (обычно в порядке возрастания); 2) mi – частоты вариант, т.е. числа наблюдений (повторений) варианты х i в простом статистическом ряду; 3) pi*= mi /n – относительные частоты вариант, т.е. отношения частот mi к объему выборки n; они являются выборочными (эмпирическими) оценками вероятностей появления значений хi. Каждая относительная частота указывает долю общего объема выборки, приходящуюся на данное значение варианты хi. Итак, для дискретной величины Х вариационный ряд – статистическое распределение выборки – имеет следующий вид (табл. 1). Таблица 1.
Напомним, что под распределением дискретной случайной величины в теории вероятностейпонимается соответствие между возможными значениями случайной величины и их вероятностями; в математической статистике – соответствие между наблюдаемыми вариантами х i и их частотами или относительными частотами. Пример 1. Анализируемый показатель Х – срок лечения больного при некотором заболевании. Вариационный ряд – распределение больных по срокам лечения (объем выборки n = 26 больных) – имеет вид: Таблица 2.
Полезность подобного представления данных очевидна по следующей причине: мы получаем практически важный результат – возможность оценить более и менее вероятные значения признака. Интервальный ряд удобен тогда, когда количественный признак Х, характеризующий выборку, непрерывен, т.е. может принимать любые значения в некотором интервале. В этом случае статистическое распределение выборки (интервальный ряд) строится следующим образом. Область изменения признака (х макс – х мин) разбивают на несколько интервалов обычно равной ширины. Число интервалов k, как правило, не менее 5 и не более 25 и приближенно определяется следующими эмпирическими формулами: k = где n – объем выборки. Ширина интервалов одинакова и равна: Δ x= h = Затем вычисляют границы интервалов: х мин = х0, х1=х0 + h, х2=х1 + h, х3=х2 + h,…., х макс = хk. Поскольку некоторые варианты могут являться границей двух соседних интервалов, то, во избежание недоразумений, придерживаются следующего правила: к интервалу (a,b) относят варианты, удовлетворяющие неравенству a £ х < b. Затем для каждого интервала подсчитывают частоты m i и (или) относительные частоты рi*=mi/n попадания вариант в данный интервал. Нередко используют также плотность относительной частоты:
Данную величину можно считать выборочной (эмпирической) оценкой плотности вероятности. Рассмотренное выборочное распределение непрерывной случайной величины Х – интервальный ряд – обычно представляется в виде таблицы, имеющей, в частности, следующий вид (табл. 3). Таблица 3.
Пример 2. Анализируемый показатель Х – массы тела новорожденного. Определение массы тела 100 новорожденных показало, что минимальная масса составляет 2,7 кг, максимальная – 4,4 кг. Интервал (2,7 – 4,4) кг разбиваем на 10 равных интервалов (k =
Таблица 4.
Контроль: k =10, Обобщим изложенный выше материал. 1. Если выборка исследуется по количественному признаку Х, который представляет собой дискретную случайную величину, то статистическим распределением выборки является вариационным статистический ряд – полученные значения признака, записанные в упорядоченном виде с указанием их частот и относительных частот. 2. Если выборка исследуется по количественному признаку Х, который представляет собой непрерывную случайную величину, то статистическим распределением выборки является интервальный статистический ряд. Он включает в себя интервалы вариант, частоты попадания вариант в эти интервалы, относительные частоты, при необходимости – плотности относительных частот для этих интервалов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.163 (0.006 с.) |

 , т.е. равна объему выборки. Далее по данным простого статистического ряда строится статистическоераспределение(в медицинской литературе – вариационный ряд), которое удобно представить в виде таблицы, включающей в себя:
, т.е. равна объему выборки. Далее по данным простого статистического ряда строится статистическоераспределение(в медицинской литературе – вариационный ряд), которое удобно представить в виде таблицы, включающей в себя:
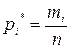






 – относительная частота
– относительная частота
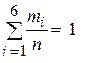
 , или k» 1 + 3,32 lg n,
, или k» 1 + 3,32 lg n,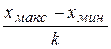 .
. =
=  .
. =10) шириной h =
=10) шириной h =  = 0,17 кг и строим интервальный ряд (табл. 4):
= 0,17 кг и строим интервальный ряд (табл. 4): mi =4+8+12+16+21+15+11+7+4+2=100= n (объем выборки),
mi =4+8+12+16+21+15+11+7+4+2=100= n (объем выборки), 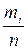 = 0,04+0,08+0,12+0,16+0,21+0,15+0,11+0,07+0,04+0,02 = 1.
= 0,04+0,08+0,12+0,16+0,21+0,15+0,11+0,07+0,04+0,02 = 1.


