
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы описательной статистикиСодержание книги Поиск на нашем сайте
Это методы описания выборок, исследуемых по количественному признаку Х, с помощью их различных числовых характеристик. Преимущество данных методов заключается в следующем. Несколько простых и достаточно информативных статистических показателей, если они известны, во-первых, избавляют нас от просмотра сотен, а порой и тысяч значений вариант, а, во-вторых, позволяют получить более или менее точную оценку характеристик распределения признака в генеральной совокупности. Описывающие выборку показатели разбиваются на несколько групп; в своем большинстве они имеют аналоги в виде числовых характеристик случайных величин в теории вероятностей. Показатели положения описывают положение вариант выборки на числовой оси. Сюда относят: а) минимальную и максимальную варианту; б) выборочное среднее арифметическое значение (выборочное среднее), выборочные моду и медиану. Они определяют «центральную» точку распределения выборки: наиболее значимую для поставленной задачи варианту. Выборочным средним называется величина
где хi – i -ая варианта, полученная в опыте с i -ым элементом выборки; n – объем выборки. Так, согласно данным табл.4 среднее выборочное значение массы тела новорожденных – Выборочная мода Мов – варианта, которая чаще всего встречается в исследуемой выборке, т.е. имеет наибольшую частоту.
Выборочная медиана Мев – варианта, которая делит ранжированный статистический ряд (см. сноску на стр. 38) на две равные части по числу попадающих в них вариант. Пример 2. Дан статистический ряд: 1; 2; 3; 3; 5; 6; 6; 6; 7; 8; 9; n = 11. Варианта, разделяющая этот ряд на две равные по количеству вариант части, занимает в ряду 6 место и равна 6, т.е. Мев = 6. Показателиразброса описывают степень разброса данных относительно своего центра. Здесь обычно используются: а) стандартное отклонение S и выборочная дисперсия Dв = S2 *, характеризующие рассеяние вариант вокруг их среднего выборочного значения
б) размах выборки – разность между максимальной и минимальной вариантами: х макс – х мин; в) коэффициент вариации: n = который применяется для сравнения величин рассеяния двух вариационных рядов: тот из них имеет большее рассеяние, у которого коэффициент вариации больше. Кпоказателям, описывающим закон распределения, прежде всего, относят гистограммы и полигон частот. О них шла речь в предыдущем разделе. 3.5. Оценка параметров генеральной совокупности по ее выборке. Точечная и интервальная оценки Напомним, что главная цель любого статистического исследования – установить закон распределения и получить значения характеристик изучаемого признака генеральной совокупности путем анализа выборки. Иначе говоря, надо определить генеральную среднюю Точечная оценка характеристик генеральной совокупности – наиболее простой, но не очень достоверный способ. При данном способе в качестве оценок характеристик генеральной совокупности используются соответствующие числовые характеристики выборки. Например, в качестве генерального среднего используется выборочное среднее, в качестве генеральной дисперсии – выборочная дисперсия и т.д. Такие оценки и называются точечными. Их недостаток состоит в том, что не ясно, насколько сильно они отличаются от истинных значений параметров генеральной совокупности. Ошибка может быть особенно большой в случае малых выборок. Интервальная оценка параметров генеральной совокупности – более достоверна. В этом случае определяется интервал, в который с заданной вероятностью попадает истинное значение исследуемого признака. Такой интервал называется доверительным интервалом, а вероятность того, что истинное значение оцениваемой величины находится внутриэтого интервала – доверительнойвероятностью или надежностью. В медицинской литературе для этой величины используется термин «вероятность безошибочного прогноза». Обозначим ее g. Значения g задаются заранее (обычно в медико-биологических исследованиях выбирают значения g = 0,95 = 95% или g = 0,99 = 99%), после чего находят соответствующий доверительный интервал*. Для построения надежных интервальных оценок необходимо знать закон, по которому оцениваемый случайный признак распределен в генеральной совокупности. Рассмотрим, вначале для малых выборок (n < 30), как строится интервальная оценка генеральнойсредней
или, в другой форме записи: Мг (Х) = где d = t g , n× (S/ Анализ формулы (34) показывает, что: а) чем больше доверительная вероятность g, тем больше коэффициент t g ,n и шире доверительный интервал; б) чем больше объем выборки n, тем уже доверительный интервал. При большой выборке (n > 30) полуширину доверительного интервала d определяют по соотношениям: d = 1,96 S/ Доверительный интервал существует и для s г. Здесь мы его не приводим. Подобные интервальные оценки с заданной надежностью даются и в тех случаях, когда рассматриваемый случайный признак распределен в генеральной совокупности не по нормальному, а по другим законам. Пример. Исследуется состояние дыхательных путей курящих. В качестве характеристики используется показатель функции внешнего дыхания – максимальная объемная скорость середины выдоха. Предполагая, что в генеральной совокупности данный параметр распределен по нормальному закону, найдите 95%-ный и 99%-ный доверительные интервалы для Решение: 1. Для g = 95% и n = 20 находим по таблицам коэффициент Стьюдента ** d = t g , n × (S/ Теперь можем записать доверительный интервал для Мг (Х): (2,2 – 0,342) л/с < Мг (Х) < (2,2 + 0,342) л/с, т.е. 1,858 л/с < Мг (Х) < 2,542 л/с. В более компактной эквивалентной форме записи: Мг (Х) = (2,2 ± 0,342) л/с. 2. Для g = 99% и n = 20 t 0,99;20 = 2,86; тогда Мг (Х) = (2,2 – 0,467) л/с < Мг (Х) < (2,2 + 0,467) л/с или 1,733 л/с < Мг (Х) < 2,667 л/с, иначе Мг (Х) = (2,2 ± 0,467) л/с. Полученные данные подтверждают ранее сделанный вывод: увеличение доверительной вероятности g «раздвигает» границы доверительного интервала. Из формулы (34) понятно, как по заданной доверительной вероятности и объему выборки получить точность оценки Мг (Х) = Поставим обратную, практически значимую задачу. По заданной точности оценки d, т. е. по заданной полуширине доверительного интервала, определим необходимый объем выборки, обеспечивающий нужное d. Эта задача решается особенно просто в случае больших выборок (n > 30). Здесь, например, при доверительной вероятности 95 % d = 1,96 × S / n ³ (1,96)2 S 2/d2 Пример 2. Исследователь хочет установить средний уровень гемоглобина для определенной группы населения. Учитывая предварительные данные, он полагает, что этот уровень составляет примерно 150 г/л со стандартным отклонением 32 г/л. Определите, сколько человек он должен обследовать (с какой выборкой он должен работать) при d= 5 г/л. и доверительной вероятности 0,95 = 95 %. Решение: n = (1,96)2 × 322/52 = 157,4. Таким образом, необходимо обследовать не менее 158 человек.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 706; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.78 (0.009 с.) |

 в =
в = 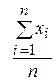 , (31)
, (31) Пример 1. На рис. 10 приведено предполагаемое распределение по возрасту заболевших дифтерией (на 10 тыс. населения соответствующего возраста), которое явно не соответствует нормальному. Очевидно, что знание среднего возраста заболевших (
Пример 1. На рис. 10 приведено предполагаемое распределение по возрасту заболевших дифтерией (на 10 тыс. населения соответствующего возраста), которое явно не соответствует нормальному. Очевидно, что знание среднего возраста заболевших ( ; (32)
; (32) × 100%, (33)
× 100%, (33) г = М (Х), генеральные дисперсию Dг (Х), среднее квадратическое отклонение sг, генеральную моду Мог, медиану Мег и другие характеристики генеральной совокупности путем статистического исследования выборки.
г = М (Х), генеральные дисперсию Dг (Х), среднее квадратическое отклонение sг, генеральную моду Мог, медиану Мег и другие характеристики генеральной совокупности путем статистического исследования выборки. ) – полуширина доверительного интервала (точность оценки); n – объем выборки; S – выборочное среднее квадратическое отклонение;
) – полуширина доверительного интервала (точность оценки); n – объем выборки; S – выборочное среднее квадратическое отклонение;  ) = 2,09 ×
) = 2,09 ×  = 0,342.
= 0,342. и, следовательно, необходимый объем выборки равен:
и, следовательно, необходимый объем выборки равен:


