
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тепловой эффект химической реакции не зависит от пути её протекания, А зависит только от природы и состояния исходных веществ и конечных продуктов реакции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если из данных исходных веществ можно различными способами получить заданные конечные продукты, то независимо от путей получения (независимо, например, от промежуточных стадий процесса) суммарный тепловой эффект будет одним и тем же, то есть тепловой эффект образования заданных продуктов из данных реагентов не зависит от числа и вида реакций, в результате которых образуются эти продукты. Например, процесс превращения исходных веществ А и В в конечные продукты Д и Е представлен двумя путями: 1 путь – непосредственное превращение А и В в продукты Д и Е в одну стадию, тепловой эффект которой равен ∆Н1. 2 путь – конечные продукты Д и Е получаются из реагентов А и В в несколько стадий, тепловые эффекты которых равны ∆Н2, ∆Н3 и ∆Н4. Закон Гесса утверждает, что тепловые эффекты будут связаны между собой таким соотношением:
то есть независимо от пути получения веществ Д и Е из исходных веществ А и В суммарный тепловой эффект для двух путей будет одним и тем же. Закон Гесса строго соблюдается только для процессов, протекающих при постоянном объеме системы (V = const) или при постоянном давлении (р = const). При этом предполагается, что температура исходных веществ и продуктов реакции тоже одинакова (T = const) и что система не совершает никакой другой работы, кроме работы расширения против внешнего давления, связанной с изменением объема системы (при р = const). Таким образом, закон Гесса справедлив для изобрано-изотермических процессов (Т = const, p = const) и изохорно-изотермических процессов (Т=const, V = const). Как уже известно, для изобарных процессов тепловой эффект равен изменению энтальпии процесса ∆Н, а для изохорного процесса он равен изменению внутренней энергии ∆Е. Так как Н и Е являются термодинамическими функциями состояния системы, то их изменения ∆Н и ∆Е не зависят от пути процесса, поэтому и тепловой эффект реакции тоже не зависит от пути процесса, а определяется лишь начальным и конечным состоянием веществ, о чем и свидетельствует закон Гесса. Важно еще раз подчеркнуть, что применять закон Гесса можно лишь тогда, когда для всех путей химического процесса должны быть одинаковы начальные и конечные состояния веществ. При этом одинаковыми должны быть не только химические составы веществ, но и условия их существования (температура, давление) и агрегатные состояния, а для кристаллических веществ одинаковы также аллотропные видоизменения. Закон Гесса позволяет рассчитать тепловые эффекты химических реакций, которые трудно экспериментально определить.
Закон Гесса строго соблюдается как в живых, так и в неживых системах. Например, 1 грамм жиров, углеводов или белка при окислении в организме и при сгорании в калориметре выделяет следующее количества теплоты (Дж):
В организме белки окисляются не до конца, а до мочевины, воды и СО2, поэтому выделяется при окислении 1 грамма белка меньше теплоты, чем при сгорании 1 грамма белка в калориметре, в котором окисление белка происходит до конечных продуктов окисления, поэтому количество выделяющейся теплоты немного больше. При термохимических расчетах чаще применяется не сам закон Гесса, а его следствия. Наиболее важные из них используют теплоты образования и теплоты сгорания веществ для определения тепловых эффектов химических реакций.
Тепловые эффекты реакций можно включать в уравнения реакций. В термохимии используют термохимические уравнения реакций. Уравнения химических реакций, записанные с указанием теплового эффекта, называют термохимическими уравнениями реакций. Тепловой эффект реакции зависит от природы реагирующих веществ и их агрегатных состояний, а также от аллотропных видоизменений твердых веществ (алмаз, графит, карбин и др.), поэтому в термохимических уравнениях отмечают состояние веществ: (к) – кристаллическое, (ж) – жидкое, (г) – газообразное, (р) – растворенное и др. Если специально не оговорено, то тепловой эффект приводится для стандартной температуры (298 К) и стандартного давления (101,3 кПа). Тепловой эффект реакции в приведенном примере записан термохимическим способом, в котором теплота (Q) считается положительной, если она выделяется во внешнюю среду, если же она поглощается извне (для эндотермических реакций), то тепловой эффект считается отрицательным: N2(г) + О2(г) = 2NO(г) – 180,8 кДж. Термодинамическая запись теплового эффекта осуществляется посредством изменения энтальпии реакции ∆Н. При этом положительной теплотой считают теплоту, которую система получает от окружающей среды, то есть для эндотермических реакций, для которых ∆Н > 0, отрицательной теплотой считается теплота, которая выделяется системой в окружающую среду, то есть для экзотермических реакций, для которых ∆Н < 0. Значение ∆Н реакции (в кДж) в термохимических уравнениях указывают после уравнения реакции (через точку с запятой): Н2(г) + Cl2(г) = 2HCl(г); ∆Но298 = -183,2 кДж, N2(г) + О2(г) = 2NO(г); ∆Но298 = +180,8 кДж. С термохимическими уравнениями можно производить все алгебраические действия: сложение, вычитание, умножение.
При расчетах тепловых эффектов химических реакций на основе закона Гесса используются энтальпии образования и энтальпии сгорания веществ. Энтальпия (теплота) образования вещества – это тепловой эффект реакции образования 1 моль данного вещества из простых веществ, устойчивых при 298 К и 101,3 кПа. Например, энтальпией образования глюкозы будет тепловой эффект реакции: 6С(к) + 3О2(г) + 6Н2(г) = С6Н12О6(к) Не всегда энтальпию образования вещества можно определить непосредственно. Так, нельзя провести приведенную реакцию получения глюкозы. Закон же Гесса дает возможность вычислить ∆Н этой реакции из энтальпий других химических реакций. Обычно используют стандартные энтальпии (теплоты) образования веществ, по которым рассчитывают стандартные тепловые эффекты реакций (∆Но298). Их обозначают ∆Нообр 298. Стандартные энтальпии образования простых веществ, устойчивых в стандартных условиях (газообразный О2, жидкий бром, кристаллический йод, ромбическая сера, графит и др.) равны нулю. Энтальпии образования относят к 1 моль вещества, указывая его агрегатное состояние. Для многих веществ стандартные теплоты образования известны и сведены в справочные таблицы. Составление таких таблиц позволяет путем комбинации нескольких сот известных веществ рассчитывать тепловые эффекты для десятков тысяч реакций, не прибегая к эксперименту. Пользуясь табличными данными ∆Нообр, 298 веществ, участвующих в данной реакции, можно на основании закона Гесса рассчитать тепловой эффект реакции при стандартных условиях (∆Но298). Стандартный тепловой эффект реакции (стандартная энтальпия реакции) равен разности между алгебраической суммой стандартных энтальпий образования продуктов реакции и алгебраической суммой стандартных энтальпий образования исходных веществ, умноженных на соответствующие стехиометрические коэффициенты перед формулами веществ в химическом уравнении реакции. Для реакции, представленной в общем виде аА + вВ = dД + еЕ стандартный тепловой эффект ∆Но298 определяется равенством: ∆Но298 = (d•∆Hof, Д + е•∆Ноf, E) – (a•∆Hof, A + в•∆Ноf, B) (1.8).
Пример 1. Рассчитайте стандартный тепловой эффект реакции С6Н12О6(к) + 6О2(г) = 6СО2(г) + 6Н2О(ж) по стандартным теплотам образования веществ. Решение. Из таблиц находят ∆Ноf, 298 в кДж/моль каждого вещества:
Согласно уравнению (1.8.) ∆Но298 =
= -6•393,5 - 6•286 – (-1260) = -2817 кДж - (реакция экзотермическая)
Теплотой (энтальпией) сгорания вещества называют тепловой эффект реакции сгорания (окисления) в атмосфере кислорода 1 моль вещества до образования его конечных продуктов окисления (СО2(г), Н2О(ж), продукты окисления остальных элементов определяются конкретно в каждом случае). Для расчета тепловых эффектов реакций обычно используют стандартные теплоты (энтальпии) сгорания веществ, которые обозначают ∆Нос. 298 Продуктами сгорания при стандартных условиях являются СО2(г), Н2О(ж), SO2(г), N2(г) и др. Стандартные теплоты сгорания устойчивых оксидов приняты за нуль. Для многих веществ (особенно органических веществ) стандартные теплоты сгорания известны и сведены в справочные таблицы. Отметим, что если теплоты сгорания всех веществ отрицательны, то теплоты образования веществ не всегда имеют отрицательное значение. Известны вещества, образование которых связано с поглощением теплоты. Пользуясь табличными данными ∆Нос. 298 веществ, участвующих в данной реакции, можно рассчитать на основании закона Гесса тепловой эффект реакции при стандартных условиях (∆Но298). Стандартный тепловой эффект реакции (стандартная энтальпия реакции) равен разности между алгебраической суммой стандартных энтальпий сгорания исходных веществ и алгебраической суммой стандартных энтальпий сгорания продуктов реакции, умноженных на соответствующие стехиометрические коэффициенты в химическом уравнении реакции. Для реакции аА + вВ = dД + еЕ стандартная энтальпия ∆Но298 определяется равенством: ∆Но298 = (а•∆Hoс, А + в•∆Нос, В) – (d•∆Hoс, Д + е•∆Нос, Е) (1.9).
Пример 2. Рассчитайте стандартный тепловой эффект реакции СН4(г) + СО2(г) = 2СО(г) + 2Н2 по стандартным теплотам сгорания веществ. Решение. Из таблиц находят стандартные теплоты сгорания ∆Нос. 298 в кДж/моль каждого вещества:
Согласно уравнению (1.9) ∆Но298 =
= -802,3 – (-2•283,0) – (-2•241,8) = +247,3 кДж (реакция эндотермическая)
Термохимические расчеты для реакций в растворах целесообразно проводить не по теплотам образования молекул (химических соединений), а по теплотам образования ионов. Однако измерить теплоты образования для отдельных ионов невозможно, так как ионам одного знака всегда сопутствуют ионы противоположного знака. Поэтому условились для ионов ввести начало отсчета, приняв теплоту образования иона Н+ за нуль, то есть ∆Ноf, 298, H+(p) = 0. Используя эту величину и зная суммы ∆Ноf, 298 для положительных и отрицательных ионов, находят теплоты образования ∆Ноf отдельных ионов в растворе. Стандартные теплоты образования ионов в водном растворе сведены в справочные таблицы. Пример 3. Рассчитайте стандартный тепловой эффект реакции KBr + AgNO3 = AgBr↓ + KNO3 или Br−(p) + Ag+(p) = AgBr(k) Решение. Из таблиц находят ∆Ноf, 298 в кДж/моль: ∆Ноf, AgBr(k) = -100,7; ∆Ноf, Ag+(p) = +106,0; ∆Ноf, Br-(p) = -122,0. Согласно уравнению (1.8) ∆Но298 = ∆Ноf, AgBr(k) - ∆Ноf, Ag+(p) - ∆Ноf, Br-(p) = -100,7 – 106,0 – (-122,0) = -84,7кДж
4. Второй закон термодинамики. Энтропия. Стандартные энтропии веществ. Энергия Гиббса.
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. В замкнутой системе (которая ни с чем не взаимодействует) степень "упорядоченности" может либо уменьшаться, либо быть неизменной. Отсюда следствие: энергия от более холодных частей замкнутой системы к более горячим передаваться не может, а вот наоборот - сколько угодно. До тех пор, пока температура во всей системе не выровняется, и "упорядоченность" исчезнет.
Помимо внутренней энергии и энтальпии существует ещё одна функция состояния, изменение которой в совокупности с изменением одной из первых двух определяет возможность или невозможность самопроизвольного протекания процесса. Такой функцией состояния, а также мерой упорядоченности, или вероятности состояния, системы является энтропия (S). Энтропия, измеряемая в тех же единицах, что и теплоёмкость, Дж/(моль*К), является таким же свойством вещества или системы, зависящим от их природы и состояния, как температура, давление, внутренняя энергия и энтальпия. Каждому состоянию данной термодинамической системы соответствует определённое значение энтропии, которое тем выше, чем больше вероятность данного состояния системы. Энтропия есть мера неупорядоченности (беспорядка) состояния системы или мера вероятности нахождения системы в данном состоянии – это молекулярно-кинетическое определение энтропии. Частицам (молекулам, атомам, ионам) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное состояние, при этом энтропия системы увеличивается. Чем больше неупорядоченность системы, тем больше численное значение энтропии, а значит это состояние системы будет наиболее вероятным. Энтропии веществ, как и их энтальпии образования, принято относить к температуре 298 К и давлению 101,3 кПа. Энтропию веществ при этих условиях обозначают So298 и называют стандартной энтропией. Значения стандартной энтропии веществ сведены в справочные таблицы. Энтропии простых веществ (О2, Н2 и др.) не равны нулю и тоже приводятся в справочных таблицах. Энтропии веществ имеют сравнительно небольшие значения – порядка десятков или сотен Дж/моль•К. Подобно внутренней энергии и энтальпии, энтропия зависит только от состояния системы, то есть является функцией состояния. Но в отличие от внутренней энергии и энтальпии могут быть определены абсолютные значения энтропии веществ, так как при температуре 0 К энтропии кристаллических веществ равны нулю. Существуют некоторые закономерности в изменении энтропии веществ. Так, энтропия вещества в газообразном состоянии значительно больше, чем в жидком состоянии, а в жидком состоянии больше, чем в твердом состоянии (на 1 моль вещества). Например, So298H2O(г) = 188,6; So298H2O(ж) = 70,0; So298Н2О(т) = 44,1 Дж/моль•К. При одинаковом агрегатном состоянии вещества энтропии тем больше, чем больше атомов содержится в молекуле, то есть усложнение молекулы приводит к возрастанию энтропии. Так, So298O3(г) = 238,7; So298O2(г) = 205,0; So298O(г) = 160,8 Дж/моль•К. Это объясняется тем, что у атомарного кислорода (О) возможно только поступательное движение частиц; у молекул О2 возможно и поступательное, и вращательное, и колебательное движение, а у угловых молекул О3 набор вращательных и колебательных движений возрастает. Возрастание энтропии с усложнением молекул происходит также для жидких и твердых веществ. Энтропия вещества в аморфном состоянии больше, чем в кристаллическом (более упорядоченном) состоянии: для SiO2 соответственно равны 46,9 и 42,8 Дж/моль•К. Чем больше твердость и жесткость вещества, тем меньше его энтропия. Например, для графита и алмаза стандартные энтропии соответственно равны 5,68 и 2,42Дж/моль•К. Используя табличные значения So298 веществ, участвующих в данной химической реакции, можно на основании закона Гесса определить изменение энтропии реакции при стандартных условиях. Изменение энтропии реакции равно разности между алгебраической суммой энтропий продуктов реакции и алгебраической суммой энтропий исходных веществ, умноженных на соответствующие стехиометрические коэффициенты в химическом уравнении реакции. Так, для химической реакции в общем виде аА + вВ = dД + еЕ изменение энтропии будет равно: ∆ So298 = (d• So298, Д + е• So298, Е) – (а• So298, А + в• So298, В) (1.12). Об изменении энтропии в химической реакции можно судить по изменению объема системы в ходе реакции. Например, в реакции 3Н2(г) + N2(г) = 2H3N(г) объем системы уменьшается (∆V < 0), поэтому энтропия тоже уменьшается (∆S < 0).
Самопроизвольному протеканию химической реакции в прямом направлении способствует сочетание условий ∆Н < 0 и ∆S или (Т•∆S) > 0. При этом следует иметь в виду, что энтальпийный фактор ∆Н обычно мало зависит от температуры, а энтропийный фактор Т•∆S увеличивается с повышением температуры. Если химический процесс протекает без изменения энтропии, то есть ∆S ≈ 0 (например, реакция нейтрализации происходит при смешивании очень разбавленных растворов HCl и КОН), то движущей силой самопроизвольного протекания этого процесса является уменьшение энтальпии (∆Н<0). Если же химический процесс протекает без изменения энтальпии (∆Н ≈ 0), то движущей силой этого процесса является энтропийный фактор, то есть процесс самопроизольно может протекать в направлении увеличения энтропии (Т • ∆S > 0). Однако такие реакции осуществляются редко и большинство реакций сопровождается одновременным изменением как энтальпии, так и изменением энтропии (∆Н ≠ 0, ∆S ≠ 0). В этом случае действие обоих факторов (∆Н и Т•∆S) на возможность и направление протекания процесса учитывает изменение новой функции состояния – энергии Гиббса, названной в честь американского физика Д.Гиббса, который ввел эту функцию в термодинамику и использовал её в своих работах: ∆G = ∆H – T•∆S (1.13) Энергия Гиббса(G) или изобарно-изотермический потенциал является движущей силой химических процессов, протекающих при p = const и T = const, а изменение энергии Гиббса ∆G служит критерием самопроизвольного протекания изобарно-изотермических реакций (то есть реакций, протекающих при постоянной температуре и постоянном давлении), а именно: · при постоянстве температуры и давления в системе самопроизвольно может протекать только такая химическая реакция, в результате которой энергия Гиббса системы уменьшается, а изменение энергии Гиббса реакции ∆G < 0. Таким образом, изобарно-изотермические реакции протекают самопроизвольно в таком направлении, при котором энергия Гиббса уменьшается, то есть энергия Гиббса системы в исходном состоянии больше, чем в конечном состоянии. · Если для реакции ∆G < 0, то данная реакция возможна в прямом направлении. · Если ∆G > 0, то есть энергия Гиббса увеличивается, то при данных условиях самопроизвольное протекание реакции в прямом направлении невозможно, и данная реакция возможна в обратном направлении. · Если ∆G = 0, то наступило состояние термодинамического равновесия (для химической реакции – состояние химического равновесия), то есть изменение энергии Гиббса происходить не будет и G1=G2 = const. При этом из уравнения (1.13) следует, что при наступлении равновесия, когда ∆G = 0, энтальпийный и энтропийный факторы (∆Н и Т•∆S) компенсируют друг друга и справедливо равенство ∆Н = Т•∆S Для химической реакции это равенство отвечает равновесию между исходными веществами и продуктами химической реакции, при этом скорости прямой и обратной реакции становятся равными. Таким образом, изменение энергии Гиббса ∆G реакции указывает: o на возможность протекания химической реакции при данных условиях, o на направление самопроизвольного химического процесса, o на предел протекания химического процесса: чем отрицательнее значение ∆G, тем сильнее и глубже протекает реакция в прямом направлении, то есть дальше находится система от состояния химического равновесия и тем более она реакционноспособна и степень превращения исходных веществ в продукты реакции больше. o С помощью такого критерия, как ∆G реакции, можно определить также, как влияет на течение процесса температура, давление, варьирование концентрации реагентов, можно ли создать условия, при которых данное вещество может реагировать с другими веществами, можно ли заставить изучаемую реакцию протекать в обратном направлении и др. Необходимо отметить, что отрицательное значение ∆G реакции указывает лишь на возможность её протекания, а в действительности реакция может при этом не протекать. Если скорость такой реакции будет ничтожно мала, тогда она практически протекать не будет, хотя она возможна при данных условиях, так как ∆G < 0. Такое положение часто возникает при низких температурах. В этом случае для увеличения скорости реакции подбирают подходящий катализатор. Учитывая уравнение (1.13), можно разобрать несколько частных случаев. Если химический процесс протекает с уменьшением энтальпии (∆Н < 0) и увеличением энтропии (∆S > 0), то в этом случае и энтальпийный, и энтропийный факторы способствуют самопроизвольному протеканию реакции в прямом направлении. Подставляя данные условия в уравнение (1.13), получают, что ∆G всегда будет меньше нуля, то есть возможен химический процесс только в прямом направлении. Действительно, все экзотермические реакции, для которых ∆Н < 0, протекающие с увеличением энтропии (∆S > 0), являются необратимыми. Например, 2KClO3(к) ∆Но298 = -89,4 кДж; ∆So298 = 493,4 Дж/К Если оба фактора не способствуют протеканию реакции в прямом направлении (∆Н > 0, ∆S < 0), то ∆G всегда будет больше нуля и возможно протекание реакции только в обратном направлении. Если энтальпийный фактор способствует протеканию реакции в прямом направлении (∆Н < 0), а энтропийный фактор благоприятствует протеканию реакции в обратном направлении (∆S < 0), в этом случае ∆G реакции может иметь и положительное, и отрицательное значение, в зависимости от того, какое из слагаемых в уравнении (1.13) больше по абсолютной величине: ∆Н или Т∆S. Реакция возможна в прямом направлении (∆G < 0), если │∆H│>│T∆S│, то есть возможность этой реакции определяется действием энтальпийного фактора, которое перекрывает противодействие энтропийного фактора. Если ∆Н > 0 и ∆S > 0, то есть факторы снова противодействуют, то возможность этой реакции, наоборот, определяется действием энтропийного фактора. Реакция будет протекать самопроизвольно в прямом направлении (∆G < 0), когда энтропийный фактор перекрывает энтальпийный фактор, то есть │T∆S│ > ∆H. В этом случае повышение температуры будет благоприятствовать самопроизвольному протеканию реакции. Подобно энтальпиям образования веществ используют энергии Гиббса образования веществ, которые применяются для расчета изменения энергии Гиббса химических реакций. Энергия Гиббса образования вещества – это изменение энергии Гиббса реакции образования 1 моль вещества из простых веществ. Обозначается ∆Gof 298 и относится к 1 моль вещества при стандартных условиях, обычно выражается в кДж/моль. При этом, стандартная энергия Гиббса образования простого вещества, устойчивого в стандартных условиях, равна нулю. Для многих веществ ∆Gof,298 известны и сведены в справочные таблицы. Пользуясь табличными данными ∆Gof, 298 веществ, участвующих в данной реакции, можно на основании закона Гесса рассчитать изменение энергии Гиббса реакции (или энергию Гиббса реакции) при стандартных условиях. Стандартная энергия Гиббса реакции (стандартное изменение энергии Гиббса реакции) равна разности между алгебраической суммой стандартных энергий Гиббса образования продуктов реакции и алгебраической суммой стандартных энергий Гиббса образования исходных веществ, умноженных на соответствующие стехиометрические коэффициенты в химическом уравнении реакции. Для реакции, представленной в общем виде аА + вВ = dД + еЕ стандартная энергия Гиббса определяется равенством: ∆Go298 = (d•∆Gof,Д + е•∆Gof, Е) – (а•∆Gof, A + в•∆Gof, В) (1.14). С помощью энергий Гиббса образования биогенных веществ на основе закона Гесса (уравнение 1.14) можно определять энергии Гиббса биохимических реакций и прогнозировать их протекание в живых организмах. Поэтому ∆G реакций может использоваться для энергетической характеристики химических превращений аналогично изменению энтальпии ∆Н. Уравнения реакций, для которых указывается соответствующее этим реакциям изменение энергии Гиббса, также называются термохимическими уравнениями. Например: С6Н12О6(к) + 6О2(г) = 6СО2(г) + 6Н2О(ж), ∆Go298 = -2880 кДж. Химические реакции, при протекании которых происходит уменьшение энергии Гиббса (∆G < 0), называются экзергоническими реакциями. Реакции, в результате которых энергия Гиббса возрастает (∆G>0), называется эндергоническими реакциями (такие реакции самопроизвольно протекать не могут).
5. Термодинамические условия равновесия. Критерии направления самопроизвольно протекающих процессов. Энтальпийный и энтропийный факторы. Экз- и эндэргонические процессы в организмах. Гидролиз АТФ как универсальный источник энергии в организме. Принцип энергетического сопряжения.
Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура,давление, объём, энтропия) в условиях изолированности от окружающей среды. Эти величины не являются постоянными, они лишь колеблются возле своих средних значений. Термодинамические условия равновесия: · Постоянство давления Р во всех точках системы, означающее установление механического равновесия. · Постоянство температуры Т во всех точках системы, означающее установление теплового равновесия. Это условие означает отсутствие тепловых, т.е. энергетических, потоков в системе на молекулярном уровне. · Третье условие термодинамического равновесия должно отражать отсутствие потоков массы на молекулярном уровне, и по физическому смыслу может быть сформулировано как равенство нулю средних скоростей (не тепловых) движения молекул или как отсутствия явления молекулярной диффузии. В простейших случаях в отсутствие силовых полей, фазовых переходов и химических реакций третьим условием равновесия будет постоянство концентраций веществ во всей системе.
o При постоянстве температуры и давления в системе самопроизвольно может протекать только такая химическая реакция, в результате которой энергия Гиббса системы уменьшается, а изменение энергии Гиббса реакции ∆G < 0. o Если химический процесс протекает с уменьшением энтальпии (∆Н < 0) и увеличением энтропии (∆S > 0), то в этом случае и энтальпийный, и энтропийный факторы способствуют самопроизвольному протеканию реакции в прямом направлении. o Если ∆Н > 0 и ∆S > 0, то есть факторы снова противодействуют, то возможность этой реакции, наоборот, определяется действием энтропийного фактора. Реакция будет протекать самопроизвольно в прямом направлении (∆G < 0), когда энтропийный фактор перекрывает энтальпийный фактор, то есть │T∆S│ > ∆H. В этом случае повышение температуры будет благоприятствовать самопроизвольному протеканию реакции.
Любой процесс, в том числе и химическая реакция, протекает самопроизвольно, то есть без затраты энергии извне, если система при этом переходит из менее устойчивого состояния в более устойчивое. При протекании химической реакции одновременно действуют две противоположные тенденции: с одной стороны частицы за счет образования связей стремятся объединиться в более сложные частицы (например, атомы объединяются в молекулы, а молекулы в более крупные агрегаты), что приводит к выделению энергии и уменьшению энтальпии (∆Н<0); с другой стороны частицы стремятся разъединиться и в результате теплового движения беспорядочно распределиться по всему объему системы, что приводит к увеличению энтропии системы (∆S > 0). Каждая из этих противоположных тенденций, выражаемых величинами ∆Н и ∆S, зависит от природы реагирующих веществ и условий протекания реакции (температура, давление, соотношение концентраций реагентов и др.). Таким образом, возможность и направление самопроизвольного протекания химической реакции определяется действием двух прямо противоположных факторов: энтальпийного фактора (∆Н) и энтропийного фактора (Т•∆S). Количественно оба фактора выражаются в единицах энергии (Дж или кДж). Чем выше температура Т, тем больше произведение Т•∆S, то есть сильнее энтропийный фактор. v Если изменение энтальпии химической реакции ∆Н < 0, то энтальпийный фактор способствует самопроизвольному протеканию реакции в прямом направлении, а если ∆Н > 0, то энтальпийный фактор способствует самопроизвольному протеканию реакции в обратном направлении. v Если изменение энтропии химической реакции ∆S > 0, а значит произведение Т•∆S > 0, то энтропийный фактор способствует самопроизвольному протеканию реакции в прямом направлении, а если ∆S<0, то Т•∆S < 0 и, следовательно, энтропийный фактор будет способствовать протеканию химического процесса в обратном направлении.
Химические реакции, при протекании которых происходит уменьшение энергии Гиббса (∆G < 0), называются экзэргоническими реакциями. Реакции, в результате которых энергия Гиббса возрастает (∆G>0), называется эндэргоническими реакциями (такие реакции самопроизвольно протекать не могут). Процесс окисления глюкозы дикислородом, сопровождается уменьшением энергии Гиббса и является ярким примером экзэргонической реакции в организме человека. Так как этот процесс происходит при физической нагрузке. В биологических системах термодинамически невыгодные (эндэргонические) реакции могут протекать лишь за счёт энергии экзэргонических реакций. Такие реакции называют энергетически сопряжёнными. Многие из этих реакций происходят при участии аденозинтрифосфата (АТФ), играющего роль сопрягающего фактора. Реакция фосфорилирования глюкозы свободным фосфатом с образованием глюкозо-6-фосфата является эндэргонической. Для протекания такой реакции в сторону образования глюкозо-6-фосфата необходимо её сопряжение с другой реакцией, величина свободной энергии которой больше, чем требуется для фосфорилирования глюкозы.
АТФ относится к так называемым макроэргическим соединениям, то есть к химическим соединениям, содержащим связи, при гидролизе которых происходит освобождение значительного количества энергии. Гидролиз макроэргических связей молекулы АТФ, сопровождаемый отщеплением 1 или 2 остатков фосфорной кислоты, приводит к выделению, по различным данным, от 40 до 60 кДж/моль. АТФ + H2O → АДФ + H3PO4 + энергия АДФ + H2O → АМФ + H3PO4 + энергия Высвобождённая энергия используется в разнообразных процессах, протекающих с затратой энергии. АТФ служит непосредственным источником энергии для множества энергозатратных биохимических и физиологических процессов. Всё это реакции синтеза сложных веществ в организме: осуществление активного переноса молекул через биологические мембраны, в том числе и для создания трансмембранного электрического потенциала; осуществления мышечного сокращения.
Расчёт изменения энергии Гибса позволяет сделать вывод о том, возможен или невозможен самопроизвольный процесс в данных условиях. Однако полученное положительное значение ∆G ещё не означает, что процесс невозможен в принципе. Просто для его осуществления необходима затрата дополнительной энергии. Например, для процесса фотосинтеза 6CO2(г) + 6H2O(ж)→С6H12O6(aq) + 6O2(г) -394,39 -237,14 -916,97 0 ∆rG0 298 =-916,97-(-394,39*6-237,14*6)=2872,81 кДж, а необходимая для протекания реакции энергия поставляется в виде солнечного света. Подобно фотосинтезу большинство биосинтетических процессов являются эндэргоническими, т.е. требуют затраты энергии. Значительная часть этой энергии поставляется так называемыми макроэргическими соединениями. Макроэргическими называют вещества, при гидролитическом расщеплении которых выделяется значительное количество энергии.(АТФ) Типичным примером биохимического термодинамического сопряжения может служить происходящее в растениях образование сахарозы из глюкозы и фруктозы. Эта реакция эндэргоническая и самопроизвольно в стандартных условиях протекать не может; она должна быть сопряжена с экзэргоническими реакциями, в результате которых выделяется энергия, необходимая для её осуществления.
6. Характеристика химического равновесия. Константа химического равновесия и способы её выражения: Кс, Кр, Ка. Примеры. Уравнение изотермы химической реакции.
Обратимые по направлению химические реакции – это реакции, которые при данных внешних условиях могут одновременно и самопроизвольно протекать и в прямом, и в обратном направлениях. Обратимые реакции протекают не до конца и ни одно из реагирующих веществ не расходуется полностью, так как наряду с расходованием реагирующего вещества по прямой реакции будет одновременно происходить его образование по обратной реакции. Обратимая химическая реакция заканчивается в конечном итоге установлением химического равновесия между исходными веществами и продуктами реакции. Признаки необратимости химических реакции: · Образование нерастворимого осадка · Выделение газа · Образование слабого электролита · Образование прочных комплексов · Выделение большого количества тепла Самопроизвольное протекание обратимой химической реакции происходит до установления в системе химического равновесия, при котором энергия Гиббса системы постоянна, а изменение энергии Гиббса реакции ∆Gр-я = 0. Рассмотрим обратимую химическую реакцию: Н2 + I2 ↔ 2HI. На рис.2.1. показано изменение скоростей прямой реакции Н2 + I2 ↔ 2HI и обратной реакции 2HI → H2 + I2 с течением времени t.
Рис. 2.1. Изменение скоростей прямой (V1) и обратной (V2) реакций с течением времени.
В начальный момент времени при смешении исходных веществ Н2 и I2, скорость прямой реакции определяется их начальными концентрациями и будет велика, а скорость обратной реакции равна нулю, так как концентрация продукта реакции HI в начальный момент времени равна нулю. По мере протекания реакции исходные вещества Н2 и I2 расходуются и их концентрации уменьшаются, в результате этого уменьшается и скорость прямой реакции (V1). Одновременно появляется продукт реакции HI, концентрация которого с течением времени увеличивается, поэтому и скорость обратной реакции (V2) увеличивается. Когда скорости прямой и обратной реакций стано
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2808; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.36 (0.015 с.) |



 = -1260,
= -1260, 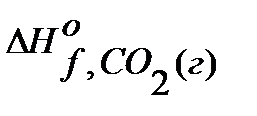 = -393,5,
= -393,5, = -286,
= -286, 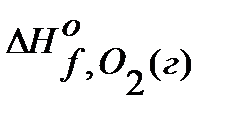 = 0
= 0 +
+  -
-  =
=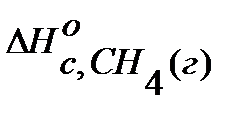 = -802,3;
= -802,3;  = 0;
= 0; = -283,0;
= -283,0;  = -241,8.
= -241,8.
 =
= 2KCl(к) + 3O2(г),
2KCl(к) + 3O2(г),




