
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Строение атомов, химическая связь и строение молекулСодержание книги
Поиск на нашем сайте
1. Квантово-механические представления о строении атомов. Характеристика энергетического состояния электрона системой квантовых чисел (главное квантовое и орбитальное).
Новые законы движения электронов и других микрочастиц были открыты в 1926 – 1928 гг. В.Гейзенбергом, Э.Шредингером, П.Дираком и др. Эти законы легли в основу одного из разделов современной физики - квантовой механики, которая описывает движение электронов и других частиц, обладающих очень малой массой – микрочастиц (электронов, фотонов, протонов, нейтронов и др.). Они резко отличаются от законов, определяющих движения больших тел – макрочастиц, к которым принадлежат предметы, видимые в оптический микроскоп или невооруженным глазом. Поэтому механику, применимую к движению обычных тел, основанную на законах Ньютона, стали называть классической механикой, а механика микрочастиц получила название квантовой механики (или волновой механики). Квант - неделимая порция какой-либо величины в физике; общее название определенных порций энергии (квант энергии), момента количества движения (углового момента), его проекции и других величин, которыми характеризуют физические свойства микро- (квантовых) систем. В основе современной теории строения атомов и молекул лежит представление квантовой механики о двойственной природе микрочастиц, то есть микротелам присуща корпускулярно-волновая двойственность, и микрочастицы могут проявлять себя как частицы и как волны. В отличие от теории Бора – Зоммерфельда квантовая механика не является искусственным соединением законов классическом механики с правилами квантования энергии. Это стройная теория, основанная на системе понятий, не содержащей противоречий. Все результаты, полученные на основе квантовой механики, находятся в полном соответствии с экспериментом.
Создание квантовой механики произошло в результате распространения представлений о двойственной природе фотонов света на все микрочастицы, в том числе на электроны. С одной стороны, свет представляет собой поперечные электромагнитные колебания волн, а с другой стороны свет состоит из материальных микрочастиц (фотонов), переносящих кванты энергии. Явления дифракции и интерференции света убедительно доказывают его волновую природу. В то же время свет обладает массой, энергией, давлением, вызывает фотоэффект (испускание электронов металлами при их освещении), то есть проявляет свойства частицы. Энергия фотона (кванта света) выражается уравнением Планка (1900г.): Е = h• ν, где h – постоянная Планка, равная 6,63•10-34 Дж•с, ν – частота колебания света, с-1. Но фотон света с энергией Е обладает и некоторой массой «m» в соответствии с уравнением А.Эйнштейна (1905 г.), которое справедливо как для макротел, так и для микрочастиц: Е = mc2, где с – скорость света, равная 3•108 м/с. Из двух последних уравнений следует, что hυ = mc2.
ν = с/λ, то получаем: h• После сокращений получаем соотношение
Таким образом, фотону света массой «m» и движущемуся со скоростью «с» соответствует волна длиной λ. В 1924 г. Луи де Бройль (Франция) предположил, что двойственная корпускулярно-волновая природа присуща не только фотонам света, но и всем микрочастицам, в том числе и электронам, то есть движение любой микрочастицы можно рассматривать как волновой процесс. Поэтому для электрона можно записать уравнение, аналогичное уравнению (9.1.) и называемое уравнением де Бройля:
Уравнение де Бройля (9.2.) устанавливает связь между корпускулярными и волновыми свойствами электрона. Согласно этому уравнению, электрону массой «m» и движущемуся со скоростью ν, соответствует волна длиной λ. Другими словами, каждая движущаяся микрочастица, в том числе и электрон, одновременно обладает свойствами волны. Гипотеза де Бройля о наличии у электрона волновых свойств была подтверждена экспериментально, когда в 1927 г. для электрона было установлено явление дифракции, причем длина волны электрона совпадала с рассчитанной по уравнению де Бройля (9.2.). Электрону с массой 9,1•10-31кг и скоростью порядка 106 м/с соответствует длина волны порядка 10-10 м, то есть длина волны электрона соизмерима с размерами атомов. Поэтому при рассеянии электронов кристаллами металлов наблюдается дифракция в результате взаимодействия пучка электронов с дифракционной решеткой, роль которой выполняют кристаллы металлов (то есть дифракция электронной волны наблюдается при взаимодействии электронов с атомами кристаллов). Если с помощью уравнения (9.2.) определить значения λ для макрочастиц, то для макрообъектов эти значения будут ничтожно малы. Так, для частицы массой 1 г и движущейся со скоростью 1 м/с длина волны λ = 6,63•10-31 м, что значительно меньше размеров атома и даже ядра атома (10-15 – 10-14 м), поэтому экспериментально волновой процесс обнаружить не удается.
Поскольку движение электрона имеет волновой характер, квантовая механика описывает его движение в атоме при помощи волновой функции ψ. Электрон в атоме может двигаться в любых направлениях. Поэтому электронная волна описывается волновой функцией от трех координат, то есть ψ = φ(x, y, z). В 1926 г. австрийский физик Э.Шредингер вывел уравнение, получившее название волнового уравнения Шредингера. Это основное уравнение квантовой механики, которое имеет такое же значение, как законы Ньютона для классической механики. Уравнение Шредингера является дифференциальным уравнением в частных производных:
Таким образом, волновое уравнение Шредингера связывает волновую функцию ψ с потенциальной энергией электрона U и его полной энергией Е и с пространственными координатами х, у, z. Волновая функция ψ в этом уравнении соответствует амплитуде волны, поэтому подобно амплитуде любого волнового процесса она может принимать как положительное, так и отрицательное значение. Важный физический смысл имеет квадрат волновой функции ψ2, который всегда положителен: произведение ψ2•∆V для электрона в атоме определяет вероятность нахождения электрона в малом объеме атома ∆V. Тогда величину ψ2 называют плотностью вероятности нахождения электрона в данной области атома или электронной плотностью. Решая уравнение Шредингера, можно для данного значения энергии электрона Е1 и заданных значений х, у, z рассчитать значение ψ, а затем и ψ2, то есть найти вероятность нахождения электрона в данном месте атомного пространства (или в данном объеме ∆V, если найти произведение ψ2•∆V). Рассчитывая значения ψ при других значениях энергии (Е2, Е3 и др.), можно описать движение электрона в атоме. Однако строгое точное решение уравнения Шредингера возможно только для одноэлектронных систем, например, для атома водорода. В более сложных системах применяют приближенные методы, которыми пользуется квантовая химия. Таким образом, решая уравнение Шредингера, можно получить энергетические уровни и волновые функции, которые описывают движение электронов в атоме. Волновую функцию φ(х, у, z), определяющую область наиболее вероятного нахождения электрона в атоме, называют атомной орбиталью. Атомные орбитали представляют собой математические волновые функции φ(х, у, z), по-разному зависящие от координат х, у, z. Такие функции удобно изображать графически в форме сферы, гантели и др. Эти изображения для кратности тоже называют атомными орбиталями. Но нужно помнить, что атомная орбиталь – это математическая волновая функция пространственных координат х, у, z. Представление о движении частицы в квантовой механике резко отличается от классической механики. Квантовая механика оперирует с вероятностями нахождения микрочастицы и ничего не говорит о траектории движения частицы, её координатах и скорости в тот или иной момент времени, так как эти понятия в квантовой механике не имеют смысла. Поэтому вместо выражения «движение электрона» в атоме (или молекуле) употребляют термин «состояние электрона» в атоме. В то же время в квантовой механике сохраняют свое значение понятия массы, энергии импульса микрочастицы.
Одним из основных положений квантовой механики, объясняющим корпускулярно-волновую двойственность микрочастиц, является принцип неопределенности, установленный в 1927 г. В.Гейзенбергом:
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 873; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 = mc2.
= mc2.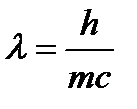 (9.1).
(9.1). (9.2.).
(9.2.). , (9.3)
, (9.3)


