
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Четырехполюсники. Классификация четырехполюсников. Уравнения четырехполюсников в форме H.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Четырёхполюсник — электрическая цепь с двумя парами зажимов, включенная таким образом, что через каждую пару зажимов проходят попарно равные и противоположно направленные токи (рис.). Четырехполюсники имеют важное практическое значение. При анализе электромагнитных процессов в большинстве электротехнических устройств (линиях, усилителях, трансформаторах и т.п.) эквивалентные схемы могут быть представлены в виде четырёхполюсников. Различают следующие виды четырёхполюсников: — линейные и нелинейные; линейные —4-полюсник, не содержащий нелинейных элементов нелинейный —4-полюсник, который содержит хотя бы 1 нелинейный элемент — пассивные и активные; активный —4-полюсник, содержащий источник энергии пассивный — 4-полюсник,не имеющий источников энергии --обратимый и необратимый обратимый —выполняется теорема обратимости(передаточные сопротивления не зависят от того, входная или выходная пара зажимов). В противном случае— необратимый -- симметричный (перемена мест входных и выходных зажимов не изменяет токов и напряжений), в противном случае— несимметричный -- уравновешенный (схема симметрична относительно продольной оси), неуравновешенный (1 из элементов может быть соединен с зажимом другой пары) — с сосредоточенными и распределенными элементами. Некоторые виды четырехполюсников независимо от их внутренней структуры обладают рядом общих свойств. Свойства четырехполюсника как системы передачи энергии определяются соотношениями между напряжениями на его внешних зажимах и токами, проходящими через эти зажимы. Уравнения передачи четырехполюсника — это уравнения, связывающие комплексные амплитуды напряжений и токов на двух парах зажимов четырехполюсника. При передаче электрических сигналов слева направо (прямое включение)зажимы 1−1′ являются входными, а зажимы 2 − 2′ — выходными. При обратном включении передача энергии происходит от зажимов2 − 2′, которые являются входными, к выходным зажимам1−1′ (рис. 2).
При этом токи на входе и выходе имеют комплексные значения I &1 и I &2, а напряжения – U &1 и U &2. (вместо & писать точку сверху)
Уравнения четырёхполюсника в форме А и в форме Y. Получить связь между первичными параметрами Y и А. Уравнения передачи четырехполюсника — это уравнения, связывающие комплексные амплитуды напряжений и токов на двух парах зажимов четырехполюсника. При передаче электрических сигналов слева направо (прямое включение)зажимы 1−1′ являются входными, а зажимы 2 − 2′ — выходными. При обратном включении передача энергии происходит от зажимов2 − 2′, которые являются входными, к выходным зажимам1−1′Существует 6 форм записи уравнений 4-хполюсника. А-форма:
параметры A 11 и A 22 являются безразмерными величинами,, A1 2 — имеет размерность сопротивления, а A 21 — проводимости. Y-форма:
Уравнения 4-хполюсников в форме А и в форме Z. Получить уравнения, связывающие первичные параметры А и Z. Уравнения передачи четырехполюсника — это уравнения, связывающие комплексные амплитуды напряжений и токов на двух парах зажимов четырехполюсника. При передаче электрических сигналов слева направо (прямое включение)зажимы 1−1′ являются входными, а зажимы 2 − 2′ — выходными. При обратном включении передача энергии происходит от зажимов2 − 2′, которые являются входными, к выходным зажимам1−1′Существует 6 форм записи уравнений 4-хполюсника.
параметры A 11 и A 22 являются безразмерными величинами,, A1 2 — имеет размерность сопротивления, а A 21 — проводимости. Для обратимых 4-хполюсников А12=А21 и тогда |А|=1, т.е. А11*А12 - А12*А21=1. При симметричном 4-хполюснике А11=А22. Z-форма:
Таким образом при параллельном регулярном соединении 4-хполюсников, матрица Y-параметров сложного 4-хполюсника равна сумме Y-параметров матриц соединённых 4-хполюсников.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 762; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.56 (0.012 с.) |




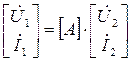

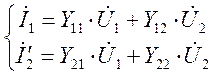 . Связь между первичными параметрами А и Y:
. Связь между первичными параметрами А и Y:  ,
,  ,
, 
 ,
,  . Для обратимых 4-хполюсников А12=А21 и тогда |А|=1, т.е. А11*А12 - А12*А21=1. При симметричном 4-хполюснике А11=А22.
. Для обратимых 4-хполюсников А12=А21 и тогда |А|=1, т.е. А11*А12 - А12*А21=1. При симметричном 4-хполюснике А11=А22.
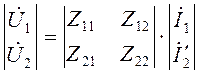 ,
,  . (
. ( ). Связь между первичными параметрами А и Z:
). Связь между первичными параметрами А и Z:  ,
,  ,
,  ,
,  .
. 75. Параллельно-параллельное соединение 4-хполюсников. Получить первичные параметры сложного четырёхполюсника.
75. Параллельно-параллельное соединение 4-хполюсников. Получить первичные параметры сложного четырёхполюсника. ,
,  .
.  ,
,  .
. ,
,  .
.  .
.  ,
,  .
.


