
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепи с распределенными параметрами. Первичные параметры однородной линии. Дифференциальные уравнения однородной линии.Содержание книги
Поиск на нашем сайте
После упрощения и деления уравнения на dx получим По первому закону Кирхгофа, Ток di (рис.2) равен сумме токов, проходящих через проводимость
Пренебрегаем слагаемыми второго порядка малости, тогда Подставим (3) в (2), упростим и поделим уравнение на dx: Уравнения (1) и (4) являются основными дифференциальными уравнениями для линии с распределенными параметрами.
51. Синусоидальный режим в однородной линии. Волновое сопротивление линии. Коэффициент распространения. Общий вид уравнений однородной линии. Обозначим комплексные действующие значения напряжения и тока на расстоянии x от начала линии через Применяя комплексную форму записи, получаем на основании уравнений Поскольку комплексные величины Исключая из системы (2) ток
Аналогично, исключая из системы (2) напряжение
Введём обозначение
и назовём эту величину коэффициентом распространения. Итак, уравнения (3) и (4) записываются в виде:
Получились однородные линейные дифференциальные уравнения второго порядка. Решение первого уравнения системы (6) имеет вид:
Ток
или
где
называется волновым сопротивлением линии. Подставим (5) в (7), получим:
Мгновенное значение напряжения в точке x равно мнимой части выражения
где
53. Синусоидальный режим в однородной линии. Обратная волна. Длина волны. Фазовая скорость.
Фазовая скорость обратной волны Итак, мгновенное напряжение можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причём каждая из этих волн затухает в направлении движения. На основании формул
т.е. за время, равное одному периоду, падающая и отражённая волны перемещаются на расстояние, равное длине волны.
54. Математическая модель длинной линии при синусоидальном воздействии. Коэффициенты отражения n1 и n2.
Линии, длина которых соизмерима с длиной волны, считаются длинными линиями. На высоких частотах практически любая протяжённая электрическая цепь становится «длинной» по отношению к длине волны. Возвращаясь к уравнениям где Напряжение и ток прямой и обратный волн связаны законом Ома: Это соотношение объясняет смысл термина «волновое сопротивление». Постоянные интегрирования A1 и A2, находятся в зависимости от напряжения и тока в начале линии при заданных граничных условиях. При x=0
откуда
Введём понятие коэффициента отражения волны в начале линии
где Подстановка A1 и A2 даёт:
Если заданы граничные условия на конце линии, то удобнее отсчитывать расстояние от конца, приняв координату
Получим окончательные результаты для U и I
Где аналогично предыдущему n2-коэфициент отражения в конце линии
Где
55. Вторичные параметры однородной линии. Зависимость коэффициентов a и b от частоты. Волновое сопротивление линии.
Вторичными линиями, или характеристическими, параметрами линии являются коэффициент ослабления, коэффициент фазы Из выражения Совместное решение этих уравнений дает
Из полученных выражений следует, что Полученные выражения неудобны для практического применения ввиду их громоздкости. Существует ряд приближенных расчетных формул для вычисления вторичных параметров линии, учытывающих, что в области высоких частот сопротивление Для уменьшения потерь при передаче электромагнитной энергии по линии стремятся к тому, чтобы сопротивление линии и проводимость изоляции были по возможности малы. Волновое сопротивление линии
При постоянном токе
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.01 с.) |

 -продольное активное сопротивление единицы длины линии;
-продольное активное сопротивление единицы длины линии; 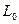 -индуктивность единицы длины линии;
-индуктивность единицы длины линии;  -емкость единицы длины линии;
-емкость единицы длины линии;  -поперечная проводимость единицы длины линии. Разобьем линию на участки длиной dx, где x-расстояние, отсчитываемое от начала линии. На длине dx активное сопротивление равно
-поперечная проводимость единицы длины линии. Разобьем линию на участки длиной dx, где x-расстояние, отсчитываемое от начала линии. На длине dx активное сопротивление равно  , индуктивность -
, индуктивность -  , проводимость утечки -
, проводимость утечки -  и емкость -
и емкость -  . Обозначим ток в начале рассматриваемого участка линии через i и напряжение между проводами линии в начале участка u. Если для некоторого момента времени t ток в начале рассматриваемого участка равен i, то в результате утечки через поперечный элемент ток в конце участка для того же момента времени равен
. Обозначим ток в начале рассматриваемого участка линии через i и напряжение между проводами линии в начале участка u. Если для некоторого момента времени t ток в начале рассматриваемого участка равен i, то в результате утечки через поперечный элемент ток в конце участка для того же момента времени равен  , где
, где  - скорость изменения тока в направлении x. Скорость, умноженная на расстояние dx, является приращением тока на пути dx. Аналогично, если напряжение в начале участка u, то в конце участка для того же момента времени напряжение равно
- скорость изменения тока в направлении x. Скорость, умноженная на расстояние dx, является приращением тока на пути dx. Аналогично, если напряжение в начале участка u, то в конце участка для того же момента времени напряжение равно 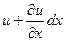 . Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной dx, обойдя его по часовой стрелке:
. Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной dx, обойдя его по часовой стрелке: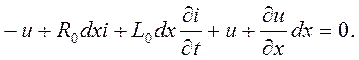
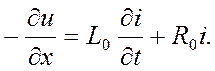 (1)
(1)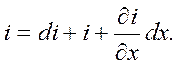 (2)
(2) :
: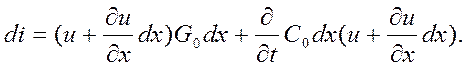
 (3)
(3)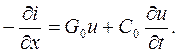 (4)
(4)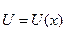 и
и 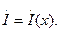
 (1) следующие уравнения
(1) следующие уравнения  (2).
(2). и
и  не зависят от t и являются функциями только x, при переходе от уравнений (1) к (2) частные производные по x заменены обыкновенными.
не зависят от t и являются функциями только x, при переходе от уравнений (1) к (2) частные производные по x заменены обыкновенными. (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)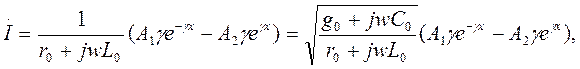
 (8)
(8)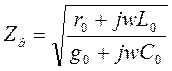 (9)
(9)

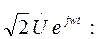
 (10)
(10)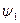 ,
,  - аргументы комплексных величин A1 и A2 соответственно.
- аргументы комплексных величин A1 и A2 соответственно. знак «-» указывает, что обратная волна движется в направлении, противоположном направлению прямой волны.
знак «-» указывает, что обратная волна движется в направлении, противоположном направлению прямой волны. и
и  запишем:
запишем: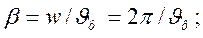

 и
и 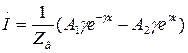 и записывая прямую и обратнуюволны в комплексной форме, имеем:
и записывая прямую и обратнуюволны в комплексной форме, имеем: 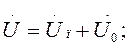


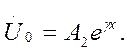






 - входное сопротивление линии.
- входное сопротивление линии.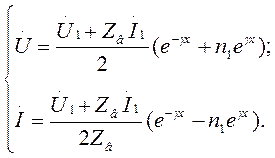
 Для A1 и A2 получаем следующие выражения:
Для A1 и A2 получаем следующие выражения:


 выходное сопротивление в конце линии.
выходное сопротивление в конце линии.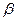 и волновое сопротивление
и волновое сопротивление  , которые выражаются через первичные параметры линии и частоту.
, которые выражаются через первичные параметры линии и частоту. следует, что
следует, что 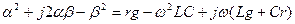 , откуда
, откуда  ;
;  .
.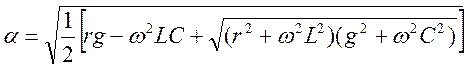

 и
и  весьма мало по сравнению с
весьма мало по сравнению с  , а проводимость
, а проводимость  ничтожна мала по сравнению с
ничтожна мала по сравнению с  .
.
 и бесконечной частоте
и бесконечной частоте  имеет действительные значения
имеет действительные значения и
и  В остальной части диапазона частот волновое сопротивление имеет емкостный характер, так как обычно
В остальной части диапазона частот волновое сопротивление имеет емкостный характер, так как обычно 



