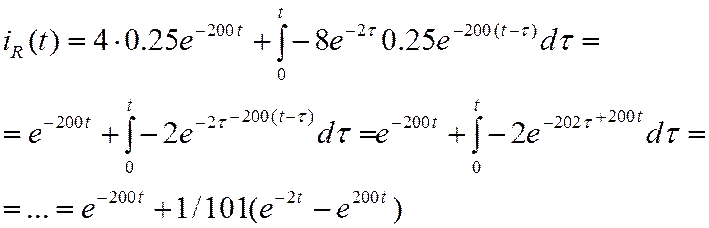Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения операторного метода расчетСодержание книги
Поиск на нашем сайте
переходных процессов. Прямое преобразование Лапласа. Основные положения опер. метода Т. к. дифер. уравнения пер. процессов в линейных цепях представляют собой лин. уравнения с постоянным коэф., то их можно интегр. операторным методом. сущонсть метода: заданная функцией(ф) вещественных переменной ф времени u(t), i(t) назыв. оригиналом сопостовления друг. ф. комплексн. переменной, которая наз. изображением. При этом производные интегралы от оригинала выражаются алгебр. ф. от изображения и начальных значений самой ф. её производных и интегралов. Поэтому система инт.-диф. уравнений заменяется системой алгебр. уравн. Полученная система уравнений решается. В результате определяем изображения искомых функций. При помощи обратных преобразований получаются оригиналы, т. е. искомые функции токов и напряжений от времени. Алгоритм: Оригиналы i(t), u(t)=>прямое преобразование Лапласа=>i(p) u(p)=>решение алгебраическ. Уравнений=>обратное пр-ние Лапласа=>искомые изображения=>графики i(t) u(t)
Прямое преобразование Лапласа. Пусть некоторая ф. f(t)=0 t<0 и имеет ограниченный рост при t>0 |f(t)|< M F(p) является ф. компл.-перемен, где p=jw и определена в полуплоскости Re[p]=S>=e f(t)=f(p)
20.Прямое преобразование Лапласа.Примеры получения изображений для элементарных функций Прямое преобразование Лапласа. Пусть некоторая ф f(t)=0 t<0 и имеет ограниченный рост при t>0 |f(t)|< Meft(ft-степень) действ., вещ. М1е числа то f(p)= F(p) является ф. компл.-перемен, где p=jw и определена в полуплоскости Re[p]=S>=e f(t)=f(p) Примеры получения изображений для элементарных ф-ий. f(t)={0, при t<0 и 1, при t>0 f(p)= f(t) =
21. Основные свойства преобразования Лапласа. Свойство линейности. Теорема дифференцирования. Предельные соотношения. Св-ва линейности Изображение лин. комбин. есть линейно комбин. изменение.
Теорема дифференцирования оригинала f `(t):=pF(p)-f(0)
1-ое предельное соотношение Lim(при t=>оо)f(t)=lim(при p=> oo)pF(p) 2-ое предельное соотношение Lim(при t=>оо)f(t)=lim(p=>0)pF(p) Они полезны для проверки преобразований Лапласа
22. Основные положения операторного метода расчета переходных процессов. Обратное преобразование Лапласа.
Основные положения опер. метода Т. к. дифер. уравнения пер. процессов в линейных цепях представляют собой лин. уравнения с постоянным коэф., то их можно интегр. операторным методом. сущонсть метода: заданная функцией(ф) вещественных переменной ф времени u(t), i(t) назыв. оригиналом сопостовления друг. ф. комплексн. переменной, которая наз. изображением. При этом производные интегралы от оригинала выражаются алгебр. ф. от изображения и начальных значений самой ф. её производных и интегралов. Поэтому система инт.-диф. уравнений заменяется системой алгебр. уравн. Полученная система уравнений решается. В результате определяем изображения искомых функций. При помощи обратных преобразований получаются оригиналы, т. е. искомые функции токов и напряжений от времени. Алгоритм: Оригиналы i(t), u(t)=>прямое преобразование Лапласа=>i(p) u(p)=>решение алгебраическ. Уравнений=>обратное пр-ние Лапласа=>искомые изображения=>графики i(t) u(t)
Обратное преобразование Лапласа Если функция F(p) аналитична и задана в полуплоскости Rep>c,при этом стремится к 0 при p=>oo, а также:
То f(t)=
23.Теорема разложения. Привести пример определения оригинала по заданному изображению. Теорема разложения f(p)=F1(p)\F2(p) =
f(p)=1\(p(p+a)(p+b)); p(p+a)(p+b)=0; p1=0; p2=-a; p3=-b; f2`(p)=(p^3+p^2a+p^2b+pab)`=3p^2+2ap+2bp+ab f(t)= I(p)=(0,86p+0,334)\(p^2+50p+10^5) F2(p)=p^2+50p+10^5=0=>p1,2=-25+-j315; F2`(p)=2p+50; I(t)=(0,286*(-25+j315)+33,4)e^p1t\2j315+(0,268(-25-j315)+33,4e^p2t)\-2j315=0,235e^-27tcos(35t-17,5);
1.ННУ 2.Операторная схема замещения 3.На основании схемы составить алгебраич. уравнен. 4.Решение этих ур-ий по отношению К неизвестному изобр. 5.по получ. изображениям определяем оригиналы 6. строим график
1.ННУ il(0-)=Е\(r1+r2); Uc(0-)=i2(0-)*r2;
2. 3.I2(p)=(E\p+iL(0-)*L)\(r2+pL); I3(p)=
I2(p)=(E\L)\(p*((r2\L)+p))+IL(0)\ ((r2\L)+p)
i2(t)= 25. Переходный процесс в RL-цепи при подключении к источнику постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
I(p)=E/r+pL=M(p)/N(p) Перходим от изображения к ее оригиналу i
F(p)=M(p)/N(p) r+pL=0 p=-r\L f(t)=E/L * e^(-rt/L)
26. Переходный процесс в RL-цепи при отключении источника постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
I(p)=L*i(0)/(r1+r2+pL)=M(p)/N(p) Перходим от изображения к ее оригиналу i F(p)=M(p)/N(p) r1+r2+pL=0 p=-(r1+r2)\L f(t)=E(r1+r2)/r1^2 * e^(-rt/L)
27. Переходный процесс в RL-цепи при подключении к источнику постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
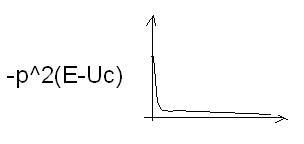
I(p)=E-Uc/(r+ 1/pC)=M(p)/N(p) Перходим от изображения к ее оригиналу i F(p)=M(p)/N(p) r+1/pC=0 p=-1/Cr f(t)=-p^2 (E-Uc)* e^(-t/C(r1+r2))
28. Переходный процесс в RC цепи при отключении источника постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
I(p)=Uc(0)/(r1+r2+1/pC)=M(p)/N(p) Перходим от изображения к ее оригиналу i F(p)=M(p)/N(p) r1+r2+1/pC=0 p=-1/C(r1+r2) f(t)=-p^2 E* e^(-t/C(r1+r2))
29. Переходные функции. Привести пример определения одной из переходных хар-к. Переходной характеристикой
Переходная проводимость – реакция электрической цепи, численно равной току при воздействии на эту цепь единичной ступенчатой функции напряжения.
Переходная функция напряжения - это реакция электрической цепи, численно равная напряжению при воздействии на эту цепь единичной ступенчатой функции напряжения.
Переходная функция тока - реакция цепи, численно равной току при воздействии на эту цепь единичной функции тока.
Переходное сопротивление – реакция электрической цепи в виде напряжения при воздействии единичной ступенчатой функции тока.
Каким бы не было заданное входное воздействие или ток источников, его принимают равным 1В или 1А. 1) Определяют ННУ Пример. Найти переходную характеристику по току для цепи для ветви с сопротивлением
Решение 1) 2) ННУ 3) 4) 5)
6) ЗНУ
7) Полное решение 8) Переходное характеристика безразмерна:
30.Интеграл Дюамеля.
При достаточно малом Следовательно, для рассматриваемого момента времени
При
31. Расчет переходных процессов методом интеграла Дюамеля. Рассмотреть на примере.
На входе непериодические несинусоидальные сигналы
Общая формула интеграла Дюамеля:
Для нашего случая
Переходная проводимость g(t) есть реакция цепи на единичное ступенчатое воздействие.
Подадим на вход единичное напряжение, на выходе получим единичный ток:
Схема:
Ток Ir(t) будет равен проводимости переходной характеристики.
Найдём этот ток. 1.ННУ: 2. Установившийся режим: 3. Свободный режим:
4.ЗНУ:
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.131 (0.012 с.) |

 действ., вещ. М1е числа то f(p)=
действ., вещ. М1е числа то f(p)=  f(t)
f(t)  dt и этот интеграл абсолютно сходится
dt и этот интеграл абсолютно сходится 1
1  f(p)=
f(p)=  dt=
dt=  |0 =
|0 =  ;
; 

 сходится абсолютно
сходится абсолютно
 f(p):=f(t)
f(p):=f(t)
 =1\ab+
=1\ab+  +
+  ;
; 24.Алгоритм расчета переходного процесса операторным методом. Рассмотреть на примере r, L, c – цепи.
24.Алгоритм расчета переходного процесса операторным методом. Рассмотреть на примере r, L, c – цепи.
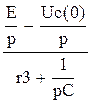 =
= 
 +IL(0-)*
+IL(0-)* 



 (p) при помощи формулы разложения
(p) при помощи формулы разложения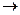 f(t)=
f(t)=  e^p
e^p  t, p
t, p 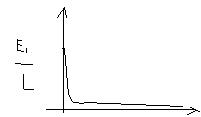








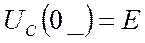


 называется уравнение, составленное для участка цепи или для всей в це
называется уравнение, составленное для участка цепи или для всей в це  лом, которое описывает переходный процесс, если цепь подсоединяется к источнику с постоянным входным сигналом равным 1 (1А или 1В).
лом, которое описывает переходный процесс, если цепь подсоединяется к источнику с постоянным входным сигналом равным 1 (1А или 1В). – переходная характеристика для тока
– переходная характеристика для тока – переходная
– переходная  – переходное сопротивление
– переходное сопротивление – переходная проводимость
– переходная проводимость


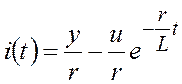 , т.к
, т.к  , то
, то  , (1)
, (1) , (2)
, (2)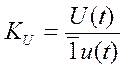

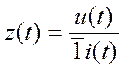
 и
и  и т.д. т.е. для полученной цепи рассчитываем п/пр. любым методом. Полученные уравнения для
и т.д. т.е. для полученной цепи рассчитываем п/пр. любым методом. Полученные уравнения для  и
и  дадут соответствующие переходные характеристики.
дадут соответствующие переходные характеристики. при воздействии на входе ИТ
при воздействии на входе ИТ 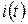


 ,
,  .
.


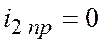

 , где
, где  ,
,  ,
,  .
.
 наедем из после коммутационной схемы:
наедем из после коммутационной схемы:

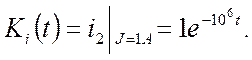

 – все время действия функции. Этот разбиваем на элементарные скачки и заменяем приближенной ступенчатой функцией.
– все время действия функции. Этот разбиваем на элементарные скачки и заменяем приближенной ступенчатой функцией.
 реакция цепи на первый прямоугольный импульс приближенно равна реакции цепи на единичную функцию помноженную на высоту первой ступени:
реакция цепи на первый прямоугольный импульс приближенно равна реакции цепи на единичную функцию помноженную на высоту первой ступени:  . Реакция цепи на вторую ступень:
. Реакция цепи на вторую ступень: 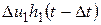 , где
, где 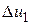 - высота второй ступени;
- высота второй ступени;  - реакция цепи на единичную функцию, смещенную в сторону запаздывания на
- реакция цепи на единичную функцию, смещенную в сторону запаздывания на 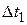 и т.д.
и т.д. реакция цепи
реакция цепи  равна:
равна:
 и
и 
 -это первая форма записи интеграла Дюамеля, т.е. выходной сигнал:
-это первая форма записи интеграла Дюамеля, т.е. выходной сигнал:


 R=2 Ом L=5 мГн
R=2 Ом L=5 мГн
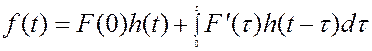




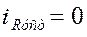 .
.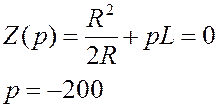


 в итоге получаем ток:
в итоге получаем ток: