
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классический метод анализа переходных процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Начальные условия
Значения напряжений на емкостях и токов в индуктивностях цепи в момент коммутации, т. е. в начальный момент, образуют независимые начальные условия задачи. Независимые начальные условия определяют начальный запас энергии в цепи. Различают задачи с нулевыми начальными условиями, когда для всех емкостей uC(0+) = 0 и для всех индуктивностей iL(0+) = 0, и с ненулевыми, когда указанные требования нарушаются хотя бы в одном из реактивных элементов. Независимые начальные условия могут быть заданы или рассчитаны с применением законов коммутации. Начальные значения токов в ветвях без катушек индуктивности или напряжений на элементах, не являющихся конденсаторами, называются зависимыми начальными условиями. Они определяются по независимым начальным условиям с применением законов Кирхгофа или других методов расчета для момента времени t = 0+.
Переходный процесс в r, L – цепи при включении на источник постоянного напряжения
1. iL(0-)=0 2. iуст=E/r 3. a)ri+Ldi/dt=E b)z(jw)=r+jwL Lp+r=0 jw p=-r/L z(p)=0 0=pL+r iLсв(t)=Aept 4. iL(t)=iуст+iсв(t)=E/r+Aept iL(0)=E/r+A 0=E/r+A 5. iL(t)=E/r(1-e-rt/r)
Отключение r-l цепи от источника пост напряж
1. iL(0-)=E/r1 2. iLуст=0 3. z(jw)=r1+r2 +jwL z(jw)=z(p) r1+r2+ph=0 4. 4. iL(t)=iLуст + Aept iL(0)=AE/r1 iL(t)=E/r1*e-(r1+r2)/2 Ur(0)=-I(r1+r2)=-E(r1+r2)/r1 UL(t)=-[E(r1+r2)/r1]*e-(r1+r2)t/L
Включение r-L цепи на синусоидальном токе
1. iL(0-)=0 2. iLуст(t)=e(t)=Emsin(wt+ Imaxуст=Em/√(r2+XL2) iLmaxуст(t)=Imaxsin(wt+ iLуст(0)=Imaxуст*sin( 3. p=-r/L 4. iL(t)=iуст(t)+iLсв(t) iL(t)=Imaxsin(wt+ t=0: iL(0)=iLуст(0)+A 0=Imaxустsin( A=-Imaxустsin( iL(t)=Imaxуст*sin(wt+
Алгоритм расчета переходных процессов классическим методом. Пример расчета. В классическом Число уравнений в этом случае равно числу ветвей схемы методе находится решение в виде суммы общего и частного решения. Расчета переходный процесс описывается системой обыкновенных дифф.уравнений, составленных одним из методов расчета для мгновенных значений функций времени. Решение для каждой переменной этой системы находится в виде суммы общего и частного решения. Для составления уравнения могут быть использованы: метод, основанный на применении законов Кирхгофа, метод узловых потенциалов, метод контурных токов и т.д. Например, система дифференциальных уравнений, составленная после коммутации согласно первому и второму законам Кирхгофа, имеет вид:
Например, Число уравнений в этом случае равно числу ветвей схемы. Пусть требуется найти ток ik в ветви с номером К.Исключая последовательно токи ветвей, в результате получим ток ik и его производные до порядка n:
Порядок дифф.уравнения n определяется количеством независимых реактивных элементов схемы (m). Обычно n=m, но в зависимости от способа соединения может быть и так, что n<m. Это будет, например, в случаях, когда индуктивные и емкостные элементы включены последовательно, или, например, когда емкости соеденениы парал. И имеют одинаковые нач условия(рис9,4):
Последовательно включенные емкостные элементы можно заменить одним элементом, так же как и парал включенные индуктивные элементы можно заменить одним эквивалентным. На рисунке 9.5 показана замена 2х последовательно включенных емкостей одной эквивалентной.
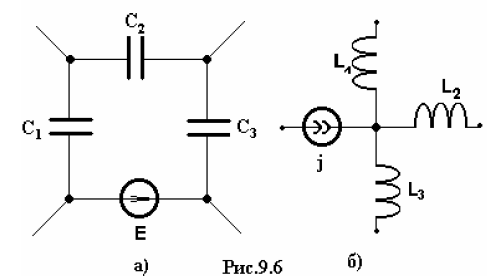
В общем случае порядок диф.уравнения n равен: n=nlc-nce-nlj, где nlc-количество реактивных элементов(L и C) в схеме, nce- количество емкостных контуров, nlj-количество индуктивных узлов или сечений. Под ёмкостным понимается контур, состоящих из емкостных элементов или емкостных элементов и идеальных источников ЭДС, рис 9.6.а.Под индуктивным понимается узел, в который сходятся индуктивные ветви или индуктивные ветви и источники тока(рис. 9.6.б), либо сечения, которые пересекают только индуктивные ветви или индуктивные ветви и источники тока.
Отметим, что этап составления диф.уравнения не явл-ся обязательным и переходный ток или напряжение могут быть найдены без составления ур-ния. Как было указано, в классическом методе расчета переходных процессов решения уравнений Частное решение описывает режим, который называется принужденным. Решение однородного уравнения(правая часть равна нулю) описывает процесс при отсутствии внешних ЭДС и источников тока и называется свободным. Соответственно рассматриваются свободные и принужденные токи, напряжения, заряды. Таким образом, ток в ветви с номером К представляется в виде суммы
Теорема разложения f(p)=F1(p)\F2(p) =
f(p)=1\(p(p+a)(p+b)); p(p+a)(p+b)=0; p1=0; p2=-a; p3=-b; f2`(p)=(p^3+p^2a+p^2b+pab)`=3p^2+2ap+2bp+ab f(t)= I(p)=(0,86p+0,334)\(p^2+50p+10^5) F2(p)=p^2+50p+10^5=0=>p1,2=-25+-j315; F2`(p)=2p+50; I(t)=(0,286*(-25+j315)+33,4)e^p1t\2j315+(0,268(-25-j315)+33,4e^p2t)\-2j315=0,235e^-27tcos(35t-17,5);
1.ННУ 2.Операторная схема замещения 3.На основании схемы составить алгебраич. уравнен. 4.Решение этих ур-ий по отношению К неизвестному изобр. 5.по получ. изображениям определяем оригиналы 6. строим график
1.ННУ il(0-)=Е\(r1+r2); Uc(0-)=i2(0-)*r2;
2. 3.I2(p)=(E\p+iL(0-)*L)\(r2+pL); I3(p)=
I2(p)=(E\L)\(p*((r2\L)+p))+IL(0)\ ((r2\L)+p)
i2(t)= 25. Переходный процесс в RL-цепи при подключении к источнику постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
I(p)=E/r+pL=M(p)/N(p) Перходим от изображения к ее оригиналу i F(p)=M(p)/N(p) r+pL=0 p=-r\L f(t)=E/L * e^(-rt/L)
26. Переходный процесс в RL-цепи при отключении источника постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
I(p)=L*i(0)/(r1+r2+pL)=M(p)/N(p) Перходим от изображения к ее оригиналу i F(p)=M(p)/N(p) r1+r2+pL=0 p=-(r1+r2)\L f(t)=E(r1+r2)/r1^2 * e^(-rt/L)
27. Переходный процесс в RL-цепи при подключении к источнику постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
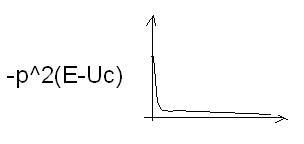
I(p)=E-Uc/(r+ 1/pC)=M(p)/N(p) Перходим от изображения к ее оригиналу i F(p)=M(p)/N(p) r+1/pC=0 p=-1/Cr f(t)=-p^2 (E-Uc)* e^(-t/C(r1+r2))
28. Переходный процесс в RC цепи при отключении источника постоянного напряжения(операторный метод).
iL(t), UL(t); 1.Независимые начальные условия 2. Составляем операторную схему замещения.
I(p)=Uc(0)/(r1+r2+1/pC)=M(p)/N(p) Перходим от изображения к ее оригиналу i F(p)=M(p)/N(p) r1+r2+1/pC=0 p=-1/C(r1+r2) f(t)=-p^2 E* e^(-t/C(r1+r2))
29. Переходные функции. Привести пример определения одной из переходных хар-к. Переходной характеристикой
Переходная проводимость – реакция электрической цепи, численно равной току при воздействии на эту цепь единичной ступенчатой функции напряжения.
Переходная функция напряжения - это реакция электрической цепи, численно равная напряжению при воздействии на эту цепь единичной ступенчатой функции напряжения.
Переходная функция тока - реакция цепи, численно равной току при воздействии на эту цепь единичной функции тока.
Переходное сопротивление – реакция электрической цепи в виде напряжения при воздействии единичной ступенчатой функции тока.
Каким бы не было заданное входное воздействие или ток источников, его принимают равным 1В или 1А. 1) Определяют ННУ Пример. Найти переходную характеристику по току для цепи для ветви с сопротивлением
Решение 1) 2) ННУ 3) 4) 5)
6) ЗНУ
7) Полное решение 8) Переходное характеристика безразмерна:
30.Интеграл Дюамеля.
При достаточно малом Следовательно, для рассматриваемого момента времени
При
31. Расчет переходных процессов методом интеграла Дюамеля. Рассмотреть на примере.
На входе непериодические несинусоидальные сигналы
Общая формула интеграла Дюамеля:
Для нашего случая
Переходная проводимость g(t) есть реакция цепи на единичное ступенчатое воздействие.
Подадим на вход единичное напряжение, на выходе получим единичный ток:
Схема:
Ток Ir(t) будет равен проводимости переходной характеристики.
Найдём этот ток. 1.ННУ: 2. Установившийся режим: 3. Свободный режим:
4.ЗНУ:
Z1/2 Z1/2
Звено
Поскольку фильтры будут симметричными то из Г-образного звена можно получить П-образное и Т образное звено.
Z1/2 Z1/2 Z1
2. Четырёхполюсник обретает свойства фильтра только в том случае если сопротивления Z1 и Z2 имеют разные знаки
3. Четырёхполюсник симметричный (
Это соотношение справедливо как для T так и для П схемы.
4.
↓U1 Z2 U2↓ (1)
(2)
Ф-лы описывают математически полосу пропускания и задерживания и фазу фильтра.
5.1 Полоса пропускания а=0 5.2 Полоса задерживания
ФНЧ
Загрождающий.
Недостатки: сущ затухание в полосе пропускания
49. Безындуктивные фильтры на RC – элементах. Основные характеристики, электрические схемы полосового и полосно-заграждающего фильтров.
r/2
C/2
0 fc f
C/2 ФВЧ-фильтр
2R a
0 fc f
Полосовой фильтр
0 fc1 fm fc2 f
Заграждающий фильтр
R2 R2
C1 C1 R1 C2
0 fc1 fm fc2 f
P.S.1
Tgg= P.S.2 Chg= Симметричный 4-хполюсник.
1Б= затухание сигнала по мощности в 10 раз. 1Б=lg
1Дб=20lg10.
Замечание а) зависимым источником являются необратимым элементом с односторонним перед. сигнала только в прямом направлении. б) зависимый источник не потребляет энергию, а генерируют её, т.е. могут снабжать энергией цепь, которая присоед. к вых. Элем, которые могут усиливать сигналы, поступ. на вход – активные значения завис. источн. является резистивными активными 4-х полюсными элементами. В)при математическом описании ур-е завис. ист. содержит только по одному параметру
ИНУН ИНУТ
Начальные условия
Значения напряжений на емкостях и токов в индуктивностях цепи в момент коммутации, т. е. в начальный момент, образуют независимые начальные условия задачи. Независимые начальные условия определяют начальный запас энергии в цепи. Различают задачи с нулевыми начальными условиями, когда для всех емкостей uC(0+) = 0 и для всех индуктивностей iL(0+) = 0, и с ненулевыми, когда указанные требования нарушаются хотя бы в одном из реактивных элементов. Независимые начальные условия могут быть заданы или рассчитаны с применением законов коммутации. Начальные значения токов в ветвях без катушек индуктивности или напряжений на элементах, не являющихся конденсаторами, называются зависимыми начальными условиями. Они определяются по независимым начальным условиям с применением законов Кирхгофа или других методов расчета для момента времени t = 0+.
Классический метод анализа переходных процессов
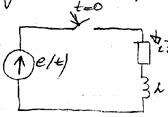
Классический метод анализа переходных процессов основан на составлении системы дифференциальных и алгебраических уравнений с использованием уравнений для элементов и законов Кирхгофа для мгновенных токов и напряжений в цепи:
Для определения интересующей реакции систему исходных уравнений путем исключения остальных переменных приводят к одному линейному уравнению n-го порядка с постоянными коэффициентами:
где i(t) - искомая переменная; f(t) - правая часть, обусловленная возмущающими силами, т.е. функциями источников. Напомним известные из курса математики сведения о решении линейных дифференциальных уравнений. Общее решение линейного дифференциального уравнения (1.4) определяется в виде суммы двух составляющих: i(t) = iсв(t) + iвын(t). (1.5) Первая составляющая называется свободной или собственной и определяется как общее решение соответствующего однородного уравнения, которое получается из (1.4) путем приравнивания нулю правой части f(t) = 0:
Для определения общего решения (1.6) составляется характеристическое уравнение, которое получается из (1.6) путем замены k -той производной на pk. При этом сама искомая переменная заменяется на единицу. Характеристическое уравнение
pn + bn-1pn-1 +........... +b1p + b0 = 0(1.7) является алгебраическим уравнением степени n и его корни pk определяют общее решение однородного дифференциального уравнения:
где Ak - постоянные интегрирования.
Решение (1.8) записано для случая различных корней pk. Входящие в (1.8) n постоянных интегрирования определяются по известным независимым начальным условиям.
Заметим, что в однородном дифференциальном уравнении (1.6) правая часть приравнивается нулю, что означает отсутствие в цепи внешнего воздействия, т.е. источника. Поэтому токи и напряжения в ветвях цепи будут определяться только параметрами и свойствами самой цепи, а также начальным запасом энергии. Физически очевидно, что для реальных цепей собственная составляющая iсв(t) при отсутствии источников должна стремиться со временем к нулю. Эта составляющая существует во время переходного процесса.
Вторая составляющая iвын(t) решения (1.5) называется вынужденной и представляет собой частное решение неоднородного дифференциального уравнения (1.4) (с ненулевой правой частью). Из математики известно, что вид частного решения определяется видом правой части уравнения. В частности, если правая часть f(t) - константа, то и частное решение ищется в виде константы. Если правая часть является гармонической функцией с определенными частотой, амплитудой и начальной фазой, то и частное решение будет гармонической функцией той же частоты, для которой нужно определить амплитуду и начальную фазу.
Таким образом, вынужденная составляющая обусловлена воздействием источников в цепи и при t ®Ґ искомая переменная i(t) ® iвын(t). Поэтому вынужденная составляющая называется установившейся и определяется как установившееся значение (в случае постоянной вынуждающей силы) или как установившаяся функция (в случае гармонической вынуждающей силы) для искомой переменной в цепи после коммутации iвын(t) = iуст(t) (1.9) Необходимо отметить, что определение вынужденной составляющей в случае воздействия сигналов более сложной формы, чем упомянутые выше, представляет достаточно сложную задачу. В заключении приведем рекомендуемый порядок расчета переходных процессов классическим методом. 1. Определить независимые начальные условия iLk(0+) и uCk(0+) с использованием законов коммутации. 2. Для цепи после коммутации составить систему уравнений Кирхгофа с использованием уравнений для элементов. 3. Полученную систему разрешить относительно искомой переменной. При этом получится одно дифференциальное уравнение n-ой степени, где n равно общему числу индуктивностей и емкостей, в которых можно задавать независимые начальные условия. 4. Определить решение полученного дифференциального уравнения
где iвын(t)=iуст(t) -вынужденная (установившаяся) составляющая; pk - корни характеристического уравнения; Ak - постоянные интегрирования, определяемые из начальных условий.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.163 (0.009 с.) |


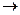 p
p p=-r/L
p=-r/L


 )
) -
- 

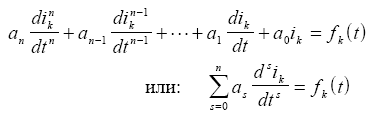


 представляется виде суммы общего и частного решения.
представляется виде суммы общего и частного решения. .
.
 =1\ab+
=1\ab+  +
+  ;
; 24.Алгоритм расчета переходного процесса операторным методом. Рассмотреть на примере r, L, c – цепи.
24.Алгоритм расчета переходного процесса операторным методом. Рассмотреть на примере r, L, c – цепи.
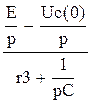 =
= 
 +IL(0-)*
+IL(0-)* 



 (p) при помощи формулы разложения
(p) при помощи формулы разложения e^p
e^p  t, p
t, p 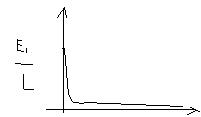








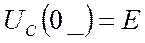


 называется уравнение, составленное для участка цепи или для всей в це
называется уравнение, составленное для участка цепи или для всей в це  лом, которое описывает переходный процесс, если цепь подсоединяется к источнику с постоянным входным сигналом равным 1 (1А или 1В).
лом, которое описывает переходный процесс, если цепь подсоединяется к источнику с постоянным входным сигналом равным 1 (1А или 1В). – переходная характеристика для тока
– переходная характеристика для тока – переходная
– переходная 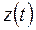 – переходное сопротивление
– переходное сопротивление – переходная проводимость
– переходная проводимость


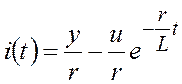 , т.к
, т.к 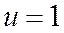 , то
, то  , (1)
, (1) , (2)
, (2)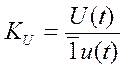

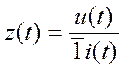
 и
и  и т.д. т.е. для полученной цепи рассчитываем п/пр. любым методом. Полученные уравнения для
и т.д. т.е. для полученной цепи рассчитываем п/пр. любым методом. Полученные уравнения для  и
и  дадут соответствующие переходные характеристики.
дадут соответствующие переходные характеристики. при воздействии на входе ИТ
при воздействии на входе ИТ 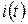


 ,
,  .
.


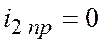

 , где
, где  ,
,  ,
,  .
.
 наедем из после коммутационной схемы:
наедем из после коммутационной схемы:

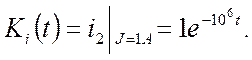

 – все время действия функции. Этот разбиваем на элементарные скачки и заменяем приближенной ступенчатой функцией.
– все время действия функции. Этот разбиваем на элементарные скачки и заменяем приближенной ступенчатой функцией.
 реакция цепи на первый прямоугольный импульс приближенно равна реакции цепи на единичную функцию помноженную на высоту первой ступени:
реакция цепи на первый прямоугольный импульс приближенно равна реакции цепи на единичную функцию помноженную на высоту первой ступени:  . Реакция цепи на вторую ступень:
. Реакция цепи на вторую ступень: 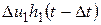 , где
, где 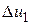 - высота второй ступени;
- высота второй ступени;  - реакция цепи на единичную функцию, смещенную в сторону запаздывания на
- реакция цепи на единичную функцию, смещенную в сторону запаздывания на 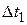 и т.д.
и т.д. реакция цепи
реакция цепи  равна:
равна:
 и
и 
 -это первая форма записи интеграла Дюамеля, т.е. выходной сигнал:
-это первая форма записи интеграла Дюамеля, т.е. выходной сигнал:


 R=2 Ом L=5 мГн
R=2 Ом L=5 мГн
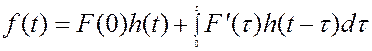




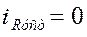 .
.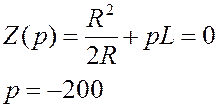


 в итоге получаем ток:
в итоге получаем ток: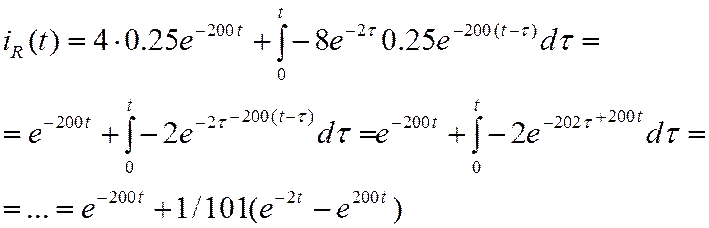

 → 2Z2 ←
→ 2Z2 ←  Г- образное
Г- образное Z1/2 Z1/2 Z1/2 Z1/2
Z1/2 Z1/2 Z1/2 Z1/2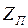 →
→

 )
)
 Для Г-образного звена
Для Г-образного звена 
 Z1/2
Z1/2



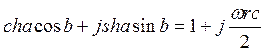




 ФВЧ
ФВЧ
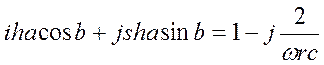


 Полосовой фильтр.
Полосовой фильтр.



 a
a









 R1 c2
R1 c2  а
а

 а
а



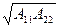 Shg=
Shg= 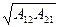














 ИТУТ
ИТУТ 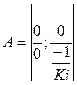
 ИТУН
ИТУН 


 ,(1.4)
,(1.4) (1.6)
(1.6)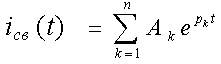 , (1.8)
, (1.8) (1.10)
(1.10)


