
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическое программирование. Марковские процессы принятия решений (динамические модели стохастических процессов принятия решений).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть некоторая система в любой фиксированный момент t может находиться в одном из n состояний и перейти из этого состояния в любое другое. Пусть вероятность Pt(i,j) перехода в момент t из i-го состояния в j-е не зависит от предыстории системы. Такая система называется Марковской. Рассматриваются многошаговые процессы принятия решений, такие, что состояния на каждом шаге являются случайными. Система с конечным, либо бесконечным горизонтом планирования. Переход из некоторого состояния на некотором шаге в другое возможное состояние описывается соответствующей переходной вероятностью. Переход их некоторого состояния во все возможные описывается стохастическим вектором, а все возможные переходы – матрицей переходных вероятностей. Каждый конкретный переход приводит к некоторому результату. Возможности управления сводятся к выбору соответствующих матриц переходных вероятностей. Каждой матрице переходных вероятностей сопоставляется соответствующая матрица результатов (доходов или потерь). Необходимо выбирать такие управления на шагах, чтобы ожидаемый (средний) доход, получаемый на конечном или бесконечном плановом периоде, был оптимальным. Мы будем рассматривать задачу с конечным плановым периодом. Задача о садовнике. Некто берет в аренду земельный участок на n лет и собирается использовать его для выращивания сельскохозяйственных культур. Состояние почвы может быть хорошим (Х), удовлетворительным (У) и плохим (П). Состояние почвы может меняться. Нужно принимать решения о внесении удобрений. Изменение состояния почвы при решении не вносить удобрения описывается следующей матрицей.
Буквы х у п по вертикали означают состояние почвы в начале года, по горизонтали – в конце года. Соответствующий элемент матрицы – вероятность того, что если не вносить удобрения состояние почвы изменится таким образом. Например, вероятность того, что без внесения удобрений почва из хорошей в начале года станет удовлетворительной в конце года равна 0.4. Соответствующая матрица дохода с учетом решения:
Аналогичными матрицами описывается состояние почвы и дохода при решении вносить удобрения:
Рассмотрим теперь общий подход к решению подобных задач. Имеем систему Переходы между состояния описываются матрицами вероятностей переходов в зависимости от управления: вероятность того, что при управлении Нарисуем схему данной задачи:
Рассмотрим последний шаг. При переходе по дуге 4 выигрыш равен
эту величину и будем рассматривать в качестве дохода. Рассмотрим произвольный
Решим задачу методом динамического программирования: Обратная прогонка: N-й шаг:
………………………………………………………………………….. n-й шаг:
………………………………………………………………………….. 1-й шаг:
Состояние на 1-м шаге может быть определено, а может быть только дана вероятность состояний на 1-м шаге. Во втором случае следует взвесить Возможности усложнения: · матрицы переходов состояний и доходов меняются в зависимости от шага: · учитывается влияние инфляции: ·
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 989; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

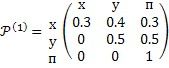


 с множеством состояний
с множеством состояний  и множество управлений
и множество управлений  будем описывать их просто индексами
будем описывать их просто индексами  . Рассматривается управление системой на
. Рассматривается управление системой на  шагах (шаги:
шагах (шаги:  ).
). система перейдет из состояния
система перейдет из состояния  в состояние
в состояние  :
:  – соответствующий элемент матрицы
– соответствующий элемент матрицы  . Доходы при соответствующих переходах в зависимости от управления описываются матрицами доходов в зависимости от управления: доход от перехода системы из состояния
. Доходы при соответствующих переходах в зависимости от управления описываются матрицами доходов в зависимости от управления: доход от перехода системы из состояния  – соответствующий элемент матрицы
– соответствующий элемент матрицы  .
.
 и зависит от управления. При переходе по дуге 5:
и зависит от управления. При переходе по дуге 5:  , по дуге 6:
, по дуге 6:  . Располагая только информацией, что в начале
. Располагая только информацией, что в начале  – м состоянии, и мы знаем, с какой вероятностью можем попасть, в результате шага, в любое другое состояние, взвесим полученные возможные доходы от применяемого управления по вероятности:
– м состоянии, и мы знаем, с какой вероятностью можем попасть, в результате шага, в любое другое состояние, взвесим полученные возможные доходы от применяемого управления по вероятности:
 - й шаг. При переходе по дуге 1 выигрыш равен
- й шаг. При переходе по дуге 1 выигрыш равен  и зависит от управления. При переходе по дуге 2:
и зависит от управления. При переходе по дуге 2:  , по дуге 3:
, по дуге 3:  . Как и в случае последнего шага, эти выигрыши стоит взвесить по вероятности, чтобы найти математическое ожидание выигрыша (средний выигрыш) при применении выбранного управления:
. Как и в случае последнего шага, эти выигрыши стоит взвесить по вероятности, чтобы найти математическое ожидание выигрыша (средний выигрыш) при применении выбранного управления: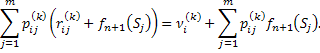
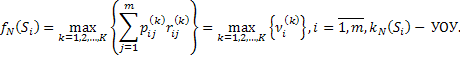



 по вероятностям
по вероятностям  и в качестве начального состояния взять такое, для которого значение
и в качестве начального состояния взять такое, для которого значение  является наибольшим.
является наибольшим. ;
; – коэффициент инфляции,
– коэффициент инфляции,  – коэффициент дисконтирования, тогда:
– коэффициент дисконтирования, тогда:  ;
; , при бесконечном плановом периоде нужно ориентироваться на средние доходы по каким-то интервалам.
, при бесконечном плановом периоде нужно ориентироваться на средние доходы по каким-то интервалам.


