
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многокритериальная оптимизация, метод равенства.Содержание книги
Поиск на нашем сайте
Если локальные критерии нормированы и равнозначны, то естественным может быть стремление к поиску решения, обеспечивающего равные и максимально возможные эффективности по всем локальным критериям.
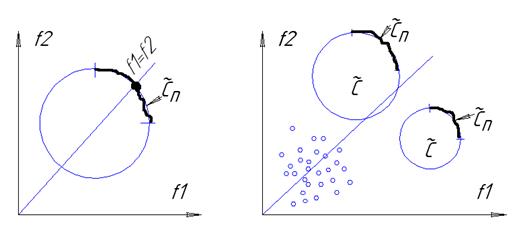
Метод квазиравенста
Многокритериальная оптимизация maxmin подход.
2) последовательный maxmin
Такие стратегии из
Стратегии из Локальные оценки должны быть нормированы.
Многокритериальная оптимизация, проблемы, классы задач Типы задач: ВОЗ (векторные оптимальные задачи) на множестве целей или качеств Рассматриваются системы или объекты, любые из которых характеризуются некоторым набором качеств. В общем случае качества могут быть противоречивыми и несовместными. Необходимо брать такую систему, которая в «некотором смысле» будет наилучшей В таких задачах обычно локальные оценки неоднородны – [кг], [руб], [км] Пример: автомобиль Оценки: стоимость, динамические характеристики, топливная эффективность, надежность, комфортность, тип Эти качества противоречивы и иногда несовместны, но проблема выбора существует. ВОЗ на множестве объектов Рассматриваемая система состоит из различных объектов или подсистем. Эффективность функционирования любого объекта оценивается скалярным критерием, системы – глобальным (векторным) критерием
Вопрос распределения инвестиций Как правило, в таких задачах критерии являются однородными. ВОЗ на множестве условий В таких постановках рассматриваемая система может находиться в различных условиях эксплуатации. Для любого конкретного условия качество системы характеризуется скалярным критерием. Для любых возможных условий качество характеризуется векторным критерием. Необходимо найти такие решения, которые окажутся наилучшими для любых условий эксплуатации. Локальные оценки обычно однородны. ВОЗ на множестве этапов Рассматриваемая система в своем эксплутационном цикле проходит через различные этапы. На любом этапе эффект системы оценивается скалярным критерием, на множестве этапов – векторным. Необходимо найти решение для всего жизненного цикла системы.
Локальные оценки однородны.
Примеры:
Самолет:
ВОЗ на множестве постановок В таких заданиях есть неопределенность различных постановок задачи направленных на увеличение эффективности системы. Эффективность любой постановки характеризуется локальным критерием, эффективность системы в целом – глобальным критерием. Необходимо найти сочетание постановок, которое окажется наиболее эффективным для систем в целом. Пример:
(задачи в условиях неопределенности пересекаются с этим ВОЗ) ВОЗ «вложенные» (многовекторные) Каждый локальный критерий, характеризующий качество, объект, условие или этап в свою очередь являются векторным Множество стратегий
Найти Проблемы:
Многокритериальная оптимизация, метод главного критерия. Пороговая оптимизация (или метод главного критерия) Дано: По всем целям
В данной схеме предполагаем что стратегии, по которым достигается пороговое значение эффективности( Решения по которым не достигается порговое значение (хотябы по одному из локалтных критериев) неприемлимы.
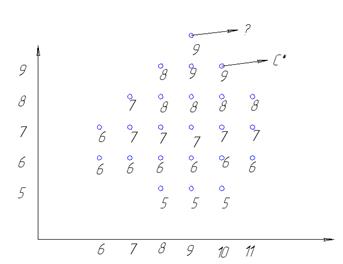
Многокритериальная оптимизация. Метод идеальной точки. Решаются m скалярных задач.
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.153 (0.009 с.) |

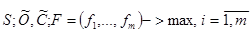
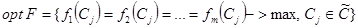



 Локальные критерии должны быть нормированы.
Локальные критерии должны быть нормированы.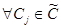 находим наихудшую оценку по всем локальным критериям.
находим наихудшую оценку по всем локальным критериям. 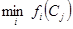 , затем находим
, затем находим 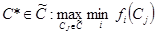 ,
, 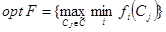
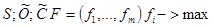
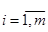
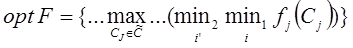
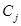 что maxmin у них одинаковый
что maxmin у них одинаковый 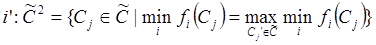
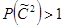 -мощность множества (число элементов)
-мощность множества (число элементов)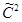 имеют максимальные минимумы, которые равны.
имеют максимальные минимумы, которые равны. Пример:
Пример:
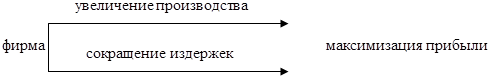
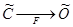 отображаются на множество оценок
отображаются на множество оценок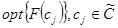 — схема компромиссов
— схема компромиссов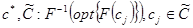

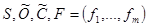 ;
; 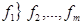 ,
, 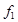 -главный критерий.
-главный критерий.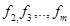 установим необходимый уровень эффективности
установим необходимый уровень эффективности 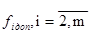 (пороговый).
(пороговый).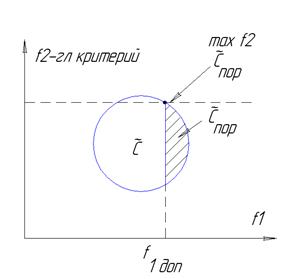
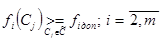 , а для первой цели производим строгую оптимизацию
, а для первой цели производим строгую оптимизацию 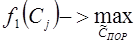
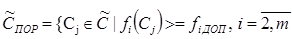
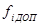 ) эквивалентны по
) эквивалентны по 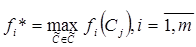
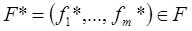 ;
; 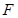 *- идеальная точка.
*- идеальная точка.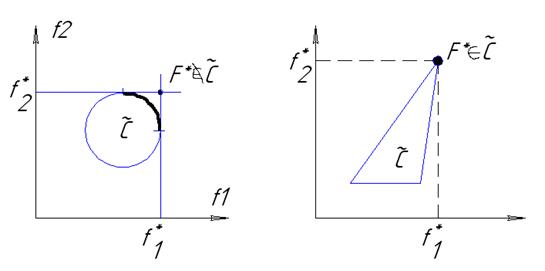

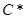 можно выбрать из пространственного соотнесения с
можно выбрать из пространственного соотнесения с 


