
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многокритериальная оптимизация, основные проблемы. Паретто-оптимальные решения.Содержание книги
Поиск на нашем сайте
Классификация ВОЗ: 1)одновекторные 2)многовекторные ВОЗ: 1) одноразмерные 2) многоразмерные ВОЗ: 1) с противоречием локальных критериев 2) без противоречия ВОЗ: 1) с выпуклойоблостью решения 2) с невыпуклойоблостью решения. Множество стратегий
Проблемы: 1) описание 2) построение схемы компромиссов opt-? 3) нормирование критериев, т.е приведение к однородности. 4) учет степени важности критериев – приоритета. Описание области решений и анализ. 1) 2) Стратегия 3) Множество всех неулучшаемых стратегий исходного множества называется множеством компромиссов, противоречий или паретто. 4) Под множество всех улучшаемых стратегий исходного множества называется областью согласия.
-интерпритация.
Ортопт – некоторое множество точек, доминирующее над данной точкой.
Вершина
Пример:
Учет приоритета критерия: некоторые схемы компромиссов требуют ранжирования компонентов по степени возможности или поиск оценок значимости критериев.
Многокритериальная оптимизация, проблемы. Метод свертки критерия. Множество стратегий
Проблемы: 1) описание 2) построение схемы компромиссов opt-? 3) нормирование критериев, т.е приведение к однородности. 4) учет степени важности критериев – приоритета.
Построение схемы компромиссов:
Дано: Свертка (или взвешанная сумма локальных критериев)
По идее wi могут быть нормирующими коэффициентами и могут учитывать возможности целей.
1)
2)
Многокритериальная оптимизация, метод уступок. Метод пошаговых уступок: Локальные цели упорядочены по степени важности Метод состоит из следующих этапов: 1)
.......... i) ............ m)
Метод абсолютных уступок.
Частное проявление этой схемы: 2) Недостатком является доминирование локальных критериев с большими абсолютными значениями эффективности (за счет коэффициента значимости это можно ослабить) Метод относительных уступок Сначала строется абсолютное изменение а потом на их базе строятся относительные изменения. Строим схему: “+”- нормировка критериев не нужна. Частные случаи: 1) 2) если нельзя перемножать то 3) если хотим учесть значимость то введем степенную функцию: 4) для логарифмической схемы с учетом значимости: “-“ – значимости критериев остаются проблемой: лучше иметь 1% от миллиона чем 10% от тысячи.
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.19.206 (0.008 с.) |

 отображаются на множестве оценок F.
отображаются на множестве оценок F. -схема компромисов. Найти
-схема компромисов. Найти 

 Стратегия
Стратегия  доминироет над стратегией
доминироет над стратегией 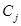
 если существует
если существует 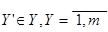 и мощность этого множества
и мощность этого множества  что
что 
 называется неулучшаемой если не существует такой стратегии
называется неулучшаемой если не существует такой стратегии 

 построение
построение 

 - локальные оценки для некоторой стратегии будем рассматривать как координаты в пространстве критериев.
- локальные оценки для некоторой стратегии будем рассматривать как координаты в пространстве критериев. строим
строим 


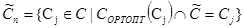 т.е точка
т.е точка 
 если ее ортопт пересекается с
если ее ортопт пересекается с  Нормировка: в общем случае в векторной задаче является разнородными. Некоторые схемы компромиссов предполагают сравнение или суммирование отдельных локальных эффективностей. Для этого должно быть 1) выбрана общая мера эффективности для этих локальных критериев(размерная или безразмерная) 2) определены свойства операций сравнения и суммирования 3) все локальные эффективности должны быть переведены в общую меру.
Нормировка: в общем случае в векторной задаче является разнородными. Некоторые схемы компромиссов предполагают сравнение или суммирование отдельных локальных эффективностей. Для этого должно быть 1) выбрана общая мера эффективности для этих локальных критериев(размерная или безразмерная) 2) определены свойства операций сравнения и суммирования 3) все локальные эффективности должны быть переведены в общую меру. ,
, 
 Строим
Строим  - вектор весовых коэффициентов.
- вектор весовых коэффициентов.  . Любая локальная цель имеет свой вес. Оценки должны быть нормированными и упорядоченными по значимости.
. Любая локальная цель имеет свой вес. Оценки должны быть нормированными и упорядоченными по значимости.


 Если область выпукла, то свертка дает решение из множества паретто.
Если область выпукла, то свертка дает решение из множества паретто.

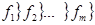

 ;
;  , находим решение
, находим решение 
 -уступка (сколько можно уступить по этому критерию?)
-уступка (сколько можно уступить по этому критерию?)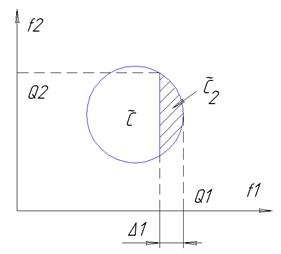 2)
2)  , находим решение скалярной задачи:
, находим решение скалярной задачи:  ,
,  -уступка
-уступка , находим решение скалярной задачи:
, находим решение скалярной задачи:  ,
,  -уступка
-уступка
 если мы переходим из
если мы переходим из  то это связано с изменением локальных критериев.
то это связано с изменением локальных критериев.  если
если  , если нет то
, если нет то  . При
. При  -множество индексов) а по каким-то ухужшение (
-множество индексов) а по каким-то ухужшение ( -множество индексов)
-множество индексов) ;
;  ;
;  , при этом критерии должны быть нормированы!!!.
, при этом критерии должны быть нормированы!!!. если если учитываем значимость цели, вводим коэффициент значимости
если если учитываем значимость цели, вводим коэффициент значимости  :
:
 если
если 
 если суммарные относительные улучшения превосходят суммарные относительные ухудшения, то переход целесообразен.
если суммарные относительные улучшения превосходят суммарные относительные ухудшения, то переход целесообразен.






