
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема метода ветвей и границ.Содержание книги
Поиск на нашем сайте
Основной идеей любых комбинированных методов является замена полного перебора всех возможных планов (решений) их частичным перебором. По сравнению с методами отсечения комбинаторные методы значительно меньше подвержены влиянию ошибок округления.комбинаторные методы характеризуются более простыми арифметическими операциями, но более сложной логической структурой. Большинство комбинаторных методов не нуждаются в специальном доказательстве своей конечности, за исключением тех методов, которые являются процессами направленного перебора с «возвращениями» (например метод Балаша). Наиболее распространенными среди комбинаторных методов являются объединяемее общим названием «метод ветвей и границ». Впервые метод ветвей и границ был предложен в 1960 г. Основное содержание метода. Рассмотри задачу дискретного программирования: (3.9) где G – некоторое конечное множество. В основе метода лежит выполнение нескольких этапов решения задачи: 1) Вычисление нижней границы (оценки). Часто можно указать, вычислить нижнее значение целевой функции на множестве планов Gили на его подмножестве 2) ветвление (разбиение множества планов Gна подмножества). Ветвление, то есть построение дерева подмножеств, происходит по такой многошаговой процедуре: 0-й шаг: имеется множество
3) пересчет границ (оценок): Очевидно, что если Поэтому при разбиении 4) Вычисление планов. Способ вычисления планов в последовательно разветвляемых подмножествах в сильной степени зависит от операции конкретной задачи. 5) признак оптимальности. Пусть 6) оценка точности приближенного решения. И так, при Алгоритм метода ветвей и границ: 0-й шаг: вычисляем 1-ый шаг: вычисляем Если же оптимальный план не найден, то выбирается «наиболее перспективное» для дальнейшего разбиения множеств
k-ый шаг ( 32 Метод ветвей и границ, решение линейных целочисленных задач.(Метод Ленд и Дойг)
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 886; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

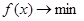 (3.10)
(3.10) 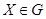
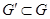 , то есть найти такое число
, то есть найти такое число  (или
(или  ), что для любого
), что для любого 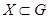 имеет место
имеет место  (или для любого
(или для любого 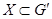 имеет место
имеет место 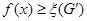 ).
). . Некоторым образом оно разбивается на конечное число (обычно не пересекающихся) подмножеств:
. Некоторым образом оно разбивается на конечное число (обычно не пересекающихся) подмножеств:  .
. k-ый шаг
k-ый шаг 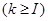 : имеются множества
: имеются множества 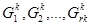 , еще не подвергавшихся ветвлению. П о определенному правилу среди них выбирается одно множество
, еще не подвергавшихся ветвлению. П о определенному правилу среди них выбирается одно множество  , и оно разбивается на конечное число подмножеств
, и оно разбивается на конечное число подмножеств  . Еще не подвергавшихся разбиению множества
. Еще не подвергавшихся разбиению множества  , обозначаются через
, обозначаются через  . Пример нескольких шагов такого процесса разбиения показан на рис 3.1.
. Пример нескольких шагов такого процесса разбиения показан на рис 3.1.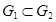 , то
, то 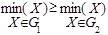
 на
на 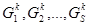 :
: 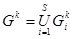 , всегда будим иметь в виду, что граница (оценка) для любого подмножества
, всегда будим иметь в виду, что граница (оценка) для любого подмножества  не меньше оценки
не меньше оценки 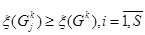 . В некоторых случаях, когда удается хотя бы для отдельных iполучить строгое неравенство
. В некоторых случаях, когда удается хотя бы для отдельных iполучить строгое неравенство  , то можно значительно сократить число вычислений в процессе решения той или иной задачи.
, то можно значительно сократить число вычислений в процессе решения той или иной задачи. и план Х принадлежит некоторому подмножеству
и план Х принадлежит некоторому подмножеству  . Если при этом
. Если при этом 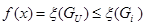 ,
,  , то Х является оптимальным планом задачи (3.9), (3.10).
, то Х является оптимальным планом задачи (3.9), (3.10).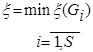 . Тогда, если
. Тогда, если 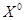 - некоторый план исходной задачи (
- некоторый план исходной задачи (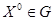 ),
), 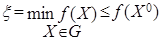 (доказательство непосредственно следует из определения оценки). Очевидно, что если разность
(доказательство непосредственно следует из определения оценки). Очевидно, что если разность 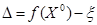 невелика (то есть порог задан), то
невелика (то есть порог задан), то  - за оценку точности приближения.
- за оценку точности приближения.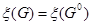 , если при этом удается найти такой план Х, что
, если при этом удается найти такой план Х, что  , то
, то 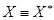 - оптимальный план. Если оптимальный план не найден, то некоторым способом разбиваем
- оптимальный план. Если оптимальный план не найден, то некоторым способом разбиваем 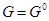 на конечное число подмножеств
на конечное число подмножеств  и переходим к шагу 1.
и переходим к шагу 1. . Если при этом удается найти такой план Х что
. Если при этом удается найти такой план Х что 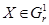 , для некоторого r (
, для некоторого r (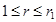 ) и
) и 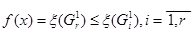 , то
, то 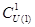 , по следующему правилу:
, по следующему правилу: 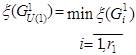 Разбиваем множество
Разбиваем множество 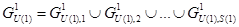 . Если не подвергавшиеся разбиению множества
. Если не подвергавшиеся разбиению множества заново обозначаем через
заново обозначаем через 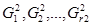 и переходим к шагу 2.
и переходим к шагу 2. ): вычисляем оценки
): вычисляем оценки  . Если при этом удается найти такой план Х, что
. Если при этом удается найти такой план Х, что  , для некоторого r (
, для некоторого r (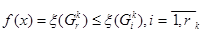 , то
, то 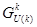 , по правилу:
, по правилу: 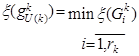 . Разбиваем это множество на несколько непересекающихся подмножеств
. Разбиваем это множество на несколько непересекающихся подмножеств  . Затем еще не подвергавшиеся разбиению множества
. Затем еще не подвергавшиеся разбиению множества 





