
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическое программирование, принцип Беллмана, схема метода.Содержание книги
Поиск на нашем сайте
ДП – математический метод оптимизации многошаговых процессов принятия решений. ДП является инструментом приведения многомерных задач к многошаговым одномерным (меньшей размерности). Решение – не точечная акция (во времени и пространстве), а последовательность шагов (этапов), на каждом из которых принимается некоторое решение, определяющее изменение состояния системы на каждом шаге. В некоторых задачах этапы являются естественными и вытекают из сущности задачи. В других задачах шаги вводятся искусственно, чтобы для решения можно было применить метод ДП. Задачи ДП: · распределение ресурсов; · календарное планирование; · управление запасами; · оптимизация маршрутов на сетях; · замена оборудования. В ДП проводится оптимизация общего решения, получаемого на всех шагах, а не на каждом шаге в отдельности. Постановка задачи: Имеется система S, которая переходит из начального состояния S0 в конечное состояние Sm под воздействием вектора управлений U. В развернутом виде это выглядит:
Или сокращенно:
Где Все эти переходы можно представиться как траекторию в фазовом пространстве:
(Рисунок рассмотрен для случая, когда состояния системы описываются двумерным вектором). Управление тоже может описываться вектором. Через Также кроме аддитивного критерия может применяться мультипликативный, где При решение задач методом ДП основой является уравнение Беллмана. Уравнение Беллмана справедливо для систем, в которых выполняется принцип оптимальности Беллмана: «каково бы ни было состояние перед некоторым шагом, мы на данном шаге и всех последующих должны выбирать управление, обеспечивающее оптимальную траекторию движения в конечное состояние, независимо от того, как мы попали в это состояние». Существенным является то, что выигрыш, который можно получить из текущего состояния не зависит от того, каким образом мы попали в это состояние. Таким образом, доход на данном шаге зависит только от текущего состояния и выбранного управления. Рассмотрим последовательность переходов состояний в виде следующей схемы:
Доход на i – м шаге:
Назовем конструкцию
где ui – все возможные управления на i-м шаге, Si – получается из функции перехода состояний Реализация вышеописанных идей предполагает 2 этапа: 1. Обратная прогонка. m-й шаг:
m-1-й шаг:
………………………………………………………………………….. i-йшаг:
………………………………………………………………………….. 1-йшаг:
2. Прямая прогонка. В результате обратной прогонки получили УОВ на 1-м шаге. Нулевое состояние системы, при котором УОВ на 1-м шаге максимален и есть оптимальный выигрыш данной задачи. На каждом шаге было сформировано условно оптимальное управление. Определив начальное состояние, приводящее к оптимальному выигрышу (зачастую мощность множества начальных состояний равна единице, т.е. начальное состояние заранее известно), по УОУ на 1-м шаге определим соответствующее управление, которое уже будет безусловным. Имея управление на 1-м шаге и начальное состояние, по функции перехода состояний получим 1-е состояние, по которому определим безусловное оптимальное управление на 2-м шаге. И так далее восстановим всю цепочку оптимальных управлений. Сказанное можно записать следующим образом:
35. Динамическое программирование. Задача распределения капиталовложений (ресурсов). Имеется m предприятий П1, П2, …, Пm. K0 – средства, вкладываемые в развитие этих предприятий. Пусть xi – вклад в i – е предприятие. В результате этого вклада имеем доход Vi(xi). Задача состоит в том, чтобы распределить начальные средства K0так, чтобы суммарный доход от всех предприятий был максимален.
Для решения задачи данной задачи необходимо: · сформировать шаги; · решить, что есть управление; · сформировать оценки управлений.
В качестве шагов будем рассматривать вклад ресурса в конкретное предприятие. Состояние будет описываться количеством оставшегося ресурса к концу шага
Обратная прогонка: m-й шаг:
с учетом требования к трате всего ресурса на последнем шаге получаем:
………………………………………………………………………….. i-й шаг:
………………………………………………………………………….. 1-й шаг:
Прямаяпрогонка:
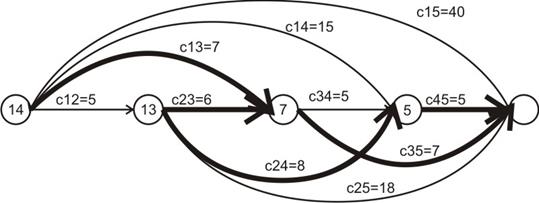
36. Динамическое программирование. Задача о замене оборудования (1-я постановка). Оборудование эксплуатируется в течение некоторого количества шагов. На каждом шаге можно принять решение: заменить оборудование или продолжить его эксплуатацию на следующем шаге. Замена и эксплуатация стоят некоторых ресурсов. Эксплуатация нового оборудования стоит меньше, чем старого. Требуется построить оптимальный план замены оборудования, чтобы суммарные затраты на эксплуатацию и замену были минимальны. В 1-й постановке это задачи считаем, что оборудование не имеет остаточной стоимости (то есть при замене старое оборудование нельзя продать) и затраты на замену и эксплуатацию не разделяются.
На дугах показаны затраты на замену и эксплуатацию оборудования, цифры в вершинах обозначают начало соответствующего шага.Состояние описывается только лишь номером шага, поэтому будем обозначать условно оптимальный выигрыш Обратная прогонка: n-й шаг:
n-1-йшаг:
………………………………………………………………………….. i-йшаг:
………………………………………………………………………….. 1-й шаг:
Разберем обратную и прямую прогонки на конкретном примере. Оптимальное управление будем отмечать жирной стрелкой. Вместо начала шагов в вершинах будем писать условно оптимальный выигрыш. Последний 4-й шаг тривиален, как и описано в общей схеме (на первых картинка косяк, должно быть 4-й шаг:
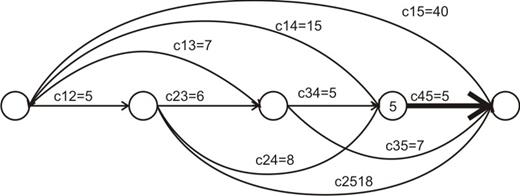
3-й шаг: на начале 3-го шага альтернативы 2: сразу попасть в конечное состояние или сначала перейти в предпоследнее состояние:
То есть выгоднее сразу перейти в конечное состояние:
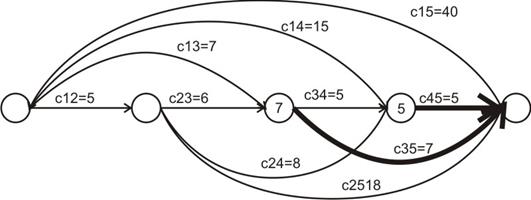
2-й шаг:
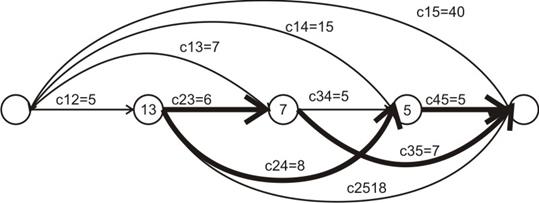
1-й шаг:
Прямая прогонка – переход по жирным дугам из начала в конец:
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.233.83 (0.01 с.) |

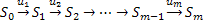
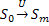
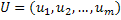 – вектор управлений.
– вектор управлений.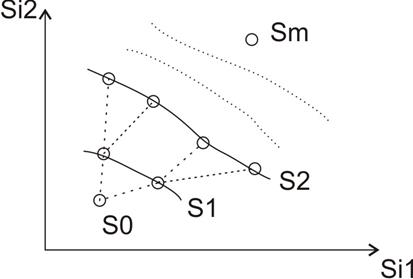
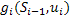 – будем обозначать доход на переходе
– будем обозначать доход на переходе 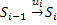 ,
, 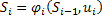 - функция перехода состояний. Интересующий нас выигрыш –
- функция перехода состояний. Интересующий нас выигрыш – 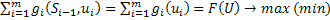
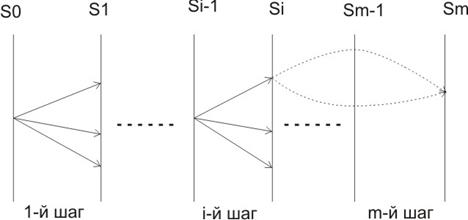
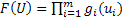 .
.
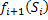 – наилучшая эффективность при движении из Si в Sm– называется Условно Оптимальным Выигрышем (УОВ). УОВ зависит только от состояния, это непосредственно вытекает из формулы для УОВ. Управление, при котором достигается УОВ называется Условно Оптимальным Управлением (УОУ) и обозначается
– наилучшая эффективность при движении из Si в Sm– называется Условно Оптимальным Выигрышем (УОВ). УОВ зависит только от состояния, это непосредственно вытекает из формулы для УОВ. Управление, при котором достигается УОВ называется Условно Оптимальным Управлением (УОУ) и обозначается 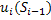 .
.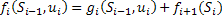 – полуоптимальным выигрышем (ПОВ). В таком случае УОВ на i-м шаге будет иметь вид (Уравнение Беллмана):
– полуоптимальным выигрышем (ПОВ). В таком случае УОВ на i-м шаге будет иметь вид (Уравнение Беллмана):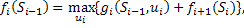
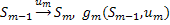
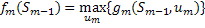 , где
, где 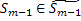 – множество возможных «предпоследних» состояний.
– множество возможных «предпоследних» состояний.  - УОУ.
- УОУ.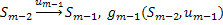
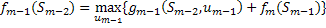 , где
, где 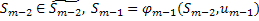 .
. 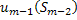 – УОУ. УОВ
– УОУ. УОВ 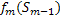 – полученна предыдущем шаге.
– полученна предыдущем шаге.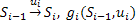
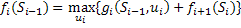 , где
, где 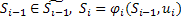 .
. 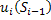 – УОУ.
– УОУ.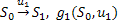
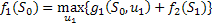 , где
, где 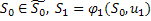 .
. 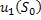 – УОУ.
– УОУ.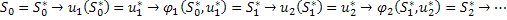
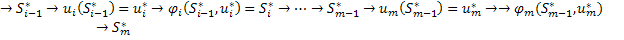
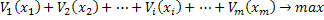
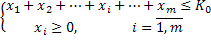
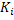 . Величина вклада будет выступать управлением, оценка управления – выигрыш от вложения средств в предприятие. Функция перехода состояний количество ресурса в начала шага вычесть вкладываемый ресурс:
. Величина вклада будет выступать управлением, оценка управления – выигрыш от вложения средств в предприятие. Функция перехода состояний количество ресурса в начала шага вычесть вкладываемый ресурс: 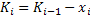 . Будем считать, что
. Будем считать, что 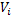 монотонно возрастают, тогда очевидно, что максимальный выигрыш будет достигнут только при распределении имеющегося ресурса без остатка. Нарисуем схему переходов состояний с отображением управлений и выигрышей:
монотонно возрастают, тогда очевидно, что максимальный выигрыш будет достигнут только при распределении имеющегося ресурса без остатка. Нарисуем схему переходов состояний с отображением управлений и выигрышей:
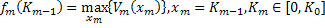
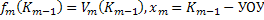




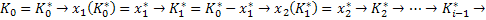
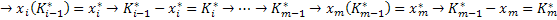
 – затратына замену и эксплуатацию оборудования, начиная с
– затратына замену и эксплуатацию оборудования, начиная с 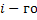 шага, заканчивая началом
шага, заканчивая началом 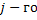 шага. То есть,
шага. То есть, 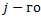 шага. Эти затраты известны по условию задачи. Нарисуем схему задачи для 4 этапов эксплуатирования оборудования:
шага. Эти затраты известны по условию задачи. Нарисуем схему задачи для 4 этапов эксплуатирования оборудования:
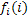 просто как
просто как  .
.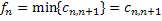
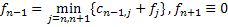
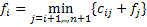

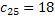 ).
).

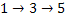 .
.


