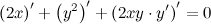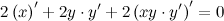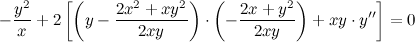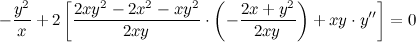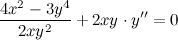Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частное и полное приращения функции нескольких переменных. Частные производные и частные дифференциалы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть задана функция z = f(х, у). Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять постоянное значение. Дадим переменной х приращение ∆х, сохраняя значение переменной у неизменным. Тогда функция z получит приращение, которое назовем частным приращением z по х и обозначим ∆х z: ∆х z = f(x + ∆x, y) – f(х, у). Наконец, если аргументу х дать приращение ∆х, а аргументу у – приращение ∆у, то получим полное приращение функции z: ∆ z=f(x+∆x, y+∆у)–f(х, у). Частная производная-производная по одной из переменных в функции нескольких переменных, только в ней все остальные переменные принимаются за константы, а потом находится производная. С дифференциалом то же самое, но только находится интеграл. Дифференцируемость функции. Полный дифференциал. Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Главная часть приращения функции, линейная относительно приращения переменных, называется полным дифференциалом. dZ или df(x,y,z...) Дифференцирование сложной ФНП. Производные неявных функций. Теорема.Пусть u = f (х, у) задана в области D и пусть х = х(t) и у = у(t) определены в области
Доказательство.Так как u дифференцируема по условию в точке (x0, y0), то её полное приращение представляется в виде
Разделив это соотношение на
Перейдём к пределу при
Замечание 1.Если u = u(x, y) и x = x, y = y(x), то полная производная функции u по переменной х
Последнее равенство можно использовать для доказательства правила дифференцирования функции одной переменной, заданной неявно в виде F(x, y) = 0, где y = y(x) (см. тему № 3 и пример 14). Имеем: Вернёмся к примеру 14 темы № 3:
Как видим, ответы совпали. Задание. Найти вторую производную Решение. Продифференцируем левую и правую часть заданного равенства, при этом помним, что
Из полученного равенства выражаем
Для нахождения второй производной продифференцируем равенство
Подставив вместо
После упрощения получаем:
Из полученного равенства выражаем вторую производную
Ответ.
Производная по направлению. Производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления. Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению. 6. Уравнения касательной плоскости и нормали к поверхности z=F(x,y). Касательная плоскость в точке гладкой поверхности — это плоскость, имеющая максимальный порядок соприкосновения с поверхностью в этой точке. Эквивалентный вариант определения: касательная плоскость есть плоскость, содержащая касательные ко всем гладким кривым, проходящим через эту точку. F(x,y,z) = √(x^2+y^2) - z
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.78 (0.01 с.) |

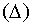 , причём, когда
, причём, когда 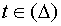 , то х и у принадлежат области D. Пусть функция u дифференцируема в точке M0(x0, y0, z0), а функции х(t) и у(t) дифференцируемы в соответствующей точке t0, то сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t0 и имеет место равенство:
, то х и у принадлежат области D. Пусть функция u дифференцируема в точке M0(x0, y0, z0), а функции х(t) и у(t) дифференцируемы в соответствующей точке t0, то сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t0 и имеет место равенство: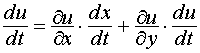 .
. .
.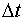 , получим:
, получим: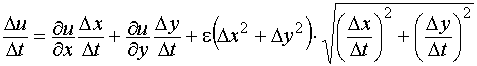 .
.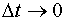 и получим формулу
и получим формулу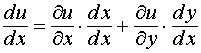 или
или 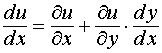 .
.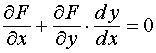 . Отсюда
. Отсюда  . (6.1)
. (6.1) ;
;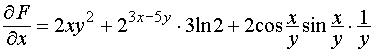 ;
;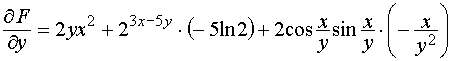 ;
;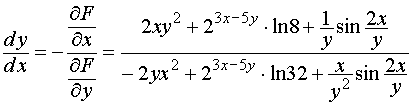 .
. неявной функции
неявной функции 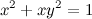 .
.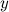 является функцией переменной
является функцией переменной  , поэтому производную от нее будем брать как производную от сложной функции. В итоге получаем:
, поэтому производную от нее будем брать как производную от сложной функции. В итоге получаем: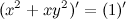
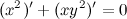
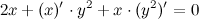
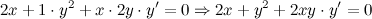
 :
:
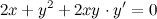 еще раз:
еще раз: