
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная ФКП. Условия Коши-Римана. Аналитические функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие функции комплексной переменной Сначала освежим знания о школьной функции одной переменной: Функция одной переменной В комплексном случае функциональная зависимость задается аналогично: Однозначная функция комплексной переменной Чем отличается функция комплексной переменной? Главное отличие: числа комплексные. Я не иронизирую. От таких вопросов нередко впадают в ступор, в конце статьи историю прикольную расскажу. На уроке Комплексные числа для чайников мы рассматривали комплексное число в виде Действительная и мнимая часть функции комплексной переменной Функцию комплексной переменной можно записать в виде: Функция То есть, функция комплексной переменной Пример 1 Найти действительную и мнимую часть функции Решение: Независимая переменная «зет», как вы помните, записывается в виде (1) В исходную функцию (2) Для первого слагаемого использовали формулу сокращенного умножения (3) Аккуратно возвели в квадрат (4) Перегруппировка слагаемых: сначала переписываем слагаемые, в которых нет мнимой единицы (первая группа), затем слагаемые, где есть (5) У второй группы выносим В результате наша функция оказалась представлена в виде Ответ: Что это получились за функции? Самые что ни на есть обыкновенные функции двух переменных, от которых можно найти такие популярные частные производные. Без пощады – находить будем. Но чуть позже. Кратко алгоритм прорешанной задачи можно записать так: в исходную функцию подставляем Пример 2 Найти действительную и мнимую часть функции Это пример для самостоятельного решения. Перед тем как с шашками наголо броситься в бой на комплексной плоскости, позвольте дать самый важный совет по теме: БУДЬТЕ ВНИМАТЕЛЬНЫ! Внимательным нужно быть, конечно, везде, но в комплексных числах следует быть внимательным, как никогда! Помните, что Полное решение и ответ в конце урока. Чтобы дальше легче жилось, обратим внимание на пару полезных формул. В Примере 1 было выяснено, что Теперь куб. Используя формулу сокращенного умножения Рекомендую переписать в тетрадь две рабочие формулы: Формулы очень удобно использовать на практике, поскольку они значительно ускоряют процесс решения.
Дифференцирование функций комплексной переменной. У меня есть две новости: хорошая и плохая. Начну с хорошей. Для функции комплексной переменной Плохая новость состоит в том, что для многих функций комплексной переменной производной не существует вообще, и приходится выяснять, дифференцируема ли та или иная функция. А «выяснять», как чует ваше сердце, связано с дополнительными заморочками. Рассмотрим функцию комплексной переменной 1) Чтобы существовали частные производные первого порядка 2) Чтобы выполнялись так называемые условия Коши-Римана: Только в этом случае будет существовать производная! Пример 3 Определить действительную Решение раскладывается на три последовательных этапа: 1) Найдём действительную и мнимую часть функции. Данное задание было разобрано в предыдущих примерах, поэтому запишу без комментариев: Так как Таким образом: Остановлюсь еще на одном техническом моменте: в каком порядке записывать слагаемые в действительной и мнимой частях? Да, в принципе, без разницы. Например, действительную часть можно записать так: 3) Проверим выполнение условий Коши Римана. Их два. Начнем с проверки условия Несомненно, приятная новость – частные производные почти всегда очень простые. Проверяем выполнение второго условия Условия Коши-Римана выполнены, следовательно, функция дифференцируема. 3) Найдём производную функции. Производная тоже очень простая и находится по обычным правилам: Мнимая единица при дифференцировании считается константой. Ответ:
Интеграл ФКП. Теорема Коши.
Формула (52) называется интегральной формулой Коши или интегралом Коши. Если в качестве контура
Формула Коши может быть расширена для производных аналитической функции
Помимо самостоятельного значения интегральной формулы Коши, (52), (54) фактически дают очень удобный способ вычисления контурных интегралов, которые, как видно, будут выражаться через значение "остатка" подынтегральной функции в точке, где эта функция имеет особенность Пример 3-9. Вычислить интеграл от функции Решение. Точка
Формула Коши. Пусть
Формула справедлива также, если предполагать, что Элементарные ФКП: функция Тейлора, тригонометрические функции, гиперболические функции, обратные тригонометрические функции, логарифмические функции, формула Коши.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.13.119 (0.008 с.) |

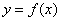 – это правило, по которому каждому значению независимой переменной
– это правило, по которому каждому значению независимой переменной  (из области определения) соответствует одно и только одно значение функции
(из области определения) соответствует одно и только одно значение функции  . Естественно, «икс» и «игрек» – действительные числа.
. Естественно, «икс» и «игрек» – действительные числа. – это правило, по которому каждому комплексному значению независимой переменной
– это правило, по которому каждому комплексному значению независимой переменной  (из области определения) соответствует одно и только одно комплексное значение функции
(из области определения) соответствует одно и только одно комплексное значение функции  . В теории рассматриваются также многозначные и некоторые другие типы функций, но для простоты я остановлюсь на одном определении.
. В теории рассматриваются также многозначные и некоторые другие типы функций, но для простоты я остановлюсь на одном определении. . Поскольку сейчас буква «зет» стала переменной, то её мы будем обозначать следующим образом:
. Поскольку сейчас буква «зет» стала переменной, то её мы будем обозначать следующим образом:  , при этом «икс» и «игрек» могут принимать различные действительныезначения. Грубо говоря, функция комплексной переменной
, при этом «икс» и «игрек» могут принимать различные действительныезначения. Грубо говоря, функция комплексной переменной  зависит от переменных
зависит от переменных  , где
, где  и
и  – две функции двух действительных переменных.
– две функции двух действительных переменных. называется мнимой частью функции
называется мнимой частью функции  и
и  . Чтобы окончательно всё прояснить рассмотрим практические примеры:
. Чтобы окончательно всё прояснить рассмотрим практические примеры:
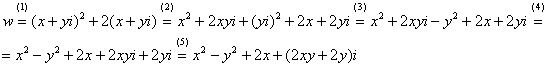
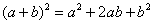 . В слагаемом
. В слагаемом  – раскрыли скобки.
– раскрыли скобки. , не забывая, что
, не забывая, что 
 (вторая группа). Следует отметить, что перетасовывать слагаемые не обязательно, и данный этап можно пропустить (фактически выполнив его устно).
(вторая группа). Следует отметить, что перетасовывать слагаемые не обязательно, и данный этап можно пропустить (фактически выполнив его устно). – действительная часть функции
– действительная часть функции  – мнимая часть функции
– мнимая часть функции 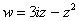
 .
. , выведем:
, выведем: .
.
 . Об этих обозначениях сразу забудьте, поскольку в теории функции комплексного переменного традиционно используется другой вариант записи:
. Об этих обозначениях сразу забудьте, поскольку в теории функции комплексного переменного традиционно используется другой вариант записи:  .
.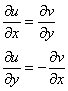
 и мнимую
и мнимую  части функции
части функции  . Проверить выполнение условий Коши-Римана. В случае выполнения условий Коши-Римана, найти производную функции.
. Проверить выполнение условий Коши-Римана. В случае выполнения условий Коши-Римана, найти производную функции.
 – действительная часть функции
– действительная часть функции  ;
; – мнимая часть функции
– мнимая часть функции  , а мнимую – так:
, а мнимую – так:  .
. . Находим частные производные:
. Находим частные производные:
 :
:
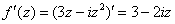
 .
. во внутренних точках области ее определения и граничными значениями. При этом имеет место следующее соотношение (рис.19):
во внутренних точках области ее определения и граничными значениями. При этом имеет место следующее соотношение (рис.19):

 в (52) выбрать окружность
в (52) выбрать окружность 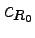 , то, заменяя
, то, заменяя  и учитывая, что
и учитывая, что  - дифференциал длины дуги
- дифференциал длины дуги 
 входит в интеграл (52) как параметр, то на основе свойств интегралов, зависящих от параметра, после
входит в интеграл (52) как параметр, то на основе свойств интегралов, зависящих от параметра, после  -кратного дифференцирования, можно получить
-кратного дифференцирования, можно получить
 .
. по контуру
по контуру  (рис.20).
(рис.20). , в которой функция
, в которой функция  имеет особенность, в отличие от примера 4-1, находится внутри окружности
имеет особенность, в отличие от примера 4-1, находится внутри окружности  . Представим интеграл в форме (52):
. Представим интеграл в форме (52):

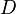 — область на комплексной плоскости с кусочно-гладкой границей
— область на комплексной плоскости с кусочно-гладкой границей  , функция
, функция  — голоморфна в
— голоморфна в 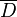 и
и  — точка внутри области
— точка внутри области 



