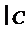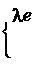Дисперсія та середнє квадратичне відхилення

 

Математичне сподівання не дає достатньо повної інформації про випадкову величину, оскільки одному й тому самому значенню М (Х) може відповідати безліч випадкових величин, які будуть різнитися не лише можливими значеннями, а й характером розподілу і самою природою можливих значень.

Математичне сподівання називають центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією.

Для визначення дисперсії розглядається відхилення випадкової величини X від свого математичного сподівання (X − M (X)).

 

Дисперсією випадкової величини X називається математичне сподівання квадрата відхилення цієї величини

D (X) = M (X − M (X))2 (5.3) Для дискретної випадкової величини X дисперсія:

 

n

D (X) = (xi − M (X))2 (5.4) i =1

 

47

å

 

для неперервної:

 

¥

D (X)=ò(x − M (X))2 dx (5.5)−¥

 

Властивості дисперсії:

 

1. Якщо С – стала величина, то D (C) = C.

 

2. D (СХ) = C 2 D (X).

 

 

3. Якщо А і В є сталими величинами, то

 

D (A + BX) = B 2 M (X)

 

Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті.

Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Такою числовою характеристикою є середнє квадратичне відхилення.

Середнім квадратичним відхиленням випадкової величини X

 

називають корінь квадратний із дисперсії:

 

s(X) = D (X) (5.6)

 

Початкові та центральні моменти

 

Узагальненими числовими характеристиками випадкових величин є початкові та центральні моменти.

Початковим моментом k -го порядку випадкової величини X називають математичне сподівання величини X k:

n k = M (X k).

	å
		i

 

Для ДВВ:

 

для НВВ:

n k = nxkpi, i =1

 

¥

n k =ò xkf (x) dx. −¥

 

 

 

Центральним моментом k -го порядку випадкової величини X називають математичне сподівання від (X − M (X)) k:

 

m k = M (X − M (X)) k. 1.5. Асиметрія і ексцес

Третій центральний момент характеризує асиметрію закону

 

розподілу випадкової величини. Якщо m3= 0, то випадкова величина X симетрично розподілена відносно М (Х). Оскільки m3 має розмірність випадкової величини в кубі, то вводять безрозмірну

 

величину — коефіцієнт асиметрії: As =m3.

 

Центральний момент четвертого порядку використовується для визначення ексцесу, що характеризує плосковершинність, або гостровершинність щільності ймовірності f (x). Ексцес обчислюється

 

за формулою

 

Es =m4−3.

 

 

2. Біноміальний закон розподілу Цей закон має вигляд

P (X = m) = Cmpm (1− p) n − m, m = 0,1,2,..., n (5.7) і використовується у схемі Бернуллі, тобто у випадку n незалежних повторних випробувань, в кожному з яких деяка подія з'являється з

ймовірністю р.

 

Для біноміального розподілу: M (X) = np, D (X) = npq.

 

 

Закон розподілу Пуассона

 

ДВВ X приймає злічену множину значень (m = 0,1,2,....) з

 

ймовірностями

 

P (X = m) = ame − a. (5.8)

 

 

49

s

s

n

m

!

 

Цей розподіл використовують в задачах статистичного контролю якості, в теорії надійності, теорії масового обслуговування, для обчислення: кількості вимог на виплату страхових сум за рік,

кількості дефектів однакових виробів.

 

Для розподілу Пуассона: M (X) = a, D (X) = a.

 

 

Рівномірний розподіл

 

Означення 1. НВВ X розподілена рівномірно на проміжку (a, b), якщо усі її можливі значення належать цьому проміжку і

 

щільність її ймовірностей на цьому проміжку стала, тобто

=

,

ï

ì 1

f (x) = í b − a

î0,

 

x Î(a, b); (5.9) x Ï(a, b).

 

Величина сталої С визначається умовою нормування

 

P (a < X < b) = C (b − a) =1.

 

 

Цей розподіл задовольняють, наприклад, похибки округлення різноманітних розрахунків.

Числовими характеристиками НВВ X, що розподілена за рівномірним законом, будуть

M (X) = b + a, D (X) = (b − a)2.

 

Експоненціальний розподіл

 

Означення 2. Випадкову величину X називають розподіленою за експоненціальним законом, якщо щільність її ймовірностей має вигляд

f (x) = ì0,−l x,

 

x ³ 0;

 

x < 0.

 

 

(5.10)

 

де l > 0 - параметр.

 

Експоненціальному розподілу задовольняють: час телефонної розмови, час ремонту техніки, час безвідмовної роботи комп'ютера.

 

 

 

Числовими характеристиками експоненціального розподілу будуть M (X) = 1, D (X) = 1.

 

 

Нормальний розподіл

 

Означення 3. Випадкову величину X називають розподіленою нормально, якщо щільність її ймовірностей має вигляд

f (x) = s1 p e −(x − a)2. (5.11)

 

Графік цієї функції f (x) називають нормальною кривою або кривою Гауса.

 

Для цього розподілу: M (X) = a, D (X) =s2.

 

Отже, математичне сподівання нормального розподілу дорівнює

 

параметру а цього розподілу, а середнє квадратичне відхилення дорівнює параметру s.

 

Зауваження. Якщо випадкова величина Х розподілена за нормальним законом з параметрами а та s, то випадкова величина

l

=

Z

å

i

X − a s

 

буде розподілена за нормованим нормальним законом і

 

M (Z) = 0, s(Z) =1.

 

 

7. Розподіл c2 («хі-квадрат»)

 

Нехай Xi (i =1,2,..., n) - нормальні, нормовані незалежні величини, тобто їх математичне сподівання дорівнює нулю, середнє квадратичне відхилення дорівнює одиниці і кожна з них розподілена за нормальним законом. Тоді сума квадратів цих величин

c2 = nX 2 i =1

 

 

розподілена за законом c2 з k = n степенями вільності.

 

Якщо величини Xi зв'язані одним лінійним співвідношенням,

 

n

наприклад, Xi = nX, то число ступенів свободи буде k = n −1. i =1

 

Зауважимо, що розподіл c2 визначається параметром – числом ступенів свободи k. Коли k зростає, розподіл c2 прямує до нормального розподілу дуже повільно.

 

Розподіл Стьюдента

 

Нехай X - нормальна нормована випадкова величина, а Y -незалежна від X величина, яка розподілена за законом хі-квадрат з k степенями свободи. Тоді величина

	å

 

T =

X

 

Y

 

k

 

має розподіл, який називають t розподілом або розподілом Стьюдента (це є псевдонім англійського статистика Вільяма Госсета) з

k степенями вільності.

 

При зростанні k розподіл Стьюдента швидко наближується до нормального розподілу.

 

 

Питання для самоконтролю

 

1. Визначення нормального закону розподілу.

 

2. Як впливають параметри a, s на графіки функцій f(x), F(x) загального нормального закону.

3. Що називають нормованим нормальним законом?

 

4. Чому дорівнює Мо і Ме для нормального закону розподілу? 5. Навести визначення m3для нормального розподілу.

 

Література Обов’язкова: [1]. Додаткова:[1], [4], [7].