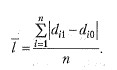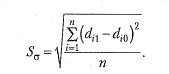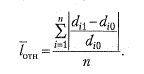Показатели для обобщённой характеристики структурных изменений.

Эти показатели дают представления о величине структурных изменений, но не дают их характеристику

Среднее линейное изменение долей

 

Среднее квадратическое изменение

 

Средняя оценка меры изменений (на одну группу, единицу совокупности) представлена средним линейным изменением долей или средним квадратическим этих изменений. Полученные значения показывают, на сколько процентных пунктов в среднем отклоняются друг от друга удельные веса сравниваемых структур.

Аналитическое содержание этих двух показателей одинаково. Однако средняя квадратическая всегда больше, чем средняя арифметическая, поэтому значение среднеквадратического изменения будет больше, чем среднего линейного.

Два показателя будут равны в том случае, если абсолютные изменения удельных весов всех частей целого по своему абсолютному значению равны. При отсутствии изменений в структурах эти показатели равны нулю.

При использовании перечисленных показателей анализ изменения структур происходит без учета величины базы, от которой это изменение произошло. Более точную оценку может дать использование не абсолютных, а относительных изменений. В частности, можно рассчитать среднее относительное линейное изменение как среднюю величину из относительных линейных отклонений (т.е. темпов прироста), взятых по модулю:

Результат умноженный на 100 будет выражен в процентах и может быть оценен.

Показатели дифференциации. Квантили, децильный коэффициент, коэффициент фондов.

1. Значения признака, которые делят все единицы распределения на равные численности, получили название квантилей или градиентов. Квартили, квинтили, децили, перцентили – это частные случаи квантилей. Квинтили делят распределение на пять равных частей. Дециль – такое значение признака в ряду распределения, которому соответствуют десятые доли численности совокупности. Перцентили делят распределение на 100 равных частей. Квартилями называют такие значения признака, которые делят распределение на четыре равные части.

Идея построения квантилей – расширить понятие медианы. С этой точки зрения медиана представляет собой центральный квартиль.

Если обозначить значения xi, делящие вариационный ряд на четыре равные части, через Q1, Q2, Q3, то ниже первого квартиля лежит ¼ значений xi, ¾ элементов совокупности имеют значения xi, превышающие Q1. Второй квартиль делит распределение пополам и совпадает с медианой. Между медианой и третьим квартилем Q3 располагается 1/4 всей совокупности, и наконец, 1\4 значений лежит выше Q3. При этом Q3 называют верхним квартилем, а Q1 нижним квартилем.

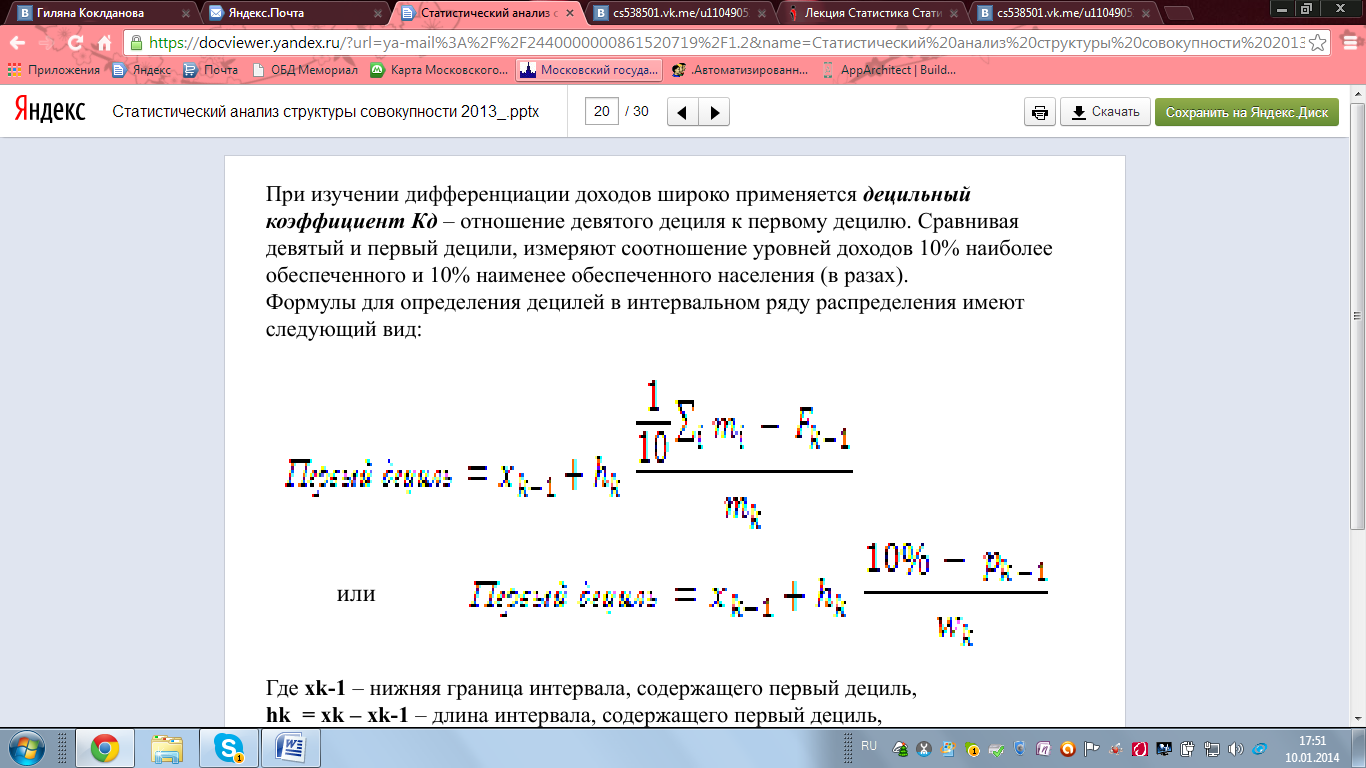
2. При изучении дифференциации доходов широко применяется децильный коэффициент Кд – отношение девятого дециля к первому децилю. Сравнивая девятый и первый децили, измеряют соотношение уровней доходов 10% наиболее обеспеченного и 10% наименее обеспеченного населения (в разах). Формулы для определения децилей в интервальном ряду распределения имеют следующий вид:

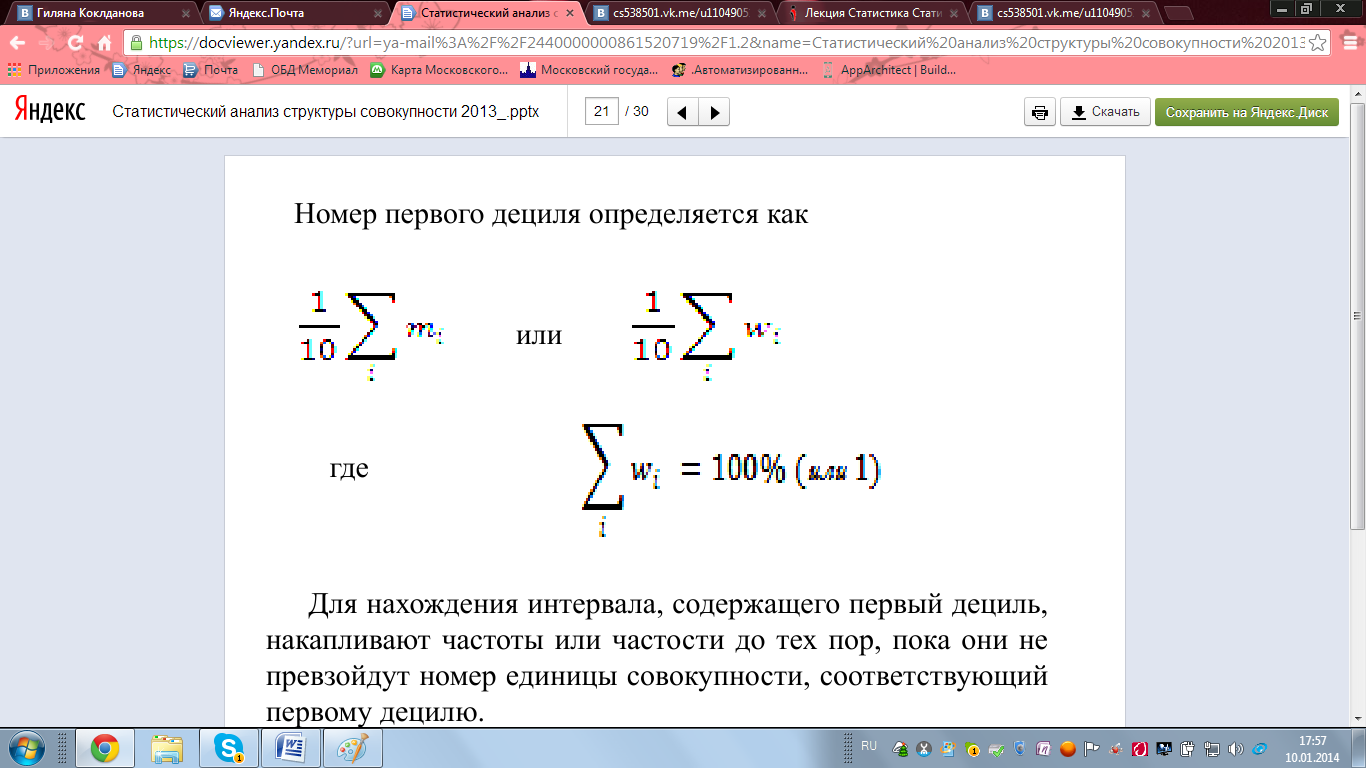
Где xk-1 – нижняя граница интервала, содержащего первый дециль,

hk = xk – xk-1 – длина интервала, содержащего первый дециль,

Fk-1 и pk-1 соответственно накопленные частоты и накопленные частости предшествующего интервала,

mk и wk – соответственно частота и частость интервала, содержащего первый дециль.

Номер первого дециля определяется как:

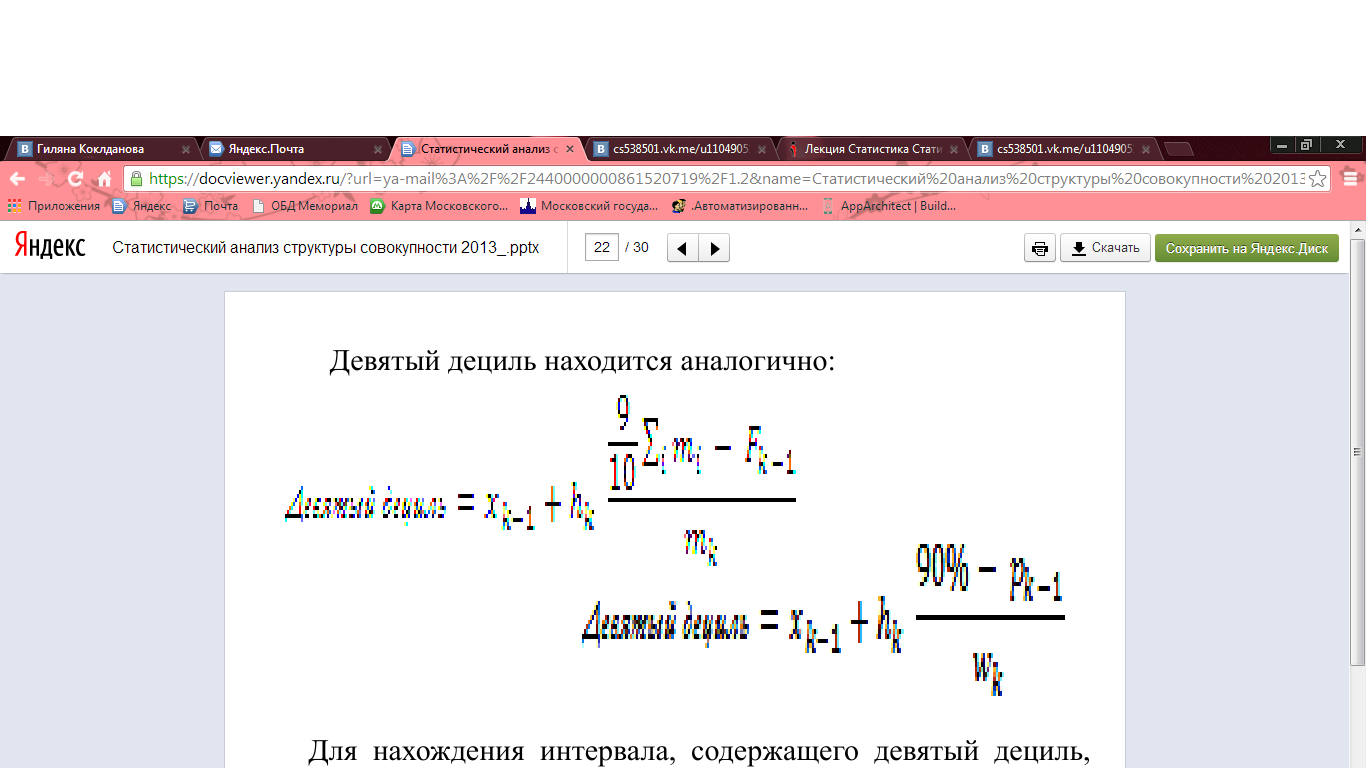
Для нахождения интервала, содержащего первый дециль, накапливают частоты или частости до тех пор, пока они не превзойдут номер единицы совокупности, соответствующий первому децилю.

Девятый дециль находится аналогично:

Для нахождения интервала, содержащего девятый дециль, частости накапливают до тех пор, пока они не превзойдут номер единицы совокупности, соответствующей девятому децилю, т.е. 90%.

3. Более точно уровень дифференциации можно измерить, сопоставив средние или суммарные величины активов 10% самых крупных и 10% самых мелких банков. Такой показатель называют фондовым коэффициентом Кф.