
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этапы развития статистики как науки. Ключевые особенности статистики как общественной науки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Этапы развития статистики как науки. Ключевые особенности статистики как общественной науки. Статистика — это сфера научной и практической деятельности, целью которой является получение, накопление, обработка, анализ и публикация сведений, позволяющих понять характер, тенденции и закономерности развития различных сфер общества (экономической, социальной, культурной и т. д.), а также общества в целом, на основе изучения и обобщения количественных закономерностей соответствующих данных в неразрывной связи с их качественным содержанием. В первую очередь статистика - общественная наука. Она дает количественную характеристику общественным явлениям и позволяет оценивать закономерности их развития. Информационной базой статистики служат эмпирические данные, получаемые на основе наблюдений массовых общественных явлений. Центральным звеном социального мира, который служит предметной областью статистики в её изначальном понимании, является человек. Предмет познания статистики обусловливает её специфические черты и особенности. Основные из них заключаются в следующем: 1. Статистика изучает только социально-экономические явления и процессы имеющие количественное выражение (население, труд, производство, распределение и потребление материальных благ, финансовые потоки, инфляцию и т.д.). 2. Статистика исследует не отдельные, а массовые общественные явления и процессы, рассматривая их как совокупности, состоящие из множества единичных элементов или фактов. Так, статистика изучает изменение производительности труда не одного конкретного работника, а совокупности работников на совокупности предприятий. 3. Для статистики цифры без их качественного содержания, без указания конкретного места и времени, к которым они относятся, лишены всякого смысла. Любой статистический показатель всегда выражает количественно-качественную характеристику явления. Статистика изучает количественные характеристики общественных явлений и процессов для того, чтобы на количественной основе познать качественное содержание, сущность явлений. 4. Изучая явления, статистика, прежде всего, характеризует его структуру, т.е. внутреннее строение, внутренние связи в объекте исследования – его составные части, их соотношение с объектом в целом и между собой. 5. Важным направлением статистики является изучение закономерностей изменения явлений. 6. Статистика, изучая связи между общественными явлениями, устанавливает круг основных факторов, влияющих на явление, измеряет силу влияния этих факторов.
Этапы развития науки 1. Первые учетные операции проводились еще в глубокой древности. За несколько тысячелетий до нашей эры в Китае, Индии, Египте проводились переписи населения. Вначале они были примитивны, нерегулярны (для войны). Аристотель составил описание 157 городов и государств своего времени. 2. В середине XIII в., когда Русь была завоевана монголами, монгольские ханы проводили переписи населения Руси для взимания дани с захваченных земель. 3. Развитие международной торговли вызвало необходимость иметь сведения не только о своей стране, но и о тех государствах, с которыми можно было торговать. Постепенно, главным образом в Германии, сформировалась школа описательного государствоведения. В России последователями «школы государствоведения» были Иван Кириллович Кирилов(1689-1737), Василий Никитич Татищев (1686-1750), Михаил Васильевич Ломоносов (1711-1765). 4. Как наука статистика начала своё становление в Англии во второй половине ХVII в. В работах представителей другой ветви предшественников статистической науки — так называемой школы политических арифметиков Джона Граунта и особенно Вильяма Петти впервые было показано, что статистика — не только собирание и регистрация сведений. Оказалось, что она позволяет с помощью специальных приёмов обработки собранного материала обнаружить важные закономерности и взаимозависимости между данными, которые дают возможность глубже понять смысл общественных явлений. Два направления: демографическое и социально-экономическое. Таким образом, статистика как наука сформировалась в результате синтеза государствоведения и политической арифметики. Если от государствоведения она унаследовала систему статистического описания социально-экономических явлений жизни государства, то от политической арифметики – количественный подход к анализу общественных явлений с целью познания их закономерностей. 5. Новый бурный этап развития статистики связывается с именем бельгийца А. Кетле который установил, что общественные явления, будучи внешне случайными, подчинены внутренним закономерностям. 6. Крупный русский статистик Д.П. Журавский показал значение предварительной структуризации (группировки, категоризации) статистических величин для понимания сущности изучаемых явлений и назвал саму статистику наукой категориального исчисления.
В качестве научного направления статистика начала развиваться в результате включения в свой теоретико-методологический арсенал идей и принципов естествознания. Творцы эмпирического обществознания заимствовали у естествоиспытателей подходы и критерии организации исследовательской деятельности, создавая новые (для них) формы научного мышления. Целью основоположников статистики было достижение ею статуса «точной», «позитивной» науки.
7. Стык XIX — ХХ вв. ознаменовался для статистики как науки об обществе заметным кризисом. Этот кризис разрешился выходом идей, концепций и методов статистики в другие сферы науки и социальной практики. Если её предметной сферой была только общественная жизнь, то в дальнейшем она всё более стала перемещаться в биологию (Гальтон), затем в физику (Гольцман) в технические науки и т.д. В частности, произошло соединение статистического метода с идеями теории вероятностей и математики вообще. Мало-помалу статистика превратилась в отрасль математики — прикладную теорию вероятностей. 8. Завершая короткий исторический экскурс развития статистических идей, заметим,что, оставаясь самостоятельной общественной наукой, статистика примерно в конце XIX в. дала толчок развитию одного из разделов математики — теории вероятностей. В рамках этого раздела развилось новое научное направление — математическая статистика. Будучи разделом математики, она стала непонятной и потому недоступной для статистика-обществоведа. Хотя и появилась довольно обильная соответствующая литература, читать и понимать ее мог только тот, кто свободно владел высшей математикой. Поэтому провести полноценный методологический анализ возможностей и ограничений этой новой математической статистики для ученого-гуманитария или предметника - обществоведа стало весьма затруднительно (к сожалению, и в настоящее время ситуация мало изменилась!).
Основные понятия статистики (статистическая совокупность, признаки, вариации признаков, статистический показатель). статистика - сфера научной и практической деятельности, целью которой является получение, накопление, обработка, анализ и публикация сведений, позволяющих понять характер, тенденции и закономерности развития различных сфер общества, а также общества в целом. статистика - общественная наука. Она дает количественную характеристику общественным явлениям и позволяет оценивать закономерности их развития. В рамках отраслевых статистик (промыш, сельскохоз, строительство, транспорт, связь) развивается социальная статистика. Статистические совокупности - изучаемые статистиком массовые явления в виде множества однокачественных единиц с отличающимися индивидуальными признаками. Пример: совокупность населения, промыш предприятий, совокупность работников, банков. Единица совокупности – множество, кот образует изучаемую стат совокупность. Каждая единица совокупности может быть охарактеризована разными качественными и количественными признаками. Признак - свойство, характерная черта явления, подлежащая статистическому изучению. Если опр признак имеет разные значения у отдельных единиц совокупности, то он имеет некоторую вариацию. Такие признаки, варьирующие от ед к единице, составляют отличит черту статистич совокупности. Присутствие вариации у единиц совокупности обозначает, что их признаки могут получать всевозможные значения или видоизменения у некоторых единиц совокупности. Зырянов: Признаки различаются способами их измерения и другими особенностями, влияющими на приемы статистического изучения: 1)По характеру выражения: 1.Описательные признаки (атрибутивные) выражаются словесно: национальность человека, разновидность почв, материал изделия. Описательные признаки подразделяются на: номинальные –описательные признаки, по которым нельзя ранжировать данные; порядковые – те, по которым можно ранжировать, упорядочивать данные. 2.Количественные признаки выражены числами. Они играют преобладающую роль в статистике. возраст человека, заработная плата рабочих, население города, доход кооператива и.т.д. 2)По способу измерения: 1.Первичные признаки хар-т единицу совокупности в целом. Это абсолютные величины. Они существуют сами по себе независимо от их статистического изучения. Они могут быть измерены, сосчитаны, взвешены. Таковы площадь пашни, мощность двигателей на предприятии. 2.Вторичные, или расчетные признаки не измеряются непосредственно, а рассчитываются. Вторичные признаки представляют собой соотношение первичных признаков: деление объема выпущенной продукции на численность работников дает показатель производительности труда. 3)По отношению к характеризуемому объекту: 1.Прямые (непосредственные) признаки - свойства, непосредственно присущие тому объекту, который ими характеризуется. возраст человека, объем продукции предприятия, численность его рабочих. 2.Косвенные признаки - свойства, присущие не самому объекту, а другим совокупностям, относящимся к объекту, входящим в него. 4)По характеру вариаций (т.е. по различиям их значений у разных единиц совокупности): 1.Альтернативные признаки могут принимать только два значения т.е. предмет может обладать или не обладать чем – либо. 2.Дискретные признаки - количественные признаки, которые могут иметь только отдельные значения. число студентов в группе, число аудиторий, число книг в библиотеке и т.д. 3.Непрерывные признаки способны принимать любые значения в определенных границах. К непрерывным относятся расчетные вторичные признаки. 5)По отношению ко времени: 1.Моментальные признаки характеризуют изучаемый объект в какой-то момент времени, установленный планом статистического исследования. 2.Интервальные признаки - признаки, характеризующие результаты процессов. число родившихся, умерших,, сумма полученной прибыли и т.д. Зырянов: Статистический показатель - понятие (категория) отображающее количественные характеристики (размеры) соотношения признаков общественных явлений. Статистические показатели могут быть объемными (численность населения, трудовых ресурсов) и расчетными (средние величины); плановыми, отчетными и прогностическими (т.е. выступать в качестве прогнозных оценок). Статистическиепоказатели следует отличать от статических данных. Статические данные -конкретные численные значения статистических показателей. Они определены нетолько качественно, но и количественно и зависят от конкретных условий места и времени. Любой статистический показатель отражает количественно-качественную характеристику явления, поэтому наряду с числовой величиной показателя в нем должно быть отражено: 1)явление измеряется показателем; 2)время (на определенную дату, на начало месяца, квартала, года), интервал времени; 3)обстоятельство места - отнесение показателя к конкретному объекту, отрасли экономики, территории; 4)единицы измерения, в которых выражается величина явления. Закономерность, выявленная на основе массового наблюдения - статистич закономерность.
Смыкание рядов динамики.
25. Показатели ряда динамики (абсолютный прирост, темп роста). 26. Показатели ряда динамики (темп прироста, абсолютное значение 1% прироста). Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения. Базисный темп прироста
Цепной темп прироста
Между показателями темпа прироста и темпа роста имеется взаимосвязь:
(при выражении роста в процентах)
Если уровни ряда динамики сокращаются, то соответствующие показатели темпа прироста будут со знаком минус, так как они характеризуют относительное уменьшение прироста уровня динамики.
Показатель абсолютного значения 1% прироста (λ) равен частному от деления абсолютного прироста на темп прироста:
А так как темп прироста равен частному от деления абсолютного прироста, умноженного на 100, на величину первоначального уровня, то абсолютное значение 1% прироста оказывается равно первоначальному уровню деленному на 100:
Про них в вопросе 43
Агрегатный (общий) индекс физического объема продукции
Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства.
Индекс показывает во сколько раз увеличилась (уменьшилась) стоимость продукции (товарооборот) отчетного периода по сравнению с базисным. Разность числителя и знаменателя Σp1q1 - Σp0q0 показывает, на сколько рублей (др. единиц) увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Если из значения индекса стоимости вычесть 100% (Ipq – 100), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в отчетном периоде по сравнению с базисным.
Индексы Пааше и Ласпейреса
Индекс Г. Пааше.
В качестве неизменного количества товара берется объем продукции отчетногопериода. Показывает, насколько товары в отчетном периоде стали дороже (дешевле), чем в базисном.
Индекс Э. Ласпейреса Индекс исчисляется по количествам базисного периода. Показывает, во сколько бы раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде Практика использования этих индексов показала, что индекс рассчитанный по формуле Пааше, имеет тенденцию некоторого занижения, а по формуле Ласпейреса – завышения темпов инфляции. Общее правило для индексов цен, себестоимости, производительности труда и подобных им заключается в том, что абсолютные суммы экономии (перерасхода) в отчетном периоде от снижения (повышения) цен (себестоимости, производительности труда) можно получить только на основе индексов цен рассчитанных на продукцию отчетного периода, т.е. индексов Пааше.
Индекс различий
где di1 di0 — удельные веса отдельных элементов двух сравниваемых совокупностей; Индекс различий, рассчитанный через удельные веса, выраженные в процентах, может принимать значения от 0 до 100%, приближение к нулю означает отсутствие изменений, приближение к максимуму — свидетельство значительного изменения структуры. Коэффициент структурных сдвигов К. Гатева
Приведенные выше показатели не дают представления об изменениях удельных весов отдельных элементов совокупности. Данный показатель учитывает интенсивность изменений по отдельным группам в сравниваемых структурах. Количество групп, на которое поделена исследуемая совокупность, влияет на итоговую оценку структурных изменений. Индекс Рябцева
Значения этого показателя не зависят от числа градаций структур. Оценка производится на основе максимально возможной величины расхождений между компонентами структуры, происходит соотношение фактических расхождений отдельных компонентов структур с максимально возможными значениями. Данный коэффициент (индекс) также принимает значения от нуля до единицы. Преимуществом данного показателя может считаться и наличие шкалы оценки полученных значений показателя. Приведённые показатели представляют характеристику структурных изменений, но не дают представления о величине этих изменений. Для количественной оценки степени неравномерности используются два коэффициента концентрации доходов — Лоренца и Джини. Коэффициент Лоренца
где yi — доля доходов i-й группы; хi — доля населения i -й группы.
Расчет коэффициента Джини основан на определении доли площади многоугольника, очерченного диагональю квадрата и кривой Лоренца, в половине площади квадрата:
где cum yi — накопленные доли доходов
Оба коэффициента изменяются в пределах от 0 до 1. Чем ближе значение к 1, тем выше уровень неравенства (концентрации) в распределении доходов. Предельных значений данные коэффициенты на практике не достигают (0 — полное равенство, 1 — концентрация доходов у одной группы населения). При расчете и сравнении значений коэффициента Джини следует обращать внимание на то, по каким группировкам рассчитан показатель, так как чем на большее число групп разделена анализируемая совокупность, тем выше будет значение коэффициента Джини. Например, коэффициент, рассчитанный по 10%-ным группам, всегда будет выше коэффициента, рассчитанного по 20%-ным группам. Теория Парето — Лоренца — Джини была предложена для изучения равномерности или неравномерности (концентрации) распределения совокупных доходов среди всех групп населения. Однако, эти коэффициенты могут быть использованы при изучении степени равномерности распределения других социальных и экономических признаков. Например, степени равномерности распределения жилья, социальных трансфертов, медицинских и образовательных услуг, преступности и др. При оценке степени монополизации отрасли используется коэффициент Герфиндаля
где di — удельный вес i-го предприятия; k — число предприятий в отрасли. Вычисление коэффициента производится через сумму квадратов долей продаж каждого предприятия отрасли, выраженных в процентах. Следовательно, максимальное значение коэффициента Герфиндаля может составлять 10000, минимальное - 10000 /k. Коэффициент Лоренца
где yi — доля доходов i-й группы; хi — доля населения i -й группы.
Расчет коэффициента Джини основан на определении доли площади многоугольника, очерченного диагональю квадрата и кривой Лоренца, в половине площади квадрата:
где cum yi — накопленные доли доходов
Оба коэффициента изменяются в пределах от 0 до 1. Чем ближе значение к 1, тем выше уровень неравенства (концентрации) в распределении доходов. Предельных значений данные коэффициенты на практике не достигают (0 — полное равенство, 1 — концентрация доходов у одной группы населения). При расчете и сравнении значений коэффициента Джини следует обращать внимание на то, по каким группировкам рассчитан показатель, так как чем на большее число групп разделена анализируемая совокупность, тем выше будет значение коэффициента Джини. Например, коэффициент, рассчитанный по 10%-ным группам, всегда будет выше коэффициента, рассчитанного по 20%-ным группам. Теория Парето — Лоренца — Джини была предложена для изучения равномерности или неравномерности (концентрации) распределения совокупных доходов среди всех групп населения. Однако, эти коэффициенты могут быть использованы при изучении степени равномерности распределения других социальных и экономических признаков. Например, степени равномерности распределения жилья, социальных трансфертов, медицинских и образовательных услуг, преступности и др. Для измерения фактического распределения доходов используют «кривую Лоренца» и «коэффициент Джини», показывающие, какая доля совокупного дохода приходится на каждую группу населения, что позволяет судить об уровне экономического неравенства в данной стране.
Коэффициент Лоренца
где yi — доля доходов i-й группы; хi — доля населения i -й группы. «Кривая Лоренца» — это метод графического изображения уровня концентрации явления. Для ее построения на обе оси координат наносят процентную масштабную шкалу (от 0 до 100 %). Для точек кривой абсциссами служат единицы совокупности, а ординатами — значения признака. Равномерное распределение признака будет представлено в таком случае диагональю, называемой «линией равномерного распределения», а неравномерное — «линией Лоренца», отклонение которой от диагонали и характеризует степень неравномерности (см. график 17.1).
Этапы развития статистики как науки. Ключевые особенности статистики как общественной науки. Статистика — это сфера научной и практической деятельности, целью которой является получение, накопление, обработка, анализ и публикация сведений, позволяющих понять характер, тенденции и закономерности развития различных сфер общества (экономической, социальной, культурной и т. д.), а также общества в целом, на основе изучения и обобщения количественных закономерностей соответствующих данных в неразрывной связи с их качественным содержанием. В первую очередь статистика - общественная наука. Она дает количественную характеристику общественным явлениям и позволяет оценивать закономерности их развития. Информационной базой статистики служат эмпирические данные, получаемые на основе наблюдений массовых общественных явлений. Центральным звеном социального мира, который служит предметной областью статистики в её изначальном понимании, является человек. Предмет познания статистики обусловливает её специфические черты и особенности. Основные из них заключаются в следующем: 1. Статистика изучает только социально-экономические явления и процессы имеющие количественное выражение (население, труд, производство, распределение и потребление материальных благ, финансовые потоки, инфляцию и т.д.). 2. Статистика исследует не отдельные, а массовые общественные явления и процессы, рассматривая их как совокупности, состоящие из множества единичных элементов или фактов. Так, статистика изучает изменение производительности труда не одного конкретного работника, а совокупности работников на совокупности предприятий. 3. Для статистики цифры без их качественного содержания, без указания конкретного места и времени, к которым они относятся, лишены всякого смысла. Любой статистический показатель всегда выражает количественно-качественную характеристику явления. Статистика изучает количественные характеристики общественных явлений и процессов для того, чтобы на количественной основе познать качественное содержание, сущность явлений. 4. Изучая явления, статистика, прежде всего, характеризует его структуру, т.е. внутреннее строение, внутренние связи в объекте исследования – его составные части, их соотношение с объектом в целом и между собой. 5. Важным направлением статистики является изучение закономерностей изменения явлений. 6. Статистика, изучая связи между общественными явлениями, устанавливает круг основных факторов, влияющих на явление, измеряет силу влияния этих факторов.
Этапы развития науки 1. Первые учетные операции проводились еще в глубокой древности. За несколько тысячелетий до нашей эры в Китае, Индии, Египте проводились переписи населения. Вначале они были примитивны, нерегулярны (для войны). Аристотель составил описание 157 городов и государств своего времени. 2. В середине XIII в., когда Русь была завоевана монголами, монгольские ханы проводили переписи населения Руси для взимания дани с захваченных земель. 3. Развитие международной торговли вызвало необходимость иметь сведения не только о своей стране, но и о тех государствах, с которыми можно было торговать. Постепенно, главным образом в Германии, сформировалась школа описательного государствоведения. В России последователями «школы государствоведения» были Иван Кириллович Кирилов(1689-1737), Василий Никитич Татищев (1686-1750), Михаил Васильевич Ломоносов (1711-1765). 4. Как наука статистика начала своё становление в Англии во второй половине ХVII в. В работах представителей другой ветви предшественников статистической науки — так называемой школы политических арифметиков Джона Граунта и особенно Вильяма Петти впервые было показано, что статистика — не только собирание и регистрация сведений. Оказалось, что она позволяет с помощью специальных приёмов обработки собранного материала обнаружить важные закономерности и взаимозависимости между данными, которые дают возможность глубже понять смысл общественных явлений. Два направления: демографическое и социально-экономическое. Таким образом, статистика как наука сформировалась в результате синтеза государствоведения и политической арифметики. Если от государствоведения она унаследовала систему статистического описания социально-экономических явлений жизни государства, то от политической арифметики – количественный подход к анализу общественных явлений с целью познания их закономерностей. 5. Новый бурный этап развития статистики связывается с именем бельгийца А. Кетле который установил, что общественные явления, будучи внешне случайными, подчинены внутренним закономерностям. 6. Крупный русский статистик Д.П. Журавский показал значение предварительной структуризации (группировки, категоризации) статистических величин для понимания сущности изучаемых явлений и назвал саму статистику наукой категориального исчисления.
В качестве научного направления статистика начала развиваться в результате включения в свой теоретико-методологический арсенал идей и принципов естествознания. Творцы эмпирического обществознания заимствовали у естествоиспытателей подходы и критерии организации исследовательской деятельности, создавая новые (для них) формы научного мышления. Целью основоположников статистики было достижение ею статуса «точной», «позитивной» науки.
7. Стык XIX — ХХ вв. ознаменовался для статистики как науки об обществе заметным кризисом. Этот кризис разрешился выходом идей, концепций и методов статистики в другие сферы науки и социальной практики. Если её предметной сферой была только общественная жизнь, то в дальнейшем она всё более стала перемещаться в биологию (Гальтон), затем в физику (Гольцман) в технические науки и т.д. В частности, произошло соединение статистического метода с идеями теории вероятностей и математики вообще. Мало-помалу статистика превратилась в отрасль математики — прикладную теорию вероятностей. 8. Завершая короткий исторический экскурс развития статистических идей, заметим,что, оставаясь самостоятельной общественной наукой, статистика примерно в конце XIX в. дала толчок развитию одного из разделов математики — теории вероятностей. В рамках этого раздела развилось новое научное направление — математическая статистика. Будучи разделом математики, она стала непонятной и потому недоступной для статистика-обществоведа. Хотя и появилась довольно обильная соответствующая литература, читать и понимать ее мог только тот, кто свободно владел высшей математикой. Поэтому провести полноценный методологический анализ возможностей и ограничений этой новой математической статистики для ученого-гуманитария или предметника - обществоведа стало весьма затруднительно (к сожалению, и в настоящее время ситуация мало изменилась!).
Основные понятия статистики (статистическая совокупность, признаки, вариации признаков, статистический показатель). статистика - сфера научной и практической деятельности, целью которой является получение, накопление, обработка, анализ и публикация сведений, позволяющих понять характер, тенденции и закономерности развития различных сфер общества, а также общества в целом. статистика - общественная наука. Она дает количественную характеристику общественным явлениям и позволяет оценивать закономерности их развития. В рамках отраслевых статистик (промыш, сельскохоз, строительство, транспорт, связь) развивается социальная статистика. Статистические совокупности - изучаемые статистиком массовые явления в виде множества однокачественных единиц с отличающимися индивидуальными признаками. Пример: совокупность населения, промыш предприятий, совокупность работников, банков. Единица совокупности – множество, кот образует изучаемую стат совокупность. Каждая единица совокупности может быть охарактеризована разными качественными и количественными признаками. Признак - свойство, характерная черта явления, подлежащая статистическому изучению. Если опр признак имеет разные значения у отдельных единиц совокупности, то он имеет некоторую вариацию. Такие признаки, варьирующие от ед к единице, составляют отличит черту статистич совокупности. Присутствие вариации у единиц совокупности обозначает, что их признаки могут получать всевозможные значения или видоизменения у некоторых единиц совокупности. Зырянов: Признаки различаются способами их измерения и другими особенностями, влияющими на приемы статистического изучения: 1)По характеру выражения: 1.Описательные признаки (атрибутивные) выражаются словесно: национальность человека, разновидность почв, материал изделия. Описательные признаки подразделяются на: номинальные –описательные признаки, по которым нельзя ранжировать данные; порядковые – те, по которым можно ранжировать, упорядочивать данные. 2.Количественные признаки выражены числами. Они играют преобладающую роль в статистике. возраст человека, заработная плата рабочих, население города, доход кооператива и.т.д. 2)По способу измерения: 1.Первичные признаки хар-т единицу совокупности в целом. Это абсолютные величины. Они существуют сами по себе независимо от их статистического изучения. Они могут быть измерены, сосчитаны, взвешены. Таковы площадь пашни, мощность двигателей на предприятии. 2.Вторичные, или расчетные признаки не измеряются непосредственно, а рассчитываются. Вторичные признаки представляют собой соотношение первичных признаков: деление объема выпущенной продукции на численность работников дает показатель производительности труда. 3)По отношению к характеризуемому объекту: 1.Прямые (непосредственные) признаки - свойства, непосредственно присущие тому объекту, который ими характеризуется. возраст человека, объем продукции предприятия, численность его рабочих. 2.Косвенные признаки - свойства, присущие не самому объекту, а другим совокупностям, относящимся к объекту, входящим в него. 4)По характеру вариаций (т.е. по различиям их значений у разных единиц совокупности): 1.Альтернативные признаки могут принимать только два значения т.е. предмет может обладать или не обладать чем – либо. 2.Дискретные признаки - количественные признаки, которые могут иметь только отдельные значения. число студентов в группе, число аудиторий, число книг в библиотеке и т.д. 3.Непрерывные признаки способны принимать любые значения в определенных границах. К непрерывным относятся расчетные вторичные признаки. 5)По отношению ко времени: 1.Моментальные признаки характеризуют изучаемый объект в какой-то момент времени, установл
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 2389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.252 (0.015 с.) |

 вычисляется делением сравниваемого базисного абсолютного прироста
вычисляется делением сравниваемого базисного абсолютного прироста  на уровень, принятый за постоянную базу сравнения
на уровень, принятый за постоянную базу сравнения  :
:
 – это отношение сравниваемого цепного абсолютного прироста
– это отношение сравниваемого цепного абсолютного прироста  к предыдущему уровню
к предыдущему уровню  :
:



 Индивидуальный индекс физического объема продукции показывает во сколько раз возрос (уменьшился) выпуск какого либо одного товара в отчетном периоде по сравнению с базисным:
Индивидуальный индекс физического объема продукции показывает во сколько раз возрос (уменьшился) выпуск какого либо одного товара в отчетном периоде по сравнению с базисным:
 Индекс товарооборота (стоимости продукции) представляет собой отношение стоимости продукции текущего периода (Σp1q1) к стоимости продукции в базисном периоде (Σp0q0) и определяется по формуле:
Индекс товарооборота (стоимости продукции) представляет собой отношение стоимости продукции текущего периода (Σp1q1) к стоимости продукции в базисном периоде (Σp0q0) и определяется по формуле: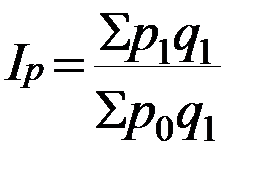
 Агрегатный индекс цен показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен.
Агрегатный индекс цен показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен.
 Пытаясь преодолеть недостатки индексов Пааше и Ласпейреса американский экономист И. Фишер предложил свой вариант индекса цен.
Пытаясь преодолеть недостатки индексов Пааше и Ласпейреса американский экономист И. Фишер предложил свой вариант индекса цен.






 Таким образом, если принять величину дохода и численность населения за 100 %, то прямая ОА покажет абсолютно равномерное распределение совокупного дохода между всеми группами населения. Однако реальное распределение всегда будет характеризоваться отклонением от этой прямой. Абсолютно неравномерное распределение совпало бы с осями координат. Но поскольку «сверхбедные» и «сверхбогатые» всегда составляют незначительную часть рыночного общества, то перед нами будет некоторая кривая («кривая Лоренца»), отклонение которой от диагонали наглядно покажет степень неравномерного распределения доходов.
Таким образом, если принять величину дохода и численность населения за 100 %, то прямая ОА покажет абсолютно равномерное распределение совокупного дохода между всеми группами населения. Однако реальное распределение всегда будет характеризоваться отклонением от этой прямой. Абсолютно неравномерное распределение совпало бы с осями координат. Но поскольку «сверхбедные» и «сверхбогатые» всегда составляют незначительную часть рыночного общества, то перед нами будет некоторая кривая («кривая Лоренца»), отклонение которой от диагонали наглядно покажет степень неравномерного распределения доходов.


