
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютные и относительные показатели изменения структур. Структурные сдвиги и структурные различия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сравнение двух одноименных структур в пространстве проводится при помощи абсолютных показателей различий и коэффициентов абсолютных сдвигов. Они могут быть подсчитаны при разном количестве элементов у сравниваемых структур. Изменения удельных весов одной и той же структуры во времени измеряются относительными показателями различий и коэффициентами относительных структурных сдвигов. Подсчитываются только в том случае, если количество элементов в структурах одинаково. Показатели, характеризующие не изменение отдельной доли, а изменение структуры в целом, - т. е.«структурный сдвиг». Движение системы во времени, носящее управляемый характер, мы считаем трансформацией. Для измерения силы и глубины трансформации, проявляющейся в структурных сдвигах, в статистике используются специальные методы, рассчитываются специфические показатели. В условиях измерения абсолютных структурных сдвигов классическая формула среднего линейного отклонения трансформируется в следующую:
где Этот показатель Л.С. Казинец назвал линейным коэффициентом абсолютных структурных сдвигов. Статистически его смысл состоит в том, что он представляет собой среднюю арифметическую из модулей абсолютных приростов долей (удельных весов) всех частей сравниваемых целых. Данный коэффициент характеризует среднюю величину отклонений от удельных весов, то есть показывает, на сколько процентных пунктов в среднем отклоняются друг от друга удельные веса частей в сравниваемых совокупностях. Чем больше величина линейного коэффициента абсолютных структурных сдвигов, тем больше в среднем отклоняются друг от друга удельные веса отдельных частей за два сравниваемых периода, тем сильнее абсолютные структурные сдвиги. Если структуры за эти периоды совпадают (т.е. d 2 - d 1 = 0), то данный коэффициент будет равен нулю. Индекс различий
где di1 di0 — удельные веса отдельных элементов двух сравниваемых совокупностей; Индекс различий, рассчитанный через удельные веса, выраженные в процентах, может принимать значения от 0 до 100%, приближение к нулю означает отсутствие изменений, приближение к максимуму — свидетельство значительного изменения структуры. Коэффициент структурных сдвигов К. Гатева
Приведенные выше показатели не дают представления об изменениях удельных весов отдельных элементов совокупности. Данный показатель учитывает интенсивность изменений по отдельным группам в сравниваемых структурах. Количество групп, на которое поделена исследуемая совокупность, влияет на итоговую оценку структурных изменений. Индекс структурных различий Салаи. Данный показатель учитывает также число групп или элементов в сравниваемых структурах. Коэффициент (индекс) Салаи, как и коэффициент К. Гатева могут принимать значения от нуля до единицы. Чем ближе полученное значение к единице, тем существеннее произошедшие структурные изменения. Коэффициент Салаи принимает близкие к единице значения, когда в сумме большое количество единиц. Индекс Рябцева
Значения этого показателя не зависят от числа градаций структур. Оценка производится на основе максимально возможной величины расхождений между компонентами структуры, происходит соотношение фактических расхождений отдельных компонентов структур с максимально возможными значениями. Данный коэффициент (индекс) также принимает значения от нуля до единицы. Преимуществом данного показателя может считаться и наличие шкалы оценки полученных значений показателя. Приведённые показатели представляют характеристику структурных изменений, но не дают представления о величине этих изменений. Для количественной оценки степени неравномерности используются два коэффициента концентрации доходов — Лоренца и Джини. Коэффициент Лоренца
где yi — доля доходов i-й группы; хi — доля населения i -й группы.
Расчет коэффициента Джини основан на определении доли площади многоугольника, очерченного диагональю квадрата и кривой Лоренца, в половине площади квадрата:
где cum yi — накопленные доли доходов
Оба коэффициента изменяются в пределах от 0 до 1. Чем ближе значение к 1, тем выше уровень неравенства (концентрации) в распределении доходов. Предельных значений данные коэффициенты на практике не достигают (0 — полное равенство, 1 — концентрация доходов у одной группы населения). При расчете и сравнении значений коэффициента Джини следует обращать внимание на то, по каким группировкам рассчитан показатель, так как чем на большее число групп разделена анализируемая совокупность, тем выше будет значение коэффициента Джини. Например, коэффициент, рассчитанный по 10%-ным группам, всегда будет выше коэффициента, рассчитанного по 20%-ным группам. Теория Парето — Лоренца — Джини была предложена для изучения равномерности или неравномерности (концентрации) распределения совокупных доходов среди всех групп населения. Однако, эти коэффициенты могут быть использованы при изучении степени равномерности распределения других социальных и экономических признаков. Например, степени равномерности распределения жилья, социальных трансфертов, медицинских и образовательных услуг, преступности и др. При оценке степени монополизации отрасли используется коэффициент Герфиндаля
где di — удельный вес i-го предприятия; k — число предприятий в отрасли. Вычисление коэффициента производится через сумму квадратов долей продаж каждого предприятия отрасли, выраженных в процентах. Следовательно, максимальное значение коэффициента Герфиндаля может составлять 10000, минимальное - 10000 /k.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 10511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.78.65 (0.008 с.) |

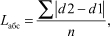 (1)
(1) - модуль абсолютного прироста долей (удельных весов) в текущем периоде по сравнению с базисным; n - число градаций.
- модуль абсолютного прироста долей (удельных весов) в текущем периоде по сравнению с базисным; n - число градаций.









