
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметры работ сетевого графика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проверим правильность табличных расчётов: L кр = (1-3-4-5-6) → т.к. на критическом пути лежат начальные события 1,3,4,5,6, то должно выполняться равенство R П(1,2) = R 1(1,2); R П(1,3) = = R 1(1,3); R П(3,4) = R 1(3,4); R П(4,5) = R 1(4,5); R П(4,6) = R 1(4,6); R П(5,6) = R 1(5,6). Если на критическом пути лежит конечное событие, то должно выполняться равенство R П(1,3) = R с(1,3); R П(2,5) = R с(2,5); R П(2,3) = R с(2,3); R П(3,4)= = R с(3,4); R П(4,5) = R с(4,5); R П(4,6) = R с(4,6); R П(5,6) = R с(5,6). Если на критическом пути лежат начальное и конечное события, то выполняется следующее равенство: R П(1,3) = R 1(1,3) = R с(1,3) = R н(1,3); R П(3,4) = R 1(3,4) = R с(3,4) = R н(3,4); R П(4,5) = R 1(4,5) = R с(4,5) = R н(4,5); R П(5,6) = R 1(5,6) = R с(5,6) = R н(5,6). В представленном примере все перечисленные условия выполняются, следовательно, расчёты произведены правильно. Для небольших проектов удобным дополнением к сетевому графику является линейный график или график Ганта. (рис.3.8).
На линейном графике каждая работа (i,j) изображается в привязке к оси времени 0t горизонтальным отрезком, длина которого в соответствующем масштабе равна продолжительности работы tij. Начало каждой работы совпадает с ранним сроком свершения её начального события. Работы изображаются в той же последовательности, что и на сети.
Анализ сетевой модели Анализ сетевого графика, опирающийся на результаты расчетов, включает оценку целесообразности структуры графика, загрузки исполнителей работ на всех этапах выполнения проекта, возможности смещения начала работ некритической зоны и, наконец, оценку вероятности наступления события в заданный срок. Одним из первых шагов анализа построенного графика является пересмотр топологии сети, который заключается не только в контроле правильности построения графика, но и в установлении целесообразности детализации работ и структуры сети. При этом наряду с установлением лишних работ и проверкой целесообразности установленного уровня детализации должен быть рассмотрен вопрос возможности параллельного выполнения работ, исходя из особенностей планируемого процесса и имеющегося количества работников. Вторым этапом анализа может быть классификация и группирование работ по величинам резервов (полных и свободных). При этом следует подчеркнуть, что далеко не всегда величина полного резерва может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритической зоны. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова величина (протяженность) этой последовательности. Иными словами, важно не только абсолютное, но и относительное значение резерва работы или отрезка пути. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициентов напряженности работ. Коэффициент напряженности работ – это отношение продолжительности отрезка наибольшего из некритических путей, проходящего через данную работу, к продолжительности несовпадающего отрезка критического пути, проходящего через эту работу. Если совпадающую с критическим путем величину отрезка пути обозначить как t, (L кр ), длину критического пути – t(L кр ), а протяженность максимального из некритических путей, проходящего через данную работу, – t(L max ), то коэффициент напряженности работ К Формулу можно выразить через резерв времени: КН Чем выше коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. И наоборот, чем меньше коэффициент напряженности, тем большими относительными резервами обладает данный путь в сети. Расчет коэффициентов напряженности позволяет заново проанализировать топологию сети в отношении выравнивания коэффициентов напряженности путей. По полученным таким образом коэффициентам напряженности все работы распределяются по зонам: критическая, подкритическая и резервная. Критическая зона сетевого графика – это совокупность путей, включая критический, абсолютные значения резервов времени которых меньше заданной величины, то есть Кн ij, близкие к единице. Резервная зона – это совокупность работ, имеющих значение Кн ij значительно меньше единицы. Следующим этапом анализа является расчет вероятностных характеристик сетевых моделей. Расчет вероятности наступления завершающего события в заданный срок оказывается особенно необходимым, когда установленный директивный срок Т Д оказывается меньше расчетного срока Т К. Если предположить, что срок окончания работ является случайной нормально распределенной величиной, то вероятность выполнения работ в директивный срок определяется по формуле Р(Т≥ТД)= Ф (и)= Ф
Вначале определяем значение u, а затем по таблице приложения 4 функции Лапласа – вероятность выполнения работ в директивный срок. Здесь Для величины Р(Т ≥ Т Д ) устанавливаются вполне определенные пределы, именуемые границами допустимого риска. По данным практики выполнения работ по графикам, при Р(Т ≥ Т Д ) > 0,65 можно утверждать, что на работах критического пути имеются избыточные ресурсы, следовательно, общая продолжительность работ может быть сокращена. При Р(Т ≥ Т Д ) < 0,35 опасность срыва заданного срока выполнения работ очень велика и необходимо повторное планирование с перераспределением ресурсов. Оптимизация сетевого графика представляет собой процесс по улучшению организации выполнения комплекса работ с учетом установленного срока и использования ресурсов. Она осуществляется за счет: а) перераспределения ресурсов как временных, так и других; б) интенсификация выполнения работ критического пути; в) изменений в характере комплекса работ. При минимизации времени выполнения работ общий срок выполнения следует сокращать в первую очередь за счет изменения продолжительности критических работ. Выделение дополнительных ресурсов для критических работ, естественно, представляется более привлекательным, чем их интенсификация. Отработанная сетевая модель выполнения работ далее может быть преобразована в календарный график.
Задачи оптимизации на сетях Сетевые оптимизационные модели обычно являются частными случаями моделей линейного программирования. Чаще всего они используются в задачах распределения и расписаний. Модели этого класса имеют экономический смысл для хозяйственной деятельности. Достоинством сетей является то, что они идентичны структуре реальных операционных процессов. Кроме того, математическая структура сетей хорошо описывает операционные модели. Это и определяет широкое применение сетевых моделей. Рассмотрим некоторые из них. Модель транспортной задачи является одним из примеров оптимизации на линейных сетях. Она имеет вид: максимизировать
при ограничениях
xij= 1, j= Мы рассмотрели решение этой задачи симплекс-методом (методом потенциалов). Однако модель рассмотрена для одного продукта. Для многопродуктных задач спрос на всю номенклатуру продуктов необходимо привести к агрегированному продукту (например, все продукты выразить в тоннах) и к условной стоимости cij. Кроме того, канал поставки может быть с ограничением на объем перевозок xij огр, то есть канал имеет определенную пропускную способность, так что xij < xij огр. Такая модель называется ограниченной по пропускной способности. В некоторых задачах величина si – наличные ресурсы – является переменной. При таких условиях транспортная модель оказывается частным случаем более общей задачи линейного программирования. Другое важное обобщение классической транспортной задачи связано с учетом возможностей доставки ресурсов от поставщика i к потребителю j по маршруту, проходящему через промежуточный пункт. Этот случай часто возникает в системе товародвижения от предприятия к оптовому покупателю и далее к потребителю. Модель назначений можно кратко сформулировать следующим образом. Задано n работ, каждую из которых может выполнить любой из m исполнителей. Стоимость выполнения работы i исполнителем j равна cij. Нужно распределить исполнителей по работам, то есть назначить одного исполнителя на каждую работу, таким образом, чтобы минимизировать общие затраты. Математическая модель будет выглядеть следующим образом:
минимизировать
при ограничениях
xij= 0 при 1 для всех i и j. Отметим, что модель назначений является частным случаем классической транспортной задачи, в которой si=D= 1. Модель выбора критического пути объясняется следующим образом. Пусть задана сеть, каждой дуге которой соответствует некоторое расстояние. Нужно найти кратчайший путь в заданный узел из любого другого узла сети. Математическая постановка задачи имеет следующий вид: минимизировать
при ограничениях
где cij может быть расстоянием от с, или стоимостью переезда из узла i в узел j; источник – начальный узел, сток – конечный узел пути. Задача коммивояжера относится к ситуации: агент по сбыту собирается посетить каждый из городов п по одному разу, выехав из города i и вернувшись в него же. Расстояние между городами i и j равно cij. Каков кратчайший путь агента? Пример: Минимизировать
при ограничениях
где xij – неотрицательные целые решения при всех i и j, решение есть цикл. Полученное решение может содержать два и более несвязанных цикла. То есть можно получить, например, два независимых маршрута, один из которых проходит через города 1, 2,..., 3, а другой – через 4, 5,..., п. Требование о том, чтобы решение давало один цикл, значительно усложняет эту задачу, которая является комбинаторной. Задача планирования трудовых ресурсов возникает, когда требуется заключить контракт на выполнение определенного объема работ. Для построения математической модели, с помощью которой можно получить оптимальный план выполнения работ от начала 1 до конца п, обозначим: xij – число бригад, приступающих к работе в начале периода i и заканчивающих работу в начале периода j (где 1 cij Примем далее, что Rk – число бригад, действительно требующихся для выполнения заданного объема работ в течение периода k, где k= При этих условиях ограничения задачи выражаются следующим образом:
Минимизация целевой функции имеет вид:
В заключение следует отметить, что для успешного применения метода линейной оптимизации необходимо понимать основные математические идеи, заложенные в алгоритмах отыскания оптимального решения. Размерность реальных сетевых моделей настолько велика, что нетворческое применение линейной оптимизации для решения соответствующих задач крайне нерационально. В то же время использование особой структуры сетевых задач позволяет значительно сократить объем требующихся для получения решения вычислений.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1056; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.229.217 (0.007 с.) |



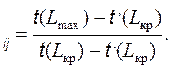

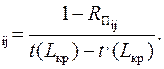
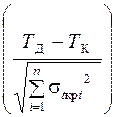 .
.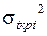 – дисперсия i -й работы критического пути; п – число работ критического пути.
– дисперсия i -й работы критического пути; п – число работ критического пути.
 j=
j= 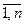 (спрос),
(спрос), i=
i= 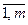 (наличные ресурсы),
(наличные ресурсы),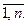



 i=
i= 
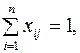 j=
j= 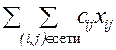
 для всех (i, j)
для всех (i, j)  сети,
сети,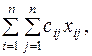 где
где 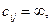 i=
i= 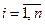 (отъезд),
(отъезд),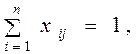 j=
j= 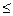 i < j
i < j 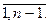

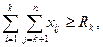 k=
k= 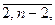
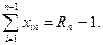
 min.
min.


