Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Временные параметры работ сетевого графикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Резервами времени располагают не только события, но и пути (кроме критического), а также работы, лежащие на некритическом пути. Для определения полного резерва времени пути R(Li) следует опять вернуться к тому условию, что длина критического пути в сетевом графике больше, чем длина любого другого пути. Разница между временем критического пути t(L кр ) и временем любого пути t(Li) называется полным резервом времени пути – R(Li) = t(L кр ) – t(L i ). Полный резерв пути показывает, на сколько могут быть увеличены продолжительности всех работ, принадлежащих пути Li, в сумме (предельное допустимое увеличение продолжительности пути). Существует четыре разновидности резервов времени работ. 1. Полный резерв времени работы – это максимальное количество времени, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительность критического пути. Полный резерв времени работы рассчитывается по формуле: RП (i,j) = Т п j – Т р j – tij, где i – начальное событие данной работы; j – конечное событие данной работы; tij – продолжительность работы от i -го до j -го события. 2. Частный резерв времени первого вида R 1(i,j) работы (i,j) есть часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока её начального события. Этим резервом можно располагать при выполнении данной работы в предположении, что её начальное и конечное событие свершаются в свои самые поздние сроки. Поэтому R1(i,j) вычисляется по формуле: R 1 (i,j) = Т п j – Т п i – tij = R П (i,j) – Ri, 3. Частный резерв времени второго вида, или свободный резерв времени R с (i,j) работы (i,j) представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока её конечного события. Этим резервом можно располагать при выполнении работы (i,j) в предположении, что её начальное и конечное событие события свершаются в свои самые ранние сроки: R с(i,j)= Т р j – Т р i – tij = R П (i,j) – Rj, 4. Независимый резерв времени R н(i,j) работы (i,j) – это часть полного резерва времени, соответствующая случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки: R н(i,j)= Т р j – Т п i – tij = R П (i,j) – Ri – Rj. Если на критическом пути лежит начальное событие i, то R П(i,j) = R 1(i,j). Если на критическом пути лежит конечное событие j, то R П(i,j) = R с (i,j). Если для данной работы R П(i,j) = R 1(i,j) = R С(i,j) = R Н(i,j), то данная работа лежит на критическом пути.
Пример. Проект включает в себя следующие работы (табл.3.3). Построить сетевой график выполнения комплекса работ. Рассчитать временные параметры событий и работ. Таблица 3.3 Параметры сетевого графика
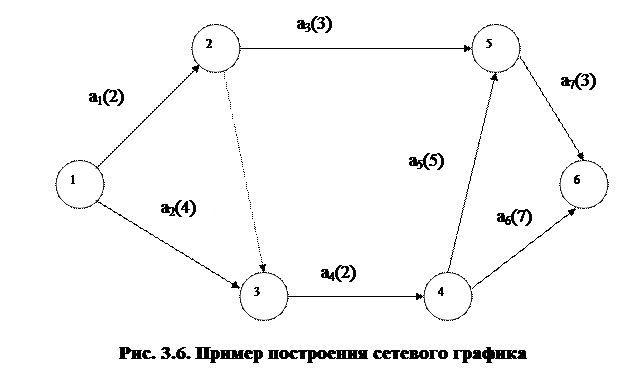
Решение: Исходное событие (1) означает момент начала выполнения проекта (рис.3.6). Работам а1 и а2 не предшествуют никакие работы, следовательно, на графике они изображены векторами, выходящими из исходного события. Работе а3 предшествует работа а1 , поэтому на графике дуга а3 непосредственно следует за дугой а1 . Событие (2) означает момент окончания работы а1 и начала работ, которым она предшествует. Работе а4 предшествуют работы а1 и а2. На графике эта зависимость отражена с помощью введения фиктивной работы (2,3). Моментом свершения события (3) будет момент, к которому будут выполнены работы а1 и а2 и может начинаться работа а4. Аналогично с учётом взаимосвязей изображаются на графике (рис. 3.6) все оставшиеся работы. Завершающее событие (6) означает момент выполнения всего проекта.
Замечание. Сетевая модель может быть задана в различной форме. Например, тот же самый проект может быть представлен следующим образом:
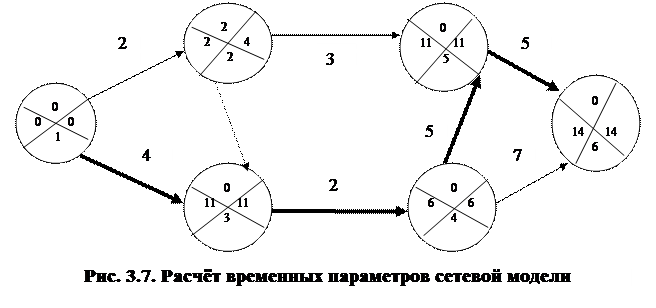
Расчёт основных временных параметров производится по соответствующим формулам, приведённым выше. Существует множество методов расчёта, в данном пособии рассматривается метод динамического программирования. Для нашего примера получим следующие результаты временных параметров событий сетевой модели: а ) ранние сроки свершения событий: Тр 1= 0; Тр 2 = Тр 1 + t 1,2 = 0 + 2 = 2; Тр 3 = max { Тр 1 + t 1,3; Тр 2 + t 2,3}= max{0 + 4; 2 + 0} = 4; Тр 4 = Тр 3 + t 3,4 = 4 +2 = 6; Тр 5 = max { Тр 2 + t 2,5; Тр 4 + t 4,5}= max{2 + 3; 6 + 5} = 11; Тр 6 = max { Тр 4 + t 4,6; Тр 5 + t 5,6}= max{6 + 7; 11 + 3} = 14. Итак, завершающее 6-е событие может свершиться лишь на 14-й день от начала разработки. Это минимальное время, за которое могут быть выполнены все работы проекта, оно определяется самым длинным полным путём. Ранний срок свершения события (6) Тр 6 = 14 совпадает с критическим временем t кр (суммарной продолжительностью работ, лежащих на критическом пути). Теперь можно выделить работы, принадлежащие критическому пути, возвращаясь от завершающего события к исходному. Из двух работ, входящих в событие (6), t кр = 14 определила работа (5,6), так как (Тр 5+ t 5,6 = 14), поэтому работа (5,6) является критической. Момент свершения события (5) определила работа (4,5), так как (Тр 4+ t 4,5 = 11), в связи с чем работа (4,5) будет критической. В свою очередь момент свершения события (4) определила работа (3,4), события (3) – работа (1,3). Все эти работы определили критический путь на сетевом графике: (1,3), (3,4), (4,5), (5,6). Условимся записывать это короче L кр = (1-3-4-5-6) (рис.3.7).
б) поздние сроки свершения событий: Т п6 = t кр. Воспользуемся снова методом динамического программирования, только расчёты будем вести с конца. Т п6 = 14, тогда Т п5 = 14 – 3 = 11, так как после события (5) для завершения всего комплекса нужно выполнить работу (5,6) длительностью 3 дня. Из события (4) выходит две работы, поэтому Т п4= min{ Т п6 – t 4,6; Т п5 – t 4,5} = min{14-7; 11-5} = 6; Т п3 = 6 – 2 = 4; Т п2 = min{ Т п5 – t 2,5; Т п3 – t 2,3} = min{11– 3; 4 – 0} = 4; Т п1 = 0. Найдём резервы времени событий: R 2 = Т п2 – Т р2 = 4 – 2 = 2, резервы остальных событий в данном случае равны нулю, так как эти события критические. Расчёт сетевого графика выполняют табличным или графическим способами. Табличный способ используется для определения параметров работ, графический – параметров событий. Параметры работ сетевого графика сводят в таблицу, в которой дополнительно отражают резервы времени каждой работы (табл. 3.4). Таблица 3.4
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1092; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.87 (0.007 с.) |

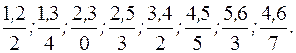 Над чертой дроби перечислены события, из которых состоит работа, под чертой – время необходимое для выполнения данной работы. При этом алгоритм построения сетевой модели не меняется.
Над чертой дроби перечислены события, из которых состоит работа, под чертой – время необходимое для выполнения данной работы. При этом алгоритм построения сетевой модели не меняется.