
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретная СВ: определение, закон распределения, функция распределения. Числовые хар-ки дсв.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Дискретной случайной величиной называется такая случайная величина, множество значений которой конечно или счетно, то есть элементы множества можно пронумеровать. Закон распределения вероятности ДСВ. Пусть ДСВ считается заданной, если известны все возможные значения СВ и соответствующие им вероятности. Определение. Законом распределения ДСВ называют соответствие между возможными значениями и их вероятностями. Закон распределения можно задать таблично, аналитически(формула) и графически. Мы будем использовать табличный. Табличный вид:
Учитывая, что в 1-ом испытании СВ примет только 1 из возможных значений, то события Х= ;…;Х= Функция распределения Определение. Функцией распределения СВ Х называется функция F(x), выражающая вероятность того, что СВ Х примет значение меньше, чем х; ∀ х е R F(x)=P(X<x) По закону распределения можно задать функцию и наоборот. Св-ва Ф-ия распределения F(x) – неубывающая,т.е. F( Пусть F( F( 0≤F(x)≤1 F(-бесконечности)=0 F(+бесконечности) = 1 Следствие. Для ДСВ функция распределения – это разрывная ступенчатая функция, непрерывная слева. Вероятность попадания СВ Х в интервал от α до β вычисляется по формуле: P(α≤x<β) = F(β)-F(α) Док-во этой формулы вытекает из 1-ого св-ва, если х1 заменить на альфа,а х2 на β. Числовые характеристики ДСВ. 1) Математическое ожидание Определение. Мат.ожиданием ДСВ, имеющей закон распределения:
Называют сумму произведений всех ее возможных значений на их вероятности. (среднее значение ДСВ) Пусть СВ Х может принимать только значения х1;х2;…;хn, вероятности которых соответственно равны p1;р2;…;рn. Тогда мат ожидание M(X) СВ Х определяется равенством: M(X)= x1p1+x2p2+…+xnpn Если ДСВ Х принимает счетное множество возможных значений, то M(X)= Св-ва M(X) 1. M(Const)=const Док-во.Будем рассматривать постоянную С как ДСВ, которая имеет одно возможное значение С и принимает его с вероятностью р=1, следовательно М(С)=С*1=С 2. M(CX)=C(M(X)) 3. M(X+Y)=M(X)+M(Y) 4. M(X1+X2+…+Xn)= M(X1)+M(X2)+…+M(Xn) Если X и Y независимы, то M(XY)= M(X)*M(Y) Если X1,X2,…,Xn – независимые, то M(X1*X2*…*Xn)= M(X1)* M(X2)*…*M(Xn). Мат ожидание называется 1-й из хар-ик положения СВ, но не единств! 2) Мода и медиана Модой ( Медианой (Me(X)) – называется такое значение Х, для которого выполняется Р(Х Р(Х Если таких значений будет 2,то медиану ищем как среднее арифметическое: Ме(Х)= 3) Дисперсия Дисперсия – рассеяние значения СВ вокруг мат. ожидания. Определение. Отклонением СВ Х от ее мат. ожидания или просто откл. СВ называется величина Х-М(Х) Теорема. М(Х-М(Х)=0 Мат ожидание отклонения = 0 М(х-М(Х))=М(Х)-М(М(Х))=М(Х)-М(Х)=0 Однако эта теорема не дает возможность определить степень рассеивания СВ Х. Такой характеристикой является квадрат отклонения СВ Х, а именно (Х-М(Х))^2 Определение. Дисперсией называется мат ожидание квадрата отклонения СВ от ее мат ожидания Д(Х)=М((Х-М(Х))^2 На практике для вычисления дисперсии используют формулу: Д(Х) = М( Для ДСВ эта формула: Д(Х) = Док-во. Мат ожидание есть постоянная величина, следовательно 2М(Х) и Д(Х)= М(Х-М(Х))^2 = М(Х^2 – 2XM(X)+M^2(X))=M(X^2)-2M^2(X) +M^2(X)=M(X^2)-M^2(X) Итак, Д(Х) = М(Х^2)-(M(X))^2 Св-ва дисперсии 1) Д(Х)≥0 Док-во. По определению дисперсии Д(С)=М((С-С)^2)=M(0)=0 Итак, Д(С) = 0 Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеивания, конечно, не имеет. 2) Д(const)=0 3) Д(СХ)=С^2(Д(Х) 4) Если X и Y – независимые СВ, то Д(Х+У)=Д(Х)+Д(У) Следствие: 1) х1;х2;…;хn – независимые СВ, то Д(х1+х2+…+хn) = Д(х1)+Д(х2)+…+Д(хn) 2) D(X+c) = D(X) 5) Если Х и У независимые, то Д(Х-У) = Д(Х)+Д(У) Ср.Квадр.отклонение. Определение. Ср.квадр.откл. называют квадратный корень из дисперсии. σ(Х) = Св-ва. σ(const)=0 σ(CX)=|C|* σ(X) σ(C+X) = σ
Действия со случайными величинами 1. Умножение на число. Пусть Х – ДСВ, заданная законом распределения
У=С*Х – эта СВ определена законом распределения
Каждое возможное значение умнож на const,а р остается прежней. Опред.2 СВ Х и У называются независимыми, если независимы все связанные с ними случайные события. Х<x;Y<y;X= То есть СВ Х и У независимы, если закон распределения каждой из них не зависит от того, какое значение примет другая СВ. Замечание. Св-во независимости является взаимным. То есть, если СВ Х не завис от У, то и У не завис от Х. 2. Сложение СВ Пусть Х и У – ДСВ, тогда Z=X+Y также является ДСВ, возм. знач которой = суммам каждого возм. значения СВ Х с каждым возм. значением СВ У. Вероятности возм знач Z для независимых СВ Х и У = произв. Вероятностей слагаемых, а для завис. = произв. Вероятности 1-ого слаг. На условную вероятность 2-ого. Заметим, что некоторые суммы Х и У могут оказаться равными между собой, тогда вероятность возможного значения суммы = сумме вероятностей. 3. Произведение. Пусть Х и У – независимые ДСВ Тогда Z=X*Y также ДСВ, возм значение которой = произведению каждого возможного значения Х на каждое возможное значение У. Вероятности возм. значений СВ Z = произв. Вероятностей возм знач сомножителей. Заметим, что нек. произв. Х*У могут оказаться равными между собой, тогда вероятность возможного значения произв = сумме соотв вероятностей. 4. Пусть Х и У – ДСВ, тогда Z=αX+βY также ДСВ.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 672; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.152 (0.006 с.) |

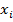 , где 1≤i≤n – это возможные значения X, тогда, если СВ Х принимает некоторое значение Х=
, где 1≤i≤n – это возможные значения X, тогда, если СВ Х принимает некоторое значение Х= 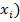
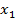

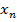




 ;Х=
;Х= 
 образуют полную группу, а значит сумма их вероятностей =1.
образуют полную группу, а значит сумма их вероятностей =1. при
при 
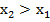
 = P(X<
= P(X<  =P(X<
=P(X<  – P(X<
– P(X<  ≥0
≥0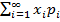
 ДСВ Х называется ее наиболее вероятное значение, то есть то значение, для которого вероятность
ДСВ Х называется ее наиболее вероятное значение, то есть то значение, для которого вероятность  достигает max. Если максимум в нескольких точках, то распределение полимодальное!
достигает max. Если максимум в нескольких точках, то распределение полимодальное!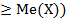 ≥1/2
≥1/2 ≥1/2
≥1/2 /2
/2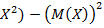

 есть также постоянные величины. Приняв это во внимание и пользуясь свойствами мат ожидания(постоянный множитель можно вынести за знак мат ожидания, мат ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии:
есть также постоянные величины. Приняв это во внимание и пользуясь свойствами мат ожидания(постоянный множитель можно вынести за знак мат ожидания, мат ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии:

 Y=
Y= 



