Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность распеределения нсв и ее свойства.Содержание книги Поиск на нашем сайте
Пл-тью р-я нсв Х в т. x наз-ся произв-я ее ф-ии р-ия в этой т-ке. f(x)=F’(x). F(x) явл первообразной д/пл-ти f(x). График пл-ти – кривая р-ия. Пл. р-ия в т-ке – это углов. коэф. касат-ой, провед-ой к ф-ии р-ия в эт. т-ке. Св-ва плотности: 1) f(x) ≥0 Док-во: по св-ву ф-ии р-ия F(x)-неуб.ф-ия., F’(x) ≥0, а тк f(x)= F’(x)то, f(x) ≥0. 2) Основн.св-во пл-ти. (условие нормировки).
Геом-ки это означ.,что вся площ. криволин. трап., огранич-ой осью ох и кривой р-ия = 1. Док-во. Несобственный интеграл Геометрически это означает, что вся площадь криволинейной трапеции, ограниченная осью Ох и кривой распределения, равна единице. В частности, если все возможные значения СВ принадлежат интервалу (а;б), то 3)P(α<x<β)= Док-во: P(α<x<β)=F(β) – F(α)= Геом. это означ, что P того, что НСВ прим. знач., принадл. пром-ку (α;β) = площ-ди кривол.трап., огран-ой осью ох, кривой р-ия и прямыми х= α, х=β. 4) F(x)= Числовые характеристики НСВ 1)Матем.ожидание нсв Х опред-ся равен-вом: M(X)= Если все возм.знач-я Xϵ [a;b], то M(X)= 3) Дисперсия нсв опр-ся рав-вом: D(X) = Если все возм.знач-я Xϵ [a;b], то D(X)= 4)Среднее квадратич. отклонение. Ϭ(X)= 5) Модой нсв X наз-ся то ее знач. аргемента, в кот. плот-ть достиг. max
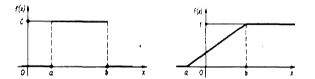
6) Медианой нсв X наз-ся то ее знач. арг-та, для кот. выполн-ся: Me(X)= Равномерное распределение НСВ (непрерывная случайная величина) Х распределена равномерно на [a; b], если ее Функция распределения выражается формулой: F(x)= Графики функций f(x) и F(x) имеют вид:
M(X)=Me(X)= Используя формулу для вычисления математического ожидания НСВ, имеем:
Таким образом, математическое ожидание случайной величины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка. D(X)= Сигма σ(X)= Mo(X) это любая точка из [a;b]: бесконечное множество. Основное свойство закона равном распределения НСВ на отрезке: вероятность попадания СВ в интервал от α до β из области определения функции пропорциональна длине этого интервала:
Равномерное распределение имеют СВ, характеризующие ошибки измерений при помощи инструмента с крупными делениями при округлении. Нормальное распределение СВ Х распределена по нормальному закону, если
Где а и s—некоторые постоянные, называемые параметрами нормального распределения, которых достаточно для задания норм распр. a=M(X) s=s(X) График плотности – нормальная кривая Гаусса. Исследуем ее, чтобы построить: 1°. Областью определения функции f(x) является вся числовая ось. 2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0. 3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции. 4°. Функция f{x) имеет в точке х = a максимум, равный
5°. График функции f(x) симметричен относительно прямой х = а. 6°. Нормальная кривая в точках х = а +s имеет перегиб,
На основании доказанных свойств построим график плотности нормального распределения f(x).
Выясним влияние а и s: 1. Изменение а не изменяет форму кривой, но приводит к ее сдвигу вдоль Ох вправо при возрастании а и влево при убывании 2. При увеличении s нормальная кривая становится более пологой, при уменьшении – более острой 3. При любых а и s площадь под графиком равна 1. Для вычисления вероятности попадания в интервал вводится функция Лапласа
Свойства:
Φ(0)=0 При f(x)˃5 Φ(x)=0,5 Для вычисления вероятности попадания
Часто необходимо вычислить вероятность отклонения нормального распределения Х по абсолютной величине, не большей заданного положительного числа.
(функция Лапласа—нечетная), окончательноимеем
Чем меньше
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.42.61 (0.005 с.) |

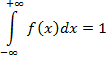
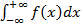 выражает вероятность события, состоящего в том, что Св примет значение, принадлежащее интервалу (-
выражает вероятность события, состоящего в том, что Св примет значение, принадлежащее интервалу (- 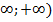 . Очевидно, такое событие достоверно, следовательно, вероятность его = 1.
. Очевидно, такое событие достоверно, следовательно, вероятность его = 1.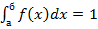

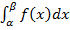 , По ф-ле Ньютона-Лейб.
, По ф-ле Ньютона-Лейб.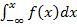 Док-во: по опр-нию, ф-ия р-ия F(x)=P(X<x)=P(-∞<X<x)=
Док-во: по опр-нию, ф-ия р-ия F(x)=P(X<x)=P(-∞<X<x)= 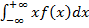

 или =
или =  = M(
= M( ) -
) - 

 свойства такие же, как для ДСВ
свойства такие же, как для ДСВ (X)= x max f(x)
(X)= x max f(x) , F(
, F( )=1/2
)=1/2







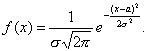
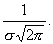
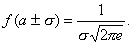








 , т.е. чем меньше рассеяние СВ Х вокруг ее М(Х), тем больше вероятность для СВ попасть в интервал от –
, т.е. чем меньше рассеяние СВ Х вокруг ее М(Х), тем больше вероятность для СВ попасть в интервал от –  . Если радиус интервала с центром в точке х=а взять равным 3
. Если радиус интервала с центром в точке х=а взять равным 3  , то почти все возможные значения СВ Х окажутся в этом интервале. Правило 3 сигма: если СВ распределена нормально, то абсолютная величина ее отклонения от М(Х) не превышает утроенного среднего квадратического отклонения
, то почти все возможные значения СВ Х окажутся в этом интервале. Правило 3 сигма: если СВ распределена нормально, то абсолютная величина ее отклонения от М(Х) не превышает утроенного среднего квадратического отклонения