
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы счета времени: местное, всемирное, поясное, летнее и декретное время. Долгота. Линия перемены даты. Календари. Юлианские дни.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Время определяется в некоей системе отсчёта, которая может быть как неравномерная (процесс вращения Земли вокруг Солнца или человеческий пульс), так и равномерная. Равномерная эталонная система отсчёта выбирается «по определению», ранее, например, её связывали с движением тел Солнечной системы (эфемеридное время), а в настоящее время таковой локально считается атомное время, а эталон секунды — 9 192 631 770 периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 при отсутствии возмущения внешними полями. Следует отметить, что это определение — не произвольное, а связанное с наиболее точными периодическими процессами, доступными человечеству на данном этапе развития экспериментальной физики: Ме́стное вре́мя — одинаковое время в один момент суток в точках, расположенных на одном меридиане. Конкретно, под местным временем могут пониматься: Поясное время в данном конкретном месте — это наиболее частое подразумеваемое значение; Среднее солнечное время на данном меридиане; Местное солнечное время на данном меридиане с учётом изменяемой продолжительности астрономических суток, также называемое в астрономии «Истинное солнечное время», и отсчитываемое от моментов астрономических полуночи и полудня. Всеми́рное координи́рованное вре́мя (UTC) — стандарт, по которому общество регулирует часы и время. Отличается на целое количество секунд от атомного времени и на дробное количество секунд от всемирного времени UT1. UTC было введено вместо устаревшего среднего времени по Гринвичу (GMT). Новая шкала времени UTC была введена, поскольку шкала GMT является неравномерной шкалой и связана с суточным вращением Земли. Шкала UTC основана на равномерной шкале атомного времени (TAI) и является более удобной для гражданского использования. Так как между UTC и UT1 разница не превышает 0,9 с, если не требуется высокая точность, может использоваться более общее понятие Всемирное время (UT). В повседневной жизни, когда дробная часть секунд не важна, среднее время по Гринвичу (GMT) может рассматриваться как эквивалент UTC или UT1. В противном случае, когда разница между UTC и UT1 существенна, использования термина среднее время по Гринвичу (GMT) избегают. Часовые пояса вокруг земного шара выражаются как положительное и отрицательное смещение от UTC. Следует помнить, что время по UTC не переводится ни зимой, ни летом. Поэтому для тех мест, где есть переход на летнее время, смещение относительно UTC меняется. Понятие часово́й по́яс имеет два основных значения: Географический часово́й по́яс — полоса на земной поверхности шириной ровно 15° (± 7,5° относительно среднего меридиана). Средним меридианом нулевого часового пояса считается гринвичский меридиан. Административный часово́й по́яс (или, в соответствии с новым законом «Об исчислении времени»[1], — часовая зона) — участок земной поверхности, на котором в соответствии с некоторым законом установлено определённое поясное время. Как правило, в понятие административного часового пояса включается ещё и совпадение даты — в этом случае пояса UTC−10 и UTC+14 будут считаться различными, хотя в них действует одинаковое время суток. В большинстве случаев, если не указывается, какое именно значение часового пояса подразумевается, речь идёт об административном часовом поясе. Формирование административных часовых поясов (часовых зон — time zones) связано со стремлением, с одной стороны, учитывать вращение Земли вокруг своей оси, а с другой стороны, определить территории (временные зоны) с примерно одинаковым местным временем таким образом, чтобы различия во времени между ними были кратны одному часу. В результате было достигнуто решение, что должно быть 24 административных часовых пояса и каждый из них должен более-менее совпадать с географическим часовым поясом. Точкой отсчёта был принят гринвичский меридиан, нулевой меридиан, средний меридиан нулевого часового пояса. Сейчас время устанавливается при помощи всемирного координированного времени (UTC), которое было введено взамен времени по Гринвичу (GMT). Шкала UTC базируется на равномерной шкале атомного времени (TAI) и является более удобной для гражданского использования. Часовые пояса вокруг земного шара выражаются как положительное и отрицательное смещение от UTC. (Отрицательные смещения у часовых поясов к западу от нулевого меридиана, положительные — к востоку.) Следует помнить, что время по UTC не переводится ни зимой, ни летом. Поэтому для тех мест, где есть перевод на летнее время, смещение относительно UTC меняется. В основу современной системы часовых поясов положено всемирное координированное время, от которого зависит время всех часовых поясов. Для того чтобы не вводить местное время для каждого градуса (или каждой минуты) долготы, поверхность Земли условно поделена на 24 часовых пояса. При переходе из одного часового пояса в другой, значения минут и секунд (времени) сохраняются, изменяется лишь значение часов. Существуют некоторые страны, в которых местное время отличается от всемирного не только на целое количество часов, но ещё дополнительно на 30 или 45 мин. Правда, такие временные зоны не являются стандартными часовыми поясами. Теоретически 24 часовых пояса земного шара должны ограничиваться меридианами, проходящими на 7°30' восточнее и западнее среднего меридиана каждого пояса, причём вокруг гринвичского меридиана действует всемирное время. Однако в реальности для сохранения единого времени внутри одной и той же административной или природной единицы границы поясов смещены относительно меридианов; местами некоторые часовые пояса даже «пропадают», теряясь между соседними[2]. На Северном и Южном полюсах меридианы сходятся в одной точке, и поэтому там понятие часовых поясов, а заодно и местного времени, теряет смысл. Считается, на полюсах должно использоваться всемирное время, однако на станции Амундсен-Скотт (Южный полюс) действует время Новой Зеландии. Ле́тнее вре́мя — время, сдвинутое на 1 час вперёд относительно времени, принятого в данном часовом поясе. Вводится во многих странах в летний период с целью экономии электроэнергии на освещение. В зимний период время «сдвигают» обратно, возвращаясь к «зимнему времени» (этот термин не является официальным). В большинстве стран «зимнее время» совпадает со стандартным астрономическим временем часового пояса, хотя есть и исключения из этого правила. Критики летнего времени говорят о негативном влиянии перевода часов на здоровье людей и указывают на то, что экономическая польза летнего времени не доказана. В России ежегодный переход на летнее время существовал до лета 2011 года, когда переход на зимнее время был отменён и летнее время стало постоянным. По данным социологических опросов, большинство населения России выступало против перевода стрелок часов Декре́тное вре́мя является одним из способов использования в стране или на какой-либо территории такого времени, которое опережает «своё время» (время своего географического часового пояса) на один час. Формальной отличительной особенностью применения декретного времени от иных способов использования опережающего времени является добавление к поясному времени т. н. «декретного часа» при формальном сохранении нумерации часовых поясов. Так, например, по сути ситуация в Париже и Санкт-Петербурге (до 27 марта 2011 г.) одна и та же: официальное время в Париже и декретное время в Санкт-Петербурге (бывшее «зимнее» до 27 марта 2011 г.) опережают поясное на 1 час, однако для Парижа это оформлено как перемещение территории из нулевого в первый часовой пояс (UTC --> UTC+1), а для Санкт-Петербурга — сохранение территории во втором часовом поясе, но с прибавлением декретного часа: (UTC+2)+1 = UTC+3. Долгота́ — координата в ряде систем сферических координат, определяющая положение точек на поверхности Земли, Солнца, планет и на небесной сфере относительно нулевого меридиана, от которого ведётся отсчёт долгот. Долгота λ — это угол между плоскостью меридиана, проходящего через данную точку, и плоскостью нулевого меридиана. Выбор нулевого меридиана произволен и определяется соглашением. Нулевой меридиан, проведённый через Гринвич, называется Гринвичским меридианом. Кроме Гринвича, в качестве нулевого ранее принимались меридианы обсерваторий Кадиса, Парижа, Пулковский меридиан и т. д. Долготы от 0 до 180° к востоку от нулевого меридиана называют восточными, к западу — западными. Восточные долготы принято считать положительными, западные долготы — отрицательными. Ли́ния переме́ны да́ты — условная линия на поверхности земного шара, проходящая от полюса до полюса, по разные стороны которой местное время отличается на сутки (или почти на сутки). То есть, по разные стороны часы показывают примерно одно время суток (возможна разница на один-три часа из-за смены часовых поясов), однако на западной стороне линии дата сдвинута на один день вперёд относительно восточной. Примерно соответствуя меридиану 180°, проходящему в основном по океану, на практике линия перемены дат определена местами довольно плохо. Не существует никакого международного соглашения относительно линии смены дат, ведь местное время определяется правительствами на своей территории и прилегающих территориальных водах, а не в международных водах Океана. Линия перемены даты нигде, кроме Антарктиды, не проходит по суше, хотя есть случаи, когда она проведена между близко расположенными островами, например, между островами Диомида, которые находятся на расстоянии всего 4 км друг от друга. Северная часть линии перемены даты начинается в Ледовитом океане, огибает с востока восточные территории Российской Федерации, входит в Тихий океан через Берингов пролив, южнее переходит на западную сторону меридиана 180°, оставляя на востоке от себя Алеутские острова, после чего снова выходит на меридиан 180°. Далее линия следует по Тихому океану до самой Антарктиды, испытывая ещё одно крупное отклонение к востоку в Океании (Кирибати и др.). Касательно этого участка следует отметить, что следующее по Тихому океану судно вполне может игнорировать время близлежащих островов Океании и осуществлять перевод дат на меридиане 180°. При пересечении линии перемены даты в направлении из Западного Полушария в Восточное, в счете календарных дат прибавляют один день (переходят к завтрашней дате); при движении же из Восточного в Западное — возвращаются на один день назад (переходят ко вчерашней дате). Перемена дат должна осуществляться только при использовании, в той или иной форме, местного времени. Непонимание этого обстоятельства приводит к «парадоксам» касательно обхода земного полюса по кругу или облёта Земли по орбите. Календа́рь (лат. calendarium — долговая книжка: в Древнем Риме должники платили проценты в день календ, первых чисел месяца) — система счисления больших промежутков времени, основанная на периодичности движения небесных тел: Солнца — в солнечных календарях, Луны — в лунных календарях и одновременно Солнца и Луны в лунно-солнечных календарях. Счёт года с 1 января был введён в Риме Юлием Цезарем в 45 году до н. э. (юлианский календарь). В 325 году юлианский календарь был принят Византией. На Руси с 1492 года началом года стало считаться не 1 марта, а 1 сентября. Юлианский календарь установил среднюю продолжительность года в 365,25 суток: обычные годы длились 365 дней, один раз в четыре года (високосный год) — 366 дней. Современный календарь назван григорианским (новый стиль). Он введён при папе римском Григории XIII 15 октября 1582 года взамен юлианского календаря (старого стиля). Реформа, которую провёл Григорий XIII и признали в большинстве католических стран, состояла из двух частей: 1) Была устранена ошибка в 10 дней, накопившаяся со времен I Вселенского собора (325 год), на котором были установлены правила вычисления христианской Пасхи. Бытует неверное мнение, что папа Григорий XIII исправил ошибку, накопившуюся с момента введения юлианского календаря. Но тогда это было бы 12 дней. Однако, целью реформы было иное: «вернуть» дату реального весеннего равноденствия (пасхальную границу) на 21 марта, как это было во времена Никейского собора, установившего пасхалию. 2) На будущее же была введена поправка, обеспечивающая более точное соответствие с солнечным исчислением, которая заключается в том, что из каждых 400 лет должны были быть исключены три високосных года. Таким образом, ошибка в один день накапливается лишь через 3333 года. Исключение трёх високосных лет за четыре века достигалось следующим правилом. Если номер года заканчивается не на два нуля, то он считается високосным тогда, когда номер года кратен четырём (например, 1996, 2004, 2008 годы). Если год заканчивается на два нуля, то он високосный только тогда, когда число сотен в нём также кратно четырём (например, 1600, 2000, 2400 годы). Во всех остальных случаях год считается невисокосным (например, 1900 и 2100 годы). Правило определения «високосности» года, заканчивающегося на два нуля, является одной из отличительных особенностей григорианского календаря по сравнению с юлианским. Разница между старым и новым стилями составляла в XVI—XVII веках 10 суток, XVIII веке — 11 суток, в XIX веке — 12 суток, в XX-XXI веках составляет 13 суток.
7. Факторы, искажающие положения светил на небе. Рефракция. Суточная и годичная аберрации. Суточный и годичный параллаксы. Собственные движения звёзд. Единицы измерения расстояний в астрономии. Методы определения расстояний до светил и размеров небесных тел Солнечной системы.
В результате преломления лучей света в атмосфере наблюдатель видит светило в точке M 1, а не в точке M 2 в случае отсутствия Атмосферы. Явление преломления световых лучей при прохождении ими земной атмосферы называется астрономической рефракцией ∠ M 1 OM 2 = ρ (угол рефракции) ∠ ZOM 1 = z ' (видимое зенитное расстояние) ∠ ZOM 2 = z (истинное зенитное расстояние) • Рефракция «приподнимает» светила над горизонтом • Рефракция не изменяет азимутов светил и, очевидно, равна нулю для светил в зените • В кульминации рефракция искажает склонение, но не искажает прямое восхождение • Вследствие рефракции наблюдается изменение формы дисков Солнца и Луны при их восходе и закате. Рефракция нижних краёв дисков у горизонта почти на 6' больше рефракции верхних краёв, а, т.к. горизонтальные диаметры рефракцией не изменяются, то видимые диски Солнца и Луны принимают овальную форму • На горизонте ρ = 35'
Аберрацией светила называется явление, состоящее в том, что движущийся наблюдатель видит светило не в том направлении, в котором он видел бы его в тот же момент, если бы находился в покое ∠ M'K 0 A = θ (угловое расстояние видимого направления на звезду от точки неба, в которую направлена скорость наблюдателя) ∠ M'OM = σ (аберрационное смещение) Суточная аберрация – следствие конечности скорости света в сочетании со скоростью суточного вращения наблюдателя, годичная – в сочетании со скоростью годичного движения, т.е. движения Земли по орбите (v = 29,78 км/с) σ = 20,50'' sin θ
Координаты одного и того же небесного тела, определённые с Земли, разные в различных точках её поверхности. Такие координаты называются топографическими. Зависимость координат светила от точки наблюдения на Земле связана со смещением проекции светила на небесной сфере, которое называется параллаксом. Основным считается направление на светило из центра Земли. Такое направление даёт геоцентрическое положение светила и определяет его геоцентрические координаты. Суточный параллакс – это угол, под которым со светила был бы виден радиус Земли. Для светила в зените параллакс равен нулю. Если светило наблюдается на горизонте, то суточный параллакс принимает максимальное значение и называется горизонтальным параллаксом p. p' = p sin z' Горизонтальный параллакс для объектов Солнечной системы: у Луны p = 57', у Солнца p = 8,79''. Горизонтальные параллаксы, вычисленные для экваториального радиуса Земли R 0 = 6 378 км, называются горизонтальными экваториальными параллаксами
Угол, под которым со звезды был бы виден средний радиус земной орбиты a при условии, что направление на звезду перпендикулярно радиусу, называется годичным параллаксом π звезды. Расстояние до звезды:
Т.к. параллаксы всех звёзд меньше 1 '', то:
Окончательно:
Расстояние Δ получается в тех же единицах, в которых выражен средний радиус земной орбиты a Собственным движением называются изменения координат звёзд на небесной сфере, вызванные относительным движением звёзд и Солнечной системы. В них не включают периодические изменения, вызванные движением Земли вокруг Солнца (параллакс). Более строгое определение: «Собственным движением звезды в астрономии называют величины, характеризующие её угловое перемещение на небесной сфере в заданной системе координат за единицу времени» Если какая-либо звезда наблюдалась дважды в эпоху t1 и эпоху t2 и её видимые координаты — прямое восхождение (α) и склонение (δ) — приведены в систему фундаментального каталога FK5 (эпоха T0), то её собственное движение определяется как
размерность — секунда времени в год,
размерность — угловая секунда в год. Определённые таким способом собственные движения звёзд иногда называют меридианными, так как они определяются в результате сравнения двух положений, полученных посредством наблюдений на меридианных кругах. Массовые определения меридианных собственных движений звёзд стали возможными уже в XIX веке в результате создания нескольких десятков меридианных каталогов, приведённых к некоторой одной фундаментальной системе. Наибольшее число (33 342) положений и собственных движений звёзд (в том числе слабых — до 9-й звёздной величины) в одной системе приведено в известном общем каталоге «General Catalogue» Льюиса Босса (1910 год). Ошибки собственных движений в этом каталоге составляют ± (0.005—0.15)″/год. Положения и движения звёзд несвободны от систематических ошибок. Новые фундаментальные каталоги звёзд FK4 и FK5 сохраняют ошибки собственных движений на уровне ± (0.002—0.005)″/год, однако эти каталоги охватывают лишь небольшое число избранных, в основном ярких звёзд. К 1995 году было известно не менее 50 000 меридианных собственных движений звёзд от самых ярких до 9-й звёздной величины. Ошибки этих собственных движений могут быть от ± 0.002″ до ± 0.010″ в зависимости от продолжительности истории наблюдений. По величине большинство известных собственных движений меньше 0.050″/год, однако встречаются и большие собственные движения. Так, самое высокое значение собственного движения имеет «летящая» Звезда Барнарда — 10.358″. Вторую и третью строчку в рейтинге самых быстро перемещающихся звёзд на небесной сфере занимают Звезда Каптейна (8.670″/год) и Лакайль 9352 (6.896″/год). Единицы измерения расстояний в астрономии • Астрономическая единица (а.е.) – среднее расстояние Земли от Солнца (средний радиус земной орбиты). 1 а.е. = 149 600 000 км • Парсек (пк) – расстояние, соответствующее годичному параллаксу в 1 ''
• Световой год – расстояние, которое свет в вакууме проходит за один год, распространяясь со скоростью 299 792,458 км/с 1 св. год = 9,460·1012 км = 63 240 а.е. = 0,3067 пк Методы определения расстояний до светил • Определение расстояний до тел Солнечной системы основано на измерении их суточных горизонтальных параллаксов • Суточный горизонтальный параллакс светила можно определить, измерив прямое восхождение светила α из одного и того же места на Земле, но в различные моменты времени • Расстояния до тел Солнечной системы можно определять также радиолокационными методами • Расстояния до звёзд определяются по их годичному параллактическому смещению. В этом случае измеряются геоцентрические координаты звезды из наблюдений, произведённых в двух различных точках орбиты Земли приблизительно через полгода одно после другого • Наилучшие современные определения годичных параллаксов выполняются с космических аппаратов, при этом достигается точность в 0,001" • В настоящее время годичные параллаксы (т.е. расстояния) измерены для более чем 100 тысяч звёзд (из них только 16 тысяч – на основании наземных наблюдений)
На основе измеренных горизонтальных параллаксов можно определить линейные размеры небесных тел Солнечной системы ρ – угловой радиус светила (половина угла, под которым с Земли виден диск светила), R 0 – линейный радиус Земли, r – линейный радиус светила, p 0 – горизонтальный экваториальный параллакс светила r = Δ sin ρ, R 0 = Δ sin p 0
Практические задачи астрометрии. Определение всемирного времени. Поправка часов. Ход часов. Определение географической долготы. Определе ние географической широты и поправки часов. Абсолютные и относительные методы измерения экваториальных координат. Практические задачи астрометрии: • Определение точного времени • Определение географических координат пунктов на поверхности Земли • Измерение точных координат светил Определение всемирного времени. Поправка часов. Ход часов. Определение географической долготы Разность между временем T в какой-то момент по стандартной шкале и показаниями рабочих часов T' в этот момент называется поправкой часов u: u = T – T' или T = T' + u Изменение поправки часов за определённый промежуток времени называется ходом часов ω:
С помощью астрономических наблюдений определяется местное звёздное время (s), которое далее пересчитывается в среднее солнечное, т.е. в точное время (T): s = α + t = T = T' + u или u = α + t – T' Если отметить показания часов T' в момент верхней кульминации (t = 0), то u = α – T' Зная поправку часов u, определяют всемирное время (Universal Time, UT). Из сравнения шкал всемирного и атомного времени определяют неравномерность вращения Земли Определение географической долготы λ сводится к вычислению разности местного времени на данном географическом меридиане и времени гринвичского меридиана: λ = Tm – T 0 = u – u 0 Определение географической широты и поправки часов 1) Определение φ и u по измеренным зенитным расстояниям cos z = sin φ sin δ + cos φ cos δ cos t и t = T' + u – α (1) Если для двух (или более) светил, для которых по Астрономическому ежегоднику известны α и δ, измерены z (или h) по звёздным часам в момент времени T', то по (1) можно найти φ и u. 2) Определение φ и u в момент кульминации (t = 0 или 12h) Для верхней кульминации к югу от зенита: φ = δ + z (2) Для верхней кульминации к северу от зенита: φ = δ – z (3) Для нижней кульминации: φ = 1800 – δ – z (4) Т.о., по известному δ и измеренному z из (2) – (4) определяют широту Поправка часов для верхней кульминации: u = α – T' (5) Поправка часов для нижней кульминации: u = α – T' + 12h (6) Абсолютные и относительные методы измерения экваториальных координат. Абсолютный метод определения склонений Измеряются зенитные расстояния (или высоты) незаходящей звезды в верхней и нижней кульминации: z в.к. = δ –φ и z н.к. = 1800 – φ – δ Откуда: δ = 900 – ½ (z н.к. – z в.к.) и φ= 900 – ½ (z н.к. + z в.к.) Т.е. определена широта места наблюдения и склонение одной звезды. Аналогичным образом находятся φ и δ для нескольких незаходящих звёзд, и значение φ усредняется. Далее по формулам (2) – (4) находятся склонения других звёзд (в т.ч. и заходящих).
Вблизи дней солнцестояний (т.е. когда δŸ принимает экстремальные значения) проводят измерения δŸ, абсолютная величина которого = ε. Далее вычисляется αŸ и s = αŸ = T' Ÿ + u, т.е. поправка часов. Выбираются 30 – 40 ярких звёзд, равномерно расположенных вдоль эклиптики и небесного экватора, и которые можно наблюдать до или после наблюдений Солнца. Такие звёзды называются часовыми. При наблюдении часовых звёзд определяют их моменты прохождения через меридиан (кульминации): T' 1, T' 2, …, T'n. При наблюдении Солнца определяется момент его прохождения через меридиан T' Ÿ и зенитное расстояние в этот момент z Ÿ. Далее вычисляется δŸ и αŸ, а также поправки и ход часов на каждый день наблюдения. Для каждого дня наблюдения составляют уравнения для Солнца и часовых звёзд: αŸ = T' Ÿ + u, α1 = T' 1 + u 1, …, α n = T'n + un. В уравнении для Солнца известны все величины, а в уравнениях для часовых звёзд – величины T'i и поправки часов: ui = u + ω(T'i – T' Ÿ). Т.о. можно определить прямые восхождения звёзд абсолютным методом: α i = T'i + u + ω(T'i – T' Ÿ). В этом методе наблюдения Солнца необходимы для фиксации положения точки ¢ среди звёзд. С этой целью вместо Солнца можно наблюдать любую планету (в т.ч. и малую) Солнечной системы. Относительные методы В относительных методах определение координат сводится к измерению разностей Δδ и Δα определяемых и опорных звёзд: T – Ti = α – α i = Δα i. z – zi = δ – δ i = Δδ i
Теоретическое обеспечение и инструменты практической астрономии. Астрономические каталоги, карты и атласы звёздного неба. Угломерные инструменты: универсальный инструмент, секстант, меридианный круг, зениттелескоп, призменная астролябия. Астрономические каталоги • В астрономических каталогах содержаться средние координаты звезд, т.е. экваториальные координаты после того, как из них вычтены различные поправки (рефракция, аберрация и др.). • Каталоги положений составляются на начало определённого года. На основании каталогов положений составляются фундаментальные каталоги, в которых, кроме экваториальных координат, указывается собственное движение звезды, параллаксы и другие данные. • Первый каталог (более 850 звёзд) был составлен Гиппархом во II веке до н.э. • Общий каталог Босса (General Catalog, GC) был создан Л. Боссом в 1937 г. И содержит 33 342 звёзд до 7 m. • С помощью радиоастрономических наблюдений была создана новая система привязки системы отсчёта небесных координат к очень удалённым, т.е. устойчивым радиоисточникам (International Celestial Reference System, ICRS). • Специальные космические аппараты («Гиппаркос», HIPPARCOS, 1989–1993) позволили измерить с точностью до 0,001" координаты, собственные движения и параллаксы 118 218 объектов (каталог Гиппаркос). Каталог Гиппаркос обеспечивает систему координат ICRS, т.е. привязан к внегалактическим объектам. • В каталоге Тихо содержаться аналогичные данные для более чем 2 000 000 объектов с точностью от 0,007 до 0,025". • Кроме звёздных каталогов, имеются каталоги других небесных объектов • «Каталог туманностей и звёздных скоплений» («Catalogue des Nébuleuses et des Amas d'Étoiles») был составлен Ш. Мессье (Charles Messier) в 1781 г. и включал 103 объекта. Обозначения в этом каталоге: M 31 – Туманность Андромеды • «Новый общий каталог туманностей и звёздных скоплений» («A New General Catalogue of Nebulae and Clusters of Stars, being the Catalogue of the late Sir John F.W. Herschel, Bart., revised, corrected, and enlarged», NGC) составлен Й. Дрейером (John Louis Emil Dreyer) в 1888 г. и содержал данные о 7 840 объектах. К настоящему времени издано два дополнения (IC I и IC II), в которых содержатся данные ещё о 5 386 объектах. Обозначения: NGC 224 – Туманность Андромеды • Существуют каталоги и других небесных объектов – двойных звёзд, рентгеновских и радиоисточников и др. • Астрономические ежегодники Карты и атласы звёздного неба • «Уранография: описание всего звёздного неба» («Uranographia: totum caelum stellatum») — атлас звёздного неба Яна Гевелия (Johannes Hevelius). Издан в 1690 г. • Атлас включает 56 карт. На картах с точностью в одну угловую минуту нанесены 1564 звезды по каталогу Гевелия. Атлас Гевелия достиг точности одного порядка с бумажными картами и атласами нашего времени. Универсальный инструмент • Универсальный инструмент (УИ) – один из основных угломерных инструментов, позволяющий в любой точке земной поверхности измерять горизонтальные координаты светила. • УИ состоит из астрономической трубы, которая может поворачиваться вокруг двух взаимно перпендикулярных осей – горизонтальной и вертикальной. Углы поворота вокруг одной и второй оси отсчитываются по двум кругам (или лимбам) – вертикальному и горизонтальному. • УИ используется почти исключительно как переносный инструмент в различных экспедициях для определения географических координат места наблюдения и азимутов земных предметов. • Если в УИ вертикальный круг разделён более точно, чем горизонтальный, то такой инструмент называется вертикальным кругом. Если наоборот – то теодолитом. Секстант • Секстант (секстан) — это измерительный инструмент, используемый для измерения величины угла между двумя видимыми объектами. • Обычно секстант используется для измерения высоты астрономического объекта над горизонтом с целью Определения географических координат. Меридианный круг • Меридианный круг (МК) состоит из астрономической трубы, которая может вращаться только вокруг горизонтальной оси. Эта ось лежит на жёстко закрепленных основах. • Горизонтальная ось МК должна быть направлена точно с востока на запад. Тогда труба будет располагаться и вращаться точно в плоскости небесного меридиана. • МК позволяет измерять зенитные расстояния светил в момент кульминации, т.е. определять склонения светил. • Если отметить по часам момент кульминации, то с помощью МК можно определить и прямое восхождение Светила Зенит-телескоп • Зенит-телескоп служит для точного измерения малых разностей зенитных расстояний вблизи зенита. • Систематические наблюдения на зенит-телескопах ведутся для определения точных значений географической широты места наблюдения с целью изучения движения полюсов Земли.
Астрономо-геодезический инструмент для определения широты места и поправки часов по наблюдаемым моментам прохождения звёзд в различных азимутах через некоторый альмукантарат, Призменная астролябия может быть использована также для определения экваториальных координат звёзд и планет. Перед объективом 3 горизонтально расположенной астрономической трубы (для компактности оптическая ось трубы изломана с помощью двух зеркал 4 и 5) помещается равносторонняя стеклянная призма 1. Под призмой устанавливается ртутный горизонт 2. Свет от наблюдаемой звезды, падая на верхнюю грань призмы и преломляясь, даёт её изображение в фокальной плоскости объектива; второе изображение этой же звезды получается от её света, проходящего через нижнюю грань призмы после отражения от ртутного горизонта. Вследствие видимого суточного движения звезды оба изображения приближаются друг к другу и совпадают; в момент прохождения звезды через альмукантарат с зенитным расстоянием, близким к 30°, изображения рассматриваются в окуляр 6. Для регистрации момента микрометр инструмента имеет специальную призму Волластона 7, перемещая которую микрометрическим винтом, снабженным контактным барабаном, записывают на хронографе серию моментов, что позволяет повысить точность окончательного результата.
10. Видимые движения планет на фоне звёзд. Системы мира Клавдия Птолемея, Николая Коперника и Тихо Браге. Конфигурации планет. Синодические и сидерические периоды обращения планет. Гелиоцентрические и геоцентрические долготы. Великие противостояния Марса. Парад планет. Видимые движения планет на фоне звёзд • По видимым движениям планеты делятся на две группы – нижние, или внутренние (Меркурий и Венера) и верхние, или внешние (все остальные, кроме Земли). • Нижние планеты не отклоняются далеко от Солнца (Меркурий – на 18-280, Венера – на 45-480). Верхние планеты отходят от Солнца на 1800.
Система мира Птолемея Для объяснения видимых движений Солнца, Луны, звёзд и планет древнегреческий учёный Клавдий Птолемей (около 87–165 н.э.) предложил в труде «Альмагест» геоцентрическую систему мира: 1. Земля шарообразна и находится в центре Вселенной; 2. Земля неподвижна; 3. Все небесные тела движутся вокруг Земли; 4. Движение небесных тел происходит по окружностям с постоянной скоростью. Суточное движение всех светил объяснялось вращением Вселенной как одного целого вокруг неподвижной Земли Система мира Коперника В труде «Об обращениях небесных сфер» (1543) Николай Коперник (1473–1543) разработал гелиоцентрическую систему мира: 1. В центре мира находится Солнце; 2. Шарообразная Земля вращается вокруг своей оси и это вращение объясняет кажущееся суточное движение всех светил; 3. Земля, как и другие планеты, обращается вокруг Солнца по окружности, и это обращение объясняет видимое движение Солнца среди звёзд; 4. Все движения представляются в виде равномерных круговых движений; 5. Кажущиеся прямые и попятные движения планет принадлежат не им, а Земле. В результате анализа наблюдательных данных Коперник пришёл к выводу, что все планеты, в т.ч. и Земля, движутся вокруг Солнца примерно в одной плоскости. Луна движется вокруг Земли и, как спутник, вместе с Землёй – вокруг Солнца. Т.к. Меркурий и Венера (нижние или внутренние планеты) в видимых движениях не отходят далеко от Солнца, то их орбиты расположены ближе к Солнцу, чем орбита Земли. Чем дальше внутренняя планета отходит от Солнца, тем больше радиус её орбиты. Остальные планеты (Марс, Юпитер и Сат
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 3219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.165 (0.015 с.) |

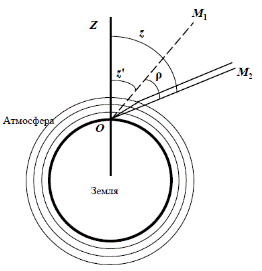 Рефракция
Рефракция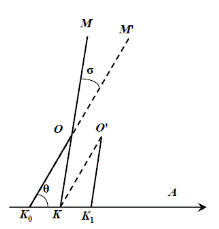 Суточная и годичная аберрации
Суточная и годичная аберрации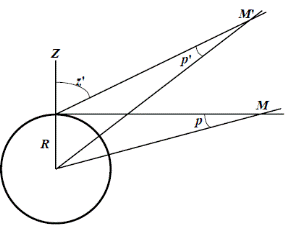 Суточный параллакс
Суточный параллакс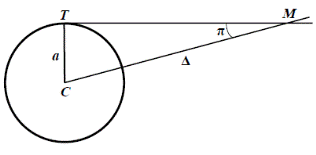 Годичный параллакс
Годичный параллакс
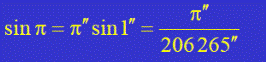

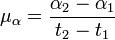
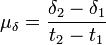
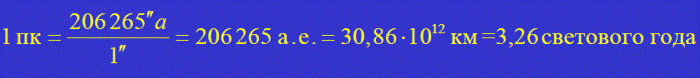
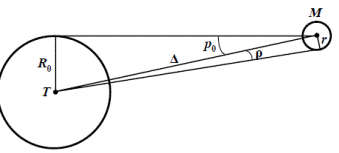 Метод определения размеров небесных тел Солнечной системы
Метод определения размеров небесных тел Солнечной системы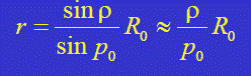

 Абсолютный метод определения прямых восхождений
Абсолютный метод определения прямых восхождений ε ε' – эклиптика, QQ' – небесный экватор, ε – наклонение эклиптики к экватору (угол между плоскостями), mC – склонение центра Солнца δŸ (дуга на поверхности сферы), ϒ m – прямое восхождение Солнца αŸ. Сферический треугольник ϒ mC – прямоугольный, поэтому:
ε ε' – эклиптика, QQ' – небесный экватор, ε – наклонение эклиптики к экватору (угол между плоскостями), mC – склонение центра Солнца δŸ (дуга на поверхности сферы), ϒ m – прямое восхождение Солнца αŸ. Сферический треугольник ϒ mC – прямоугольный, поэтому: Призменная астролябия
Призменная астролябия • Видимые движения нижних планет происходят следующим образом. В момент наилучшей вечерней видимости Венера находится в восточной элонгации (в наибольшем угловом удалении от Солнца к востоку). Затем Венера движется попятным движением (с востока на запад) и приближается к Солнцу, проходит между Солнцем и Землёй (нижнее соединение). Затем Венера продолжает двигаться попятным движением и достигает западной элонгации (момента наилучшей утренней видимости), где нижняя планета останавливается. Далее планета двигается прямым движением (с запада на восток), проходит за Солнцем (верхнее соединение) и опять достигает восточной элонгации.
• Видимые движения нижних планет происходят следующим образом. В момент наилучшей вечерней видимости Венера находится в восточной элонгации (в наибольшем угловом удалении от Солнца к востоку). Затем Венера движется попятным движением (с востока на запад) и приближается к Солнцу, проходит между Солнцем и Землёй (нижнее соединение). Затем Венера продолжает двигаться попятным движением и достигает западной элонгации (момента наилучшей утренней видимости), где нижняя планета останавливается. Далее планета двигается прямым движением (с запада на восток), проходит за Солнцем (верхнее соединение) и опять достигает восточной элонгации.


