
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и задачи астрономии. Разделы астрономии. Основные этапы развития астрономии. Общее представление о масштабах и структуре Вселенной и физическом состоянии вещества.Стр 1 из 26Следующая ⇒
Предмет и задачи астрономии. Разделы астрономии. Основные этапы развития астрономии. Общее представление о масштабах и структуре Вселенной и физическом состоянии вещества. Предмет и задачи астрономии • Астрономия – наука о Вселенной, изучающая расположение, движение, строение, происхождение и развитие небесных тел и образованных ими систем • Астрономия исследует Солнце, звёзды, планеты и их спутники, кометы, метеоры, туманности, звёздные системы, вещество, заполняющее пространство между звёздами и планетами Основные задачи: 1. Изучение видимых, а затем и действительных положений и движений небесных тел в пространстве, определение их размеров и формы 2. Изучение строения небесных тел, исследование химического состава и физических свойств вещества в них 3. Решение проблемы происхождения и развития отдельных небесных тел и образуемых ими систем Разделы астрономии: Принято выделять три основных раздела: 1. астрометрию (Астрометрия изучает положение и движение небесных тел и Земли. У астрометрии две важные цели: 1. Установление системы небесных координат; 2. Получение параметров, наиболее полно характеризующих закономерности движения небесных тел и вращение Земли) 2. небесную механику (Небесная механика изучает движение небесных тел под действием тяготения, разрабатывает методы определения их орбит, позволяет рассчитать координаты на дальнейшее время (эфемериды), рассматривает движение и устойчивость систем естественных и искусственных небесных тел Раздел небесной механики, связанный с определением орбит и расчётом эфемерид, называют теоретической астрономией) 3. астрофизику (Астрофизика изучает происхождение, строение, химический состав, физические свойства и эволюцию как отдельных тел, так и их систем, вплоть до всей Вселенной в целом. Астрофизика подразделяется на практическую и теоретическую) Основные этапы развития астрономии: · 3 тыс. лет до н.э. (Египет) – по наблюдениям за появлением Сириуса довольно точно была определена продолжительность тропического года · 2 тыс. лет до н.э. (Китай) – видимые движения Солнца и Луны были изучены до такой степени, что можно было предсказывать солнечные и лунные затмения · II век до н.э., Гиппарх (Древняя Греция, Родос) составил первый каталог звёзд и создал геометрическую теорию эпициклов, которая легла в основу геоцентрической системы мира
· II век н.э., Птолемей (Древняя Греция, Александрия) – автор труда «Мегале Синтаксис», или «Альмагест» · В средние века астрономия развивалась в основном в Средней Азии Эпоха великих географических открытий, промышленная революция и Реформация подтолкнули развитие астрономической науки в Европе · Николай Коперник в труде «Об обращениях небесных сфер» (1543) разработал гелиоцентрическую систему мира Иоганн Кеплер установил законы движения планет (1609 – 1618) · Галилео Галилей одним из первых использовал телескоп для астрономических целей (1609), открыл четыре спутника Юпитера (1610) Исаак Ньютон установил основные законы механики, а также закон всемирного тяготения (1686) · XVII – XIX века – открытия новых планет, спутников, астероидов · Середина XIX века и далее – спектральный анализ и фотографирование (в видимом диапазоне) · XX век – астрофизика, СТО, ОТО, современная космология · С 1940-х годов – радиоастрономия · 1957-й – первый искусственный спутник · 1961-й – первый полёт человека в космос · 1969-й – высадка людей на Луну · 1970-е – 1990-е – исследования Марса, Венеры, далёких планет · 1990-е – 2000-е – космический телескоп им. Хаббла (Hubble Space Telescope), открытие планет у других Звёзд Общее представление о масштабах и структуре Вселенной и физическом состоянии вещества · Земля → Солнечная система → Галактика Млечный Путь (150 млрд. звёзд) → Местная группа галактик (более 50 галактик) → Местное сверхскопление галактик (около 30 тыс. галактик) · В общем случае: Звёздная система → Скопление звёзд (10 – 100 тыс. звёзд) → Галактика (1 млрд. – 1 трлн. звёзд) → Местная группа галактик → Местное скопление галактик (1 тыс. – 10 тыс. галактик) → Местное сверхскопление галактик · Скопления галактик располагаются вдоль границ огромных ячеек, подобных пчелиным сотам · С Земли невооружённым взглядом можно наблюдать объекты, в основном принадлежащие нашей Галактике · Среднее расстояние от Земли до Солнца – 150 млн. км, или 1 а.е.
· Орбита Нептуна ~ 30 а.е. · Внешняя граница облака Оорта (граница Солнечной системы) ~ 1 световой год · Расстояние до ближайшей (после Солнца) к нам звезды (α Центавра C, или Проксима) – 1.3 пк (парсека), 1 пк ≈ 3.26 световых года · Наша Галактика состоит из более чем 150 млрд. звёзд и представляет собой «диск» диаметром 100 тысяч световых лет и толщиной 10 тысяч световых лет · Ближайшая галактика – карликовая галактика в созвездии Большого Пса (CMa Dwarf), состоящая всего из 1 млрд. звёзд, находится на расстоянии 25 тысяч световых лет от Солнечной системы · Ближайшая сверхгигантская галактика – Туманность Андромеды. Содержит около 1 трлн. звёзд и находится на расстоянии 2.54 млн. световых лет от Солнечной системы · Самая удалённая галактика – IOK-1 – находится в созвездии Волосы Вероники на расстоянии 12.88 млрд. световых лет. Сформировалась через 750 млн. лет после Большого взрыва · Наблюдаемая часть материи Вселенной в основном сосредоточена в звёздах (~90 %) и межзвёздной среде (~ 10 %) · Часть материи пребывает в форме поля (гравитационного, электромагнитного) · По современным данным, только около 5 % Вселенной составляет обычная барионная (наблюдаемая) материя · Около 23 % приходится на тёмную материю, небарионная компонента которой не участвует в сильном и электромагнитном взаимодействиях · И ещё 72 % составляет «тёмная энергия»
Эклиптика. Эклиптическая система координат. Движение Солнца по эклиптике. Аналемма. Суточное движение Солнца. Изменение со временем положений небесного экватора, эклиптики и точек весеннего и осеннего равноденствий. Эклиптика • Измерения высоты Солнца в полдень (т.е. в момент его верхней кульминации) на одной и той же географической широте показали, что склонение Солнца δŸ в течение года изменяется в пределах от +23026' до –23026', два раза проходя через нуль. • Прямое восхождение Солнца αŸ на протяжении года также постоянно изменяется от 0 до 3600 или от 0 до 24h. • Рассматривая непрерывное изменение обеих координат Солнца, можно установить, что оно перемещается среди звёзд с запада на восток по большому кругу небесной сферы, который называется эклиптикой. • Название эклиптика связано с затмениями (eclipse) Луны или Солнца, т.к. они происходят, когда Луна в день новолуния или полнолуния пересекает круг эклиптики.
Основная плоскость – плоскость эклиптики εϒε'Ω Плоскость эклиптики наклонена к плоскости небесного меридиана под углом ε = 23026' ПП' – ось эклиптики ε – точка летнего солнцестояния ε' – точка зимнего солнцестояния 1) ϒ m = λ (эклиптическая долгота) 2) mM = β (эклиптическая широта)
20-21 марта Солнце находится в точке ϒ, его склонение δŸ = 0 и прямое восхождение αŸ = 0. В этот день (весеннего равноденствия) Солнце восходит точно в точке E и заходит в точке W. Максимальная высота центра Солнца над горизонтом в полдень этого дня (верхняя кульминация): h Ÿ = 900 – φ + δŸ = 900 – φ Затем Солнце сдвинется по эклиптике ближе к точке ε, т.е. δŸ > 0 и αŸ > 0. 21-22 июня Солнце находится в точке ε, его склонение максимально δŸ = 23026', а прямое восхождение αŸ = 6h.
В полдень этого дня (летнего солнцестояния) Солнце поднимается на максимальную высоту над горизонтом: h Ÿ = 900 – φ + 23026' Т.о., в средних широтах Солнце НИКОГДА не бывает в зените Широта Минска φ = 53055' Затем Солнце сдвинется по эклиптике ближе к точке ε, т.е. δŸ начнёт уменьшаться Около 23 сентября Солнце придёт в точку ε, его склонение δŸ = 0, прямое восхождение αŸ = 12h. Этот день (начало астрономической осени) называется днём осеннего равноденствия. 22-23 декабря Солнце окажется в точке ε', его склонение минимально δŸ = – 23026', а прямое восхождение αŸ = 18h. Максимальная высота над горизонтом: h Ÿ = 900 – φ – 23026'
Аналемма – положение Солнца на небе в одно и то же время суток в течение года. Форма аналеммы зависит от двух факторов – угла наклона оси вращения планеты к плоскости эклиптики и формы (степени эллиптичности) орбиты Изменение экваториальных координат Солнца при его движении по эклиптике • Изменение экваториальных координат Солнца в течение года происходит неравномерно. • Склонение изменяется быстрее всего при движении Солнца вблизи точек равноденствий, и медленнее всего – вблизи точек солнцестояний. • Прямое восхождение, наоборот, медленнее изменяется вблизи точек равноденствий, и быстрее – вблизи точек солнцестояний. • Видимое движение Солнца по эклиптике связано с действительным движением Земли по своей орбите вокруг Солнца, а также с тем фактом, что ось вращения Земли не перпендикулярна плоскости её орбиты, а составляет угол ε = 23º26'. • Если бы ε = 0º, то на любой широте в любой день года день был бы равен ночи (без учёта рефракции и размера Солнца). • Полярные дни, длящиеся от 24h до полугода и соответствующие ночи, наблюдаются за полярными кругами, широты которых определяются условиями: φ = ±(90º – ε) = ± 66º34' Изменение со временем положений небесного экватора, эклиптики и точек весеннего и осеннего равноденствий • Положение оси мира и, следовательно, плоскости небесного экватора, а также точек ϒ и Ω не постоянно, а периодически изменяется. • Прецессия – предварение [равноденствий] (лат. praecessio aequinoctiorum). • Вследствие прецессии земной оси ось мира описывает конус вокруг оси эклиптики с углом раствора ~23,50 за 26 000 лет. • Вследствие возмущающего действия планет кривые, описываемые полюсами мира, не замыкаются, а стягиваются в спираль. • Т.к. и плоскость небесного экватора, и плоскость эклиптики медленно изменяют свое положение в пространстве, то точки их пересечения (ϒ и Ω) медленно перемещаются к западу.
• Скорость перемещения (общая годовая прецессия в эклиптике) за год: l = 3600/26 000 = 50,26''. • Общая годовая прецессия в экваторе: m = l cos ε = 46,11''. • В начале нашей эры точка весеннего равноденствия находилась в созвездии Овна, от которого и получила своё обозначение (ϒ), а точка осеннего равноденствия – в созвездии Весов (Ω). С тех пор точка ϒ переместилась в созвездие Рыб, а точка Ω – в созвездие Девы, но их обозначения остались прежними.
Практические задачи астрометрии. Определение всемирного времени. Поправка часов. Ход часов. Определение географической долготы. Определе ние географической широты и поправки часов. Абсолютные и относительные методы измерения экваториальных координат. Практические задачи астрометрии: • Определение точного времени • Определение географических координат пунктов на поверхности Земли • Измерение точных координат светил Определение всемирного времени. Поправка часов. Ход часов. Определение географической долготы Разность между временем T в какой-то момент по стандартной шкале и показаниями рабочих часов T' в этот момент называется поправкой часов u: u = T – T' или T = T' + u Изменение поправки часов за определённый промежуток времени называется ходом часов ω:
С помощью астрономических наблюдений определяется местное звёздное время (s), которое далее пересчитывается в среднее солнечное, т.е. в точное время (T): s = α + t = T = T' + u или u = α + t – T' Если отметить показания часов T' в момент верхней кульминации (t = 0), то u = α – T' Зная поправку часов u, определяют всемирное время (Universal Time, UT). Из сравнения шкал всемирного и атомного времени определяют неравномерность вращения Земли Определение географической долготы λ сводится к вычислению разности местного времени на данном географическом меридиане и времени гринвичского меридиана: λ = Tm – T 0 = u – u 0 Определение географической широты и поправки часов 1) Определение φ и u по измеренным зенитным расстояниям cos z = sin φ sin δ + cos φ cos δ cos t и t = T' + u – α (1) Если для двух (или более) светил, для которых по Астрономическому ежегоднику известны α и δ, измерены z (или h) по звёздным часам в момент времени T', то по (1) можно найти φ и u. 2) Определение φ и u в момент кульминации (t = 0 или 12h) Для верхней кульминации к югу от зенита: φ = δ + z (2) Для верхней кульминации к северу от зенита: φ = δ – z (3) Для нижней кульминации: φ = 1800 – δ – z (4) Т.о., по известному δ и измеренному z из (2) – (4) определяют широту Поправка часов для верхней кульминации: u = α – T' (5) Поправка часов для нижней кульминации: u = α – T' + 12h (6) Абсолютные и относительные методы измерения экваториальных координат. Абсолютный метод определения склонений Измеряются зенитные расстояния (или высоты) незаходящей звезды в верхней и нижней кульминации:
z в.к. = δ –φ и z н.к. = 1800 – φ – δ Откуда: δ = 900 – ½ (z н.к. – z в.к.) и φ= 900 – ½ (z н.к. + z в.к.) Т.е. определена широта места наблюдения и склонение одной звезды. Аналогичным образом находятся φ и δ для нескольких незаходящих звёзд, и значение φ усредняется. Далее по формулам (2) – (4) находятся склонения других звёзд (в т.ч. и заходящих).
Вблизи дней солнцестояний (т.е. когда δŸ принимает экстремальные значения) проводят измерения δŸ, абсолютная величина которого = ε. Далее вычисляется αŸ и s = αŸ = T' Ÿ + u, т.е. поправка часов. Выбираются 30 – 40 ярких звёзд, равномерно расположенных вдоль эклиптики и небесного экватора, и которые можно наблюдать до или после наблюдений Солнца. Такие звёзды называются часовыми. При наблюдении часовых звёзд определяют их моменты прохождения через меридиан (кульминации): T' 1, T' 2, …, T'n. При наблюдении Солнца определяется момент его прохождения через меридиан T' Ÿ и зенитное расстояние в этот момент z Ÿ. Далее вычисляется δŸ и αŸ, а также поправки и ход часов на каждый день наблюдения. Для каждого дня наблюдения составляют уравнения для Солнца и часовых звёзд: αŸ = T' Ÿ + u, α1 = T' 1 + u 1, …, α n = T'n + un. В уравнении для Солнца известны все величины, а в уравнениях для часовых звёзд – величины T'i и поправки часов: ui = u + ω(T'i – T' Ÿ). Т.о. можно определить прямые восхождения звёзд абсолютным методом: α i = T'i + u + ω(T'i – T' Ÿ). В этом методе наблюдения Солнца необходимы для фиксации положения точки ¢ среди звёзд. С этой целью вместо Солнца можно наблюдать любую планету (в т.ч. и малую) Солнечной системы. Относительные методы В относительных методах определение координат сводится к измерению разностей Δδ и Δα определяемых и опорных звёзд: T – Ti = α – α i = Δα i. z – zi = δ – δ i = Δδ i
Теоретическое обеспечение и инструменты практической астрономии. Астрономические каталоги, карты и атласы звёздного неба. Угломерные инструменты: универсальный инструмент, секстант, меридианный круг, зениттелескоп, призменная астролябия. Астрономические каталоги • В астрономических каталогах содержаться средние координаты звезд, т.е. экваториальные координаты после того, как из них вычтены различные поправки (рефракция, аберрация и др.). • Каталоги положений составляются на начало определённого года. На основании каталогов положений составляются фундаментальные каталоги, в которых, кроме экваториальных координат, указывается собственное движение звезды, параллаксы и другие данные. • Первый каталог (более 850 звёзд) был составлен Гиппархом во II веке до н.э. • Общий каталог Босса (General Catalog, GC) был создан Л. Боссом в 1937 г. И содержит 33 342 звёзд до 7 m. • С помощью радиоастрономических наблюдений была создана новая система привязки системы отсчёта небесных координат к очень удалённым, т.е. устойчивым радиоисточникам (International Celestial Reference System, ICRS). • Специальные космические аппараты («Гиппаркос», HIPPARCOS, 1989–1993) позволили измерить с точностью до 0,001" координаты, собственные движения и параллаксы 118 218 объектов (каталог Гиппаркос). Каталог Гиппаркос обеспечивает систему координат ICRS, т.е. привязан к внегалактическим объектам. • В каталоге Тихо содержаться аналогичные данные для более чем 2 000 000 объектов с точностью от 0,007 до 0,025". • Кроме звёздных каталогов, имеются каталоги других небесных объектов • «Каталог туманностей и звёздных скоплений» («Catalogue des Nébuleuses et des Amas d'Étoiles») был составлен Ш. Мессье (Charles Messier) в 1781 г. и включал 103 объекта. Обозначения в этом каталоге: M 31 – Туманность Андромеды • «Новый общий каталог туманностей и звёздных скоплений» («A New General Catalogue of Nebulae and Clusters of Stars, being the Catalogue of the late Sir John F.W. Herschel, Bart., revised, corrected, and enlarged», NGC) составлен Й. Дрейером (John Louis Emil Dreyer) в 1888 г. и содержал данные о 7 840 объектах. К настоящему времени издано два дополнения (IC I и IC II), в которых содержатся данные ещё о 5 386 объектах. Обозначения: NGC 224 – Туманность Андромеды • Существуют каталоги и других небесных объектов – двойных звёзд, рентгеновских и радиоисточников и др. • Астрономические ежегодники Карты и атласы звёздного неба • «Уранография: описание всего звёздного неба» («Uranographia: totum caelum stellatum») — атлас звёздного неба Яна Гевелия (Johannes Hevelius). Издан в 1690 г. • Атлас включает 56 карт. На картах с точностью в одну угловую минуту нанесены 1564 звезды по каталогу Гевелия. Атлас Гевелия достиг точности одного порядка с бумажными картами и атласами нашего времени. Универсальный инструмент • Универсальный инструмент (УИ) – один из основных угломерных инструментов, позволяющий в любой точке земной поверхности измерять горизонтальные координаты светила. • УИ состоит из астрономической трубы, которая может поворачиваться вокруг двух взаимно перпендикулярных осей – горизонтальной и вертикальной. Углы поворота вокруг одной и второй оси отсчитываются по двум кругам (или лимбам) – вертикальному и горизонтальному. • УИ используется почти исключительно как переносный инструмент в различных экспедициях для определения географических координат места наблюдения и азимутов земных предметов. • Если в УИ вертикальный круг разделён более точно, чем горизонтальный, то такой инструмент называется вертикальным кругом. Если наоборот – то теодолитом. Секстант • Секстант (секстан) — это измерительный инструмент, используемый для измерения величины угла между двумя видимыми объектами. • Обычно секстант используется для измерения высоты астрономического объекта над горизонтом с целью Определения географических координат. Меридианный круг • Меридианный круг (МК) состоит из астрономической трубы, которая может вращаться только вокруг горизонтальной оси. Эта ось лежит на жёстко закрепленных основах. • Горизонтальная ось МК должна быть направлена точно с востока на запад. Тогда труба будет располагаться и вращаться точно в плоскости небесного меридиана. • МК позволяет измерять зенитные расстояния светил в момент кульминации, т.е. определять склонения светил. • Если отметить по часам момент кульминации, то с помощью МК можно определить и прямое восхождение Светила Зенит-телескоп • Зенит-телескоп служит для точного измерения малых разностей зенитных расстояний вблизи зенита. • Систематические наблюдения на зенит-телескопах ведутся для определения точных значений географической широты места наблюдения с целью изучения движения полюсов Земли.
Астрономо-геодезический инструмент для определения широты места и поправки часов по наблюдаемым моментам прохождения звёзд в различных азимутах через некоторый альмукантарат, Призменная астролябия может быть использована также для определения экваториальных координат звёзд и планет. Перед объективом 3 горизонтально расположенной астрономической трубы (для компактности оптическая ось трубы изломана с помощью двух зеркал 4 и 5) помещается равносторонняя стеклянная призма 1. Под призмой устанавливается ртутный горизонт 2. Свет от наблюдаемой звезды, падая на верхнюю грань призмы и преломляясь, даёт её изображение в фокальной плоскости объектива; второе изображение этой же звезды получается от её света, проходящего через нижнюю грань призмы после отражения от ртутного горизонта. Вследствие видимого суточного движения звезды оба изображения приближаются друг к другу и совпадают; в момент прохождения звезды через альмукантарат с зенитным расстоянием, близким к 30°, изображения рассматриваются в окуляр 6. Для регистрации момента микрометр инструмента имеет специальную призму Волластона 7, перемещая которую микрометрическим винтом, снабженным контактным барабаном, записывают на хронографе серию моментов, что позволяет повысить точность окончательного результата.
10. Видимые движения планет на фоне звёзд. Системы мира Клавдия Птолемея, Николая Коперника и Тихо Браге. Конфигурации планет. Синодические и сидерические периоды обращения планет. Гелиоцентрические и геоцентрические долготы. Великие противостояния Марса. Парад планет. Видимые движения планет на фоне звёзд • По видимым движениям планеты делятся на две группы – нижние, или внутренние (Меркурий и Венера) и верхние, или внешние (все остальные, кроме Земли). • Нижние планеты не отклоняются далеко от Солнца (Меркурий – на 18-280, Венера – на 45-480). Верхние планеты отходят от Солнца на 1800.
Система мира Птолемея Для объяснения видимых движений Солнца, Луны, звёзд и планет древнегреческий учёный Клавдий Птолемей (около 87–165 н.э.) предложил в труде «Альмагест» геоцентрическую систему мира: 1. Земля шарообразна и находится в центре Вселенной; 2. Земля неподвижна; 3. Все небесные тела движутся вокруг Земли; 4. Движение небесных тел происходит по окружностям с постоянной скоростью. Суточное движение всех светил объяснялось вращением Вселенной как одного целого вокруг неподвижной Земли Система мира Коперника В труде «Об обращениях небесных сфер» (1543) Николай Коперник (1473–1543) разработал гелиоцентрическую систему мира: 1. В центре мира находится Солнце; 2. Шарообразная Земля вращается вокруг своей оси и это вращение объясняет кажущееся суточное движение всех светил; 3. Земля, как и другие планеты, обращается вокруг Солнца по окружности, и это обращение объясняет видимое движение Солнца среди звёзд; 4. Все движения представляются в виде равномерных круговых движений; 5. Кажущиеся прямые и попятные движения планет принадлежат не им, а Земле. В результате анализа наблюдательных данных Коперник пришёл к выводу, что все планеты, в т.ч. и Земля, движутся вокруг Солнца примерно в одной плоскости. Луна движется вокруг Земли и, как спутник, вместе с Землёй – вокруг Солнца. Т.к. Меркурий и Венера (нижние или внутренние планеты) в видимых движениях не отходят далеко от Солнца, то их орбиты расположены ближе к Солнцу, чем орбита Земли. Чем дальше внутренняя планета отходит от Солнца, тем больше радиус её орбиты. Остальные планеты (Марс, Юпитер и Сатурн – верхние или внешние планеты) обращаются вокруг Солнца на более далёком расстоянии, чем Земля. Чем медленнее движется внешняя планета, тем дальше она расположена от Солнца. Система мира Тихо Браге • В конце XVI-го века Тихо Браге предложил свою компромиссную гео-гелиоцентрическую систему мира, которая представляла собой комбинацию учений Птолемея и Коперника: Солнце, Луна и звёзды вращаются вокруг неподвижной Земли, а все планеты и кометы — вокруг Солнца. • С расчётной точки зрения эта модель ничем не отличалась от системы Коперника, однако имела одно важное преимущество, особенно после суда над Галилеем: она не вызывала возражений у инквизиции.
Конфигурации планет C – Солнце, T – Земля V 1 – нижнее соединение, V 2 – верхнее соединение V 3 – западная элонгация, V 4 – восточная элонгация M 1 – противостояние, M 2 – соединение M 3 – западная квадратура, M 4 – восточная квадратура Синодические и сидерические периоды обращения планет • Синодическим периодом обращения (S) планеты называется промежуток времени между двумя её последовательными дноимёнными конфигурациями. • Сидерическим, или звёздным, периодом обращения (T) планеты называется промежуток времени, за который планета совершает один полный оборот вокруг Солнца. • Сидерический период обращения Земли называется звёздным годом (T Δ). • Непосредственно из наблюдений с Земли можно определить только T Δ и синодические периоды планет.
• C – Солнце, • P – внутренняя планета • Т – Земля • L – гелиоцентрическая долгота Земли • l – гелиоцентрическая долгота планеты • λ – геоцентрическая долгота планеты Великие противостояния Марса • Великие противостояния Марса – эпохи наиболее тесного сближения Земли и Марса, предоставляющие астрономам возможность детально исследовать эту планету с помощью телескопов. Великие противостояния наступают регулярно, с промежутком в 15 или 17 лет и в последние столетия неизменно приносят ученым ценные открытия в изучении природы Марса. • Орбита Марса располагается следом за орбитой Земли. Оборот Земли по орбите происходит за год, а Марса – за 686,94 земных суток. • Противостояния Земли и Марса происходят в среднем через 780 суток. В период противостояния Марс близок к Земле и его поверхность удобнее всего изучать в телескоп. Если бы орбиты Земли и Марса были совершенно круглыми и лежали в одной плоскости, то все противостояния этих планет были бы одинаковы. Но орбиты планет немного наклонены друг к другу и эллиптичны. А поскольку время между ротивостояниями немного больше двух лет, то Земля за это время совершает чуть больше двух оборотов по орбите, а Марс – немного больше одного оборота. • Т.о., при каждом противостоянии эти планеты встречаются в разных точках своих орбит, приближаясь друг к другу на разное расстояние. • Если противостояние случается в период зимы (с января по март) то расстояние от Земли до Марса довольно велико, около 100 млн. км. Но если Земля сближается с Марсом в конце лета, когда Марс проходит перигелий своей орбиты, то его расстояние сокращается всего до 56–60 млн. км. Такие благоприятные для астрономических наблюдений противостояния называют великими. Противостояние тем благоприятнее, чем ближе оно приходится к 28 августа, так как в этот день Земля проходит ближе всего к перигелию орбиты Марса. • Самым знаменитым среди великих противостояний Марса считают случившееся в начале сентября 1877. Именно тогда американский астроном А. Холл открыл два спутника Марса – Фобос и Деймос. • Во время предыдущего великого противостояния (28 августа 2003) Марс приблизился к Земле на 55,79 млн. км – минимальное за последние два века расстояние. Следующее великое противостояние Марса произойдёт 27 июля 2018. В этот день расстояние до Марса составит 57,77 млн. км. 11. Основы механики планет и других небесных тел. Законы Кеплера. Параметры и элементы орбит. Прямая и обратная задачи астрономии. Закон всемирного тяготения и его роль в астрономии. Задача двух тел. Законы Кеплера 1. Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце. 2. Радиус-вектор планеты за равные промежутки времени описывает равновеликие площади. 3. Квадраты сидерических (звёздных) периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.
• F 1 и F 2 – фокусы, • O – центр • ПО = ОА = a – большая полуось, • OF 1/ OП = e – эксцентриситет • П – перицентр (ближайшая точка орбиты небесного тела к силовому центру) • А – апоцентр (наиболее удалённая точка орбиты небесного тела от силового центра) • АП – линия апсид • q = a (1 – e) – расстояние планеты от Солнца в перицентре • Q = a (1 + e) – расстояние планеты от Солнца в апоцентре • a = (q + Q)/2 – среднее расстояние планеты от Солнца (большая полуось) Перицентры и апоцентры • В орбитах планет Солнечной системы перицентр и апоцентр называют, соответственно, перигелий и афелий. • В орбитах Луны и искусственных спутников Земли – перигей и апогей. • В орбитах двойных звёзд — периастр и апоастр. • В орбитах спутников других планет — перипланет и апопланет, а также иногда: • периселений и апоселений — относительно Луны, • перигермесий и апогермесий —относительно Меркурия, • перигесперий и апогесперий —относительно Венеры, • периарий и апоарий —относительно Марса, • перийовий и апойовий—относительно Юпитера, • перикроний и апокроний —относительно Сатурна, • периураний и апоураний —относительно Урана, • перипосейдий и апопосейдий —относительно Нептуна, • перигадий и апогадий— относительно Плутона. Эксцентриситеты • Для окружности e = 0 (т.к. OF 1 = 0). • Орбиты планет Солнечной системы мало отличаются от круговых, т.е. эксцентриситеты их орбит невелики. • Наименьший эксцентриситет у орбиты Венеры: e = 0,007. • Наибольший – был у орбиты Плутона (e = 0,249), теперь – у орбиты Меркурия (e = 0,206). • Эксцентриситет орбиты Земли: e = 0,017. Второй закон Кеплера • Площадь сектора F 1 P 1 P 2, описанная радиусом-вектором планеты за время Δ t вблизи перицентра, равна площади сектора F 1 P 3 P 4, описанной им за то же время Δ t вблизи апоцентра. • Т.к. дуга P 1 P 2 больше дуги P 3 P 4, то планета вблизи перицентра имеет скорость большую, чем вблизи апоцентра. • Т.е. движение планеты вокруг Солнца неравномерно.
Третий закон Кеплера • Квадраты сидерических (звёздных) периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит, или
• Если большие полуоси орбит выражать в единицах среднего расстояния Земли от Солнца (в а.е.), а периоды обращения планет – в земных годах, то для Земли a Δ = 1, T Δ = 1, и период обращения любой планеты вокруг Солнца:
Движение планеты вполне определено, если: • известна плоскость, в которой лежит её орбита, • размеры и форма орбиты, \ • ориентирование орбиты в пространстве; • момент времени, в который планета находится в определённой точке пространства. Величины, определяющие орбиту планеты, называются элементами орбиты. За основную плоскость, относительно которой пределяется положение орбиты, принимается плоскость эклиптики. Две точки, в которых орбита планеты пересекается с плоскостью эклиптики, называются узлами – восходящим и нисходящим. Восходящий узел – тот, в котором планета пересекает эклиптику, удаляясь от её южного полюса. Эллиптическую орбиту планеты определяют следующие шесть элементов: 1.Наклонение i плоскости орбиты к плоскости эклиптики, 0 ≤ i ≤ 1800. Если 0 ≤ i ≤ 900, то планета движется вокруг Солнца в том же направлении, что и Земля. 2.Гелиоцентрическая долгота восходящего узла ♌, т.е. угол, отсчитываемый из центра Солнца от направления на ¢ до направления на восходящий узел ♌, 0 ≤ ♌ ≤ 3600. Долгота восходящего узла ♌ и наклонение i определяют положение плоскости орбиты в пространстве и направление движения планеты. 3.Угловое расстояние перицентра от восходящего узла (аргумент перицентра) ω, т.е. угол между направлениями из центра Солнца на восходящий узел ♌ и перицентр П, 0 ≤ ω ≤ 3600. 4.Большая полуось a орбиты, которая при заданной массе однозначно определяет сидерический период обращения планеты. 5.Эксцентриситет орбиты e. 6.Момент прохождения через перицентр t 0. Прямая и обратная задачи астрономии • Основные задачи теоретической астрономии – вычисление эфемерид (прямая задача) и определение орбит (обратная задача). • Определение видимых координат планет по элементам их орбит называется вычислением эфемерид, т.е. положений планет на любые моменты времени. • Определение элементов орбит по координатам, полученным из наблюдений, называется определением орбит. Закон всемирного тяготения и его роль в астрономии
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 2244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.150 (0.208 с.) |
 Эклиптическая СК
Эклиптическая СК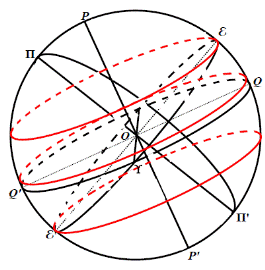 Изменение экваториальных координат Солнца при его движении по эклиптике
Изменение экваториальных координат Солнца при его движении по эклиптике
 Абсолютный метод определения прямых восхождений
Абсолютный метод определения прямых восхождений ε ε' – эклиптика, QQ' – небесный экватор, ε – наклонение эклиптики к экватору (угол между плоскостями), mC – склонение центра Солнца δŸ (дуга на поверхности сферы), ϒ m – прямое восхождение Солнца αŸ. Сферический треугольник ϒ mC – прямоугольный, поэтому:
ε ε' – эклиптика, QQ' – небесный экватор, ε – наклонение эклиптики к экватору (угол между плоскостями), mC – склонение центра Солнца δŸ (дуга на поверхности сферы), ϒ m – прямое восхождение Солнца αŸ. Сферический треугольник ϒ mC – прямоугольный, поэтому: Призменная астролябия
Призменная астролябия • Видимые движения нижних планет происходят следующим образом. В момент наилучшей вечерней видимости Венера находится в восточной элонгации (в наибольшем угловом удалении от Солнца к востоку). Затем Венера движется попятным движением (с востока на запад) и приближается к Солнцу, проходит между Солнцем и Землёй (нижнее соединение). Затем Венера продолжает двигаться попятным движением и достигает западной элонгации (момента наилучшей утренней видимости), где нижняя планета останавливается. Далее планета двигается прямым движением (с запада на восток), проходит за Солнцем (верхнее соединение) и опять достигает восточной элонгации.
• Видимые движения нижних планет происходят следующим образом. В момент наилучшей вечерней видимости Венера находится в восточной элонгации (в наибольшем угловом удалении от Солнца к востоку). Затем Венера движется попятным движением (с востока на запад) и приближается к Солнцу, проходит между Солнцем и Землёй (нижнее соединение). Затем Венера продолжает двигаться попятным движением и достигает западной элонгации (момента наилучшей утренней видимости), где нижняя планета останавливается. Далее планета двигается прямым движением (с запада на восток), проходит за Солнцем (верхнее соединение) и опять достигает восточной элонгации. • Прямое доказательство движения Земли вокруг Солнца появилось только в 1727 году (аберрация света), но фактически система Браге была отвергнута большинством учёных ещё в XVII веке как неоправданно и искусственно усложнённая по сравнению с системой Коперника-Кеплера.
• Прямое доказательство движения Земли вокруг Солнца появилось только в 1727 году (аберрация света), но фактически система Браге была отвергнута большинством учёных ещё в XVII веке как неоправданно и искусственно усложнённая по сравнению с системой Коперника-Кеплера. • Периоды S, T и T Δ связаны уравнением синодического движения: ω = 3600/ T – угловое смещение планеты за сутки ωΔ = 3600/ T Δ – угловое смещение Земли за сутки Δω = |ω – ωΔ| – видимое угловое смещение планеты за сутки
• Периоды S, T и T Δ связаны уравнением синодического движения: ω = 3600/ T – угловое смещение планеты за сутки ωΔ = 3600/ T Δ – угловое смещение Земли за сутки Δω = |ω – ωΔ| – видимое угловое смещение планеты за сутки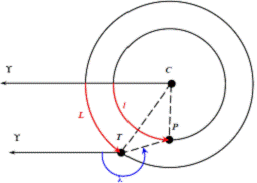 Гелиоцентрические и геоцентрические долготы
Гелиоцентрические и геоцентрические долготы Параметры эллиптической орбиты
Параметры эллиптической орбиты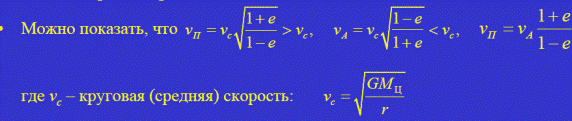


 Элементы орбиты
Элементы орбиты


