
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Небесная сфера. Основные плоскости, линии и точки небесной сферы. Светила, их классификация, видимые движения. Горизонтальная и экваториальные системы координат.Содержание книги
Поиск на нашем сайте
• Под небесной сферой принято понимать сферу произвольного радиуса, центр которой находится в точке наблюдения, и на поверхность этой сферы проецируются все окружающие нас небесные тела или светила • Вращение небесной сферы для наблюдателя, находящегося на поверхности Земли, воспроизводит суточное движение светил на небе Основные плоскости, линии и точки небесной сферы
SWNE – истинный (математический) горизонт, aMa' – альмукантарат, ZMZ' – круг высоты (вертикальный круг), или вертикал
P – северный полюс мира, P' – южный полюс мира, ∠ PON = ϕ (широта места наблюдения), QWQ'E – небесный экватор, bMb' – суточная параллель, PMP' – круг склонения, PZQSP'Z'Q'N – небесный меридиан, NOS – полуденная линия Светила, их классификация, видимые движения Звезды: · Невооружённым взглядом в ясную безлунную ночь в северном полушарии видно около 3 000 звёзд, т. е. всего на небесной сфере видно 6 000 звёзд. · Взаимное положение звёзд друг относительно друга изменяется крайне медленно, и без специальных приборов такое изменение наблюдать не возможно. Т. о., суточное движение звезды по небесной сфере изо дня в день (из ночи в ночь) одно и то же. · Звёзды принято объединять в созвездия. В настоящее время выделяют 88 созвездий. · Самая яркая звезда в созвездии обознается α, далее β, γ, δ и т.д. Для менее ярких звёзд используется числовая нумерация. Около 130 самых ярких звёзд имеют собственные названия: Сириус, Капелла, Вега и др. · На восточной стороне горизонта звёзды восходят, затем поднимаются до некоторой максимальной высоты над горизонтом, после чего опускаются и заходят на западной стороне горизонта. Каждая звезда всегда восходит в одной и той же точке восточной стороны и заходит всегда в одной и той же точке западной. Солнце и Луна: • Солнце и Луна, также, как и звёзды, восходят на восточной стороне горизонта и заходят на западной. Но в разные дни года они восходят в разных точках восточной стороны и заходят тоже в разных точках западной. • Луна смещается с запада на восток примерно на 13º в сутки и совершает полный круг по небу за 27,32 суток, проходя по т.н. зодиакальным созвездиям. • Солнце также перемещается по небу с запада на восток, проходя те же зодиакальные созвездия, смещаясь за сутки примерно на 1º, и совершает весь путь за 1 год.
Планеты: • Ещё в древности были замечены 5 светил, похожих на звёзды, но «блуждающих» по созвездиям. Они были названы планетами – «блуждающими светилами». • Позже были открыты ещё 3 планеты, а затем 1 была «закрыта». • Планеты большую часть времени перемещаются по зодиакальным созвездиям с запада на восток (прямое движение), но часть времени – с востока на запад (попятное движение). Горизонтальная и экваториальные системы координат. • Поскольку радиус небесной сферы произволен, положение светила на небесной сфере однозначно определяется двумя угловыми координатами, если задана основная плоскость и начало отсчёта. • В сферической астрономии используются следующие системы небесных координат (1. Горизонтальная, 2. 1-я экваториальная, 3. 2-я экваториальная, 4. Эклиптическая)
Основная плоскость –плоскость математического горизонта 1) ∠mOM = h (высота) 0 ≤ h ≤ 90 –90 ≤ h ≤ 0 или ∠ZOM = z (зенитное расстояние) 0 ≤ z ≤ 180 z + h = 90 2) ∠SOm = A (азимут) 0 ≤ A ≤ 360
Основная плоскость – плоскость небесного экватора 1) ∠mOM = δ (склонение) 0 ≤ δ ≤ 90 –90 ≤ δ ≤ 0 или ∠POM = p (полюсное расстояние) 0 ≤ p ≤ 180 p + δ = 90 2) ∠QOm = t (часовой угол) 0 ≤ t ≤ 360 или 0h ≤ t ≤ 24h
Системы небесных координат
• Склонение δ не изменяется. • Необходимо ввести вместо t такую экваториальную координату, которая бы отсчитывалась от фиксированной на небесной сфере точки. 2-я экваториальная система координат Основная плоскость – плоскость небесного экватора 1) ∠mOM = δ (склонение) 0 ≤ δ ≤ 90 –90 ≤ δ ≤ 0 или ∠POM = p (полюсное расстояние) 0 ≤ p ≤ 180 p + δ = 90 2) ∠ ϒOm = α (прямое восхождение) 0 ≤α≤ 360 или 0h ≤α≤ 24h
Системы небесных координат • Горизонтальная СК используется для определения направления на светило относительно земных объектов. • 1-я экваториальная СК используется преимущественно при определении точного времени. • 2-я экваториальная СК является общепринятой в астрометрии.
3. Параллактический треугольник и преобразование небесных координат. Восход и заход светил. Верхняя и нижняя кульминации. Моменты времени восхода и захода светил и их азимуты. Сумерки. Белые ночи. Параллактическим треугольником называется сферический треугольник, образованный пересечением небесного меридиана (дуга PZ), вертикала (дуга ZM) и часовым
1) Дуга Qm = t, т.е.∠ZPM = t 2) Сторона PM = 900 – δ, т.к. mM = δ 3) Сторона ZM = z 4) ∠PZM = 1800 – A, т.к. дуга Sm' = A 5) Сторона PZ = 900 – ϕ, т.к. ∠PON = ϕ ∠PMZ = q называется параллактическим углом.
Преобразования координат Используя формулы сферической тригонометрии, для параллактического треугольника можно получить две системы соотношений, связывающих ГСК и ЭСК:
Восход и заход светил. · Вследствие суточного вращения небесной сферы все светила описывают круги, плоскости которых параллельны плоскости небесного экватора, т.е. движутся по суточным параллелям. · · Точка пересечения светилом горизонта при движении снизу вверх называется точкой восхода, сверху вниз – захода
· В случае δ = 900 – ϕ (для северного полушария) суточная параллель касается горизонта в точке севера N. · Условие δ < 900 – ϕ определяет восходящие и заходящие светила. · С учётом южного полушария: |δ| < 900 – |ϕ| Из первой формулы системы (2):
Пренебрегая рефракцией и суточным параллаксом для светила на горизонте (z = 900):
Два решения: t зах = t и t восх = – t. Аналогично из первой формулы системы (1) находятся азимуты точек восхода и захода:
A зах = A и A восх = 3600 – A Кульминации • Суточная параллель светила пересекает небесный меридиан в двух точках. Явление пересечения светилом небесного горизонта называется кульминацией светила. • В верхней кульминации светило имеет максимальную высоту над горизонтом. • В нижней кульминации – минимальную. • Верхняя кульминация может происходить к югу и к северу от зенита.
h Н.К. = δ – (900 – ϕ) или h Н.К. = ϕ + δ – 900
Сумерки Излучение Солнца рассеивается в атмосфере, и поэтому даже после полного захода Солнца (либо перед его восходом наблюдаются сумерки – вечерние (или утренние) • Вечерние гражданские сумерки продолжаются до тех пор, пока высота центра Солнца не станет равной h Ÿ = –6º.
• Утренние гражданские сумерки начинаются перед восходом Солнца, когда высота его центра h Ÿ = –6º. • Навигационные (вечерние и утренние) сумерки длятся в течение времени, пока –6º ≤ h Ÿ < –12º. • За начало или окончание астрономических (вечерних и утренних) сумерек принимается тот момент, когда высота центра Солнца h Ÿ = –18º. Белые ночи • На географической широте ϕ = 60034' в день летнего солнцестояния, когда δŸ = +23026' высота Солнца h Ÿ в нижней кульминации (т.е. в полночь) в соответствии с формулой h Н.К. = ϕ + δ – 900 будет равна – 60. • Т.о., на такой широте в такой день окончание вечерних сумерек совпадёт с началом утренних, т.е. гражданские сумерки длятся всю ночь, которая называется белой. • На широте Минска (φ = 53º55') «гражданские» белые ночи не наступают • Условия для наступления «навигационной» белой ночи практически выполняются в ночь летнего солнцестояния • Задание: определить даты начала и окончания «астрономических» белых ночей на широте Минска
Эклиптика. Эклиптическая система координат. Движение Солнца по эклиптике. Аналемма. Суточное движение Солнца. Изменение со временем положений небесного экватора, эклиптики и точек весеннего и осеннего равноденствий. Эклиптика • Измерения высоты Солнца в полдень (т.е. в момент его верхней кульминации) на одной и той же географической широте показали, что склонение Солнца δŸ в течение года изменяется в пределах от +23026' до –23026', два раза проходя через нуль. • Прямое восхождение Солнца αŸ на протяжении года также постоянно изменяется от 0 до 3600 или от 0 до 24h. • Рассматривая непрерывное изменение обеих координат Солнца, можно установить, что оно перемещается среди звёзд с запада на восток по большому кругу небесной сферы, который называется эклиптикой. • Название эклиптика связано с затмениями (eclipse) Луны или Солнца, т.к. они происходят, когда Луна в день новолуния или полнолуния пересекает круг эклиптики.
Основная плоскость – плоскость эклиптики εϒε'Ω Плоскость эклиптики наклонена к плоскости небесного меридиана под углом ε = 23026' ПП' – ось эклиптики ε – точка летнего солнцестояния ε' – точка зимнего солнцестояния 1) ϒ m = λ (эклиптическая долгота) 2) mM = β (эклиптическая широта)
20-21 марта Солнце находится в точке ϒ, его склонение δŸ = 0 и прямое восхождение αŸ = 0. В этот день (весеннего равноденствия) Солнце восходит точно в точке E и заходит в точке W. Максимальная высота центра Солнца над горизонтом в полдень этого дня (верхняя кульминация): h Ÿ = 900 – φ + δŸ = 900 – φ Затем Солнце сдвинется по эклиптике ближе к точке ε, т.е. δŸ > 0 и αŸ > 0. 21-22 июня Солнце находится в точке ε, его склонение максимально δŸ = 23026', а прямое восхождение αŸ = 6h. В полдень этого дня (летнего солнцестояния) Солнце поднимается на максимальную высоту над горизонтом: h Ÿ = 900 – φ + 23026' Т.о., в средних широтах Солнце НИКОГДА не бывает в зените Широта Минска φ = 53055' Затем Солнце сдвинется по эклиптике ближе к точке ε, т.е. δŸ начнёт уменьшаться Около 23 сентября Солнце придёт в точку ε, его склонение δŸ = 0, прямое восхождение αŸ = 12h. Этот день (начало астрономической осени) называется днём осеннего равноденствия. 22-23 декабря Солнце окажется в точке ε', его склонение минимально δŸ = – 23026', а прямое восхождение αŸ = 18h. Максимальная высота над горизонтом: h Ÿ = 900 – φ – 23026'
Аналемма – положение Солнца на небе в одно и то же время суток в течение года. Форма аналеммы зависит от двух факторов – угла наклона оси вращения планеты к плоскости эклиптики и формы (степени эллиптичности) орбиты Изменение экваториальных координат Солнца при его движении по эклиптике • Изменение экваториальных координат Солнца в течение года происходит неравномерно. • Склонение изменяется быстрее всего при движении Солнца вблизи точек равноденствий, и медленнее всего – вблизи точек солнцестояний. • Прямое восхождение, наоборот, медленнее изменяется вблизи точек равноденствий, и быстрее – вблизи точек солнцестояний. • Видимое движение Солнца по эклиптике связано с действительным движением Земли по своей орбите вокруг Солнца, а также с тем фактом, что ось вращения Земли не перпендикулярна плоскости её орбиты, а составляет угол ε = 23º26'. • Если бы ε = 0º, то на любой широте в любой день года день был бы равен ночи (без учёта рефракции и размера Солнца). • Полярные дни, длящиеся от 24h до полугода и соответствующие ночи, наблюдаются за полярными кругами, широты которых определяются условиями: φ = ±(90º – ε) = ± 66º34' Изменение со временем положений небесного экватора, эклиптики и точек весеннего и осеннего равноденствий • Положение оси мира и, следовательно, плоскости небесного экватора, а также точек ϒ и Ω не постоянно, а периодически изменяется. • Прецессия – предварение [равноденствий] (лат. praecessio aequinoctiorum). • Вследствие прецессии земной оси ось мира описывает конус вокруг оси эклиптики с углом раствора ~23,50 за 26 000 лет. • Вследствие возмущающего действия планет кривые, описываемые полюсами мира, не замыкаются, а стягиваются в спираль. • Т.к. и плоскость небесного экватора, и плоскость эклиптики медленно изменяют свое положение в пространстве, то точки их пересечения (ϒ и Ω) медленно перемещаются к западу. • Скорость перемещения (общая годовая прецессия в эклиптике) за год: l = 3600/26 000 = 50,26''. • Общая годовая прецессия в экваторе: m = l cos ε = 46,11''. • В начале нашей эры точка весеннего равноденствия находилась в созвездии Овна, от которого и получила своё обозначение (ϒ), а точка осеннего равноденствия – в созвездии Весов (Ω). С тех пор точка ϒ переместилась в созвездие Рыб, а точка Ω – в созвездие Девы, но их обозначения остались прежними.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.220 (0.011 с.) |

 ZOZ'– отвесная (вертикальная) линия,
ZOZ'– отвесная (вертикальная) линия, POP'– ось вращения небесной сферы (ось мира),
POP'– ось вращения небесной сферы (ось мира), Горизонтальная система координат
Горизонтальная система координат 1-я экваториальная система координат
1-я экваториальная система координат • Все горизонтальные координаты (h, z, A) и часовой угол t первой экваториальной СК непрерывно изменяются в процессе суточного вращения небесной сферы.
• Все горизонтальные координаты (h, z, A) и часовой угол t первой экваториальной СК непрерывно изменяются в процессе суточного вращения небесной сферы. кругом (дуга PM). Этот треугольник связывает координаты ЭСК и ГСК:
кругом (дуга PM). Этот треугольник связывает координаты ЭСК и ГСК:
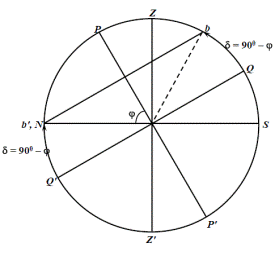 В зависимости от географической широты места наблюдения ϕ и склонения светила δ суточные параллели либо пересекают математический горизонт в двух точках, либо целиком располагаются над ним, либо под ним. (Первые светила – восходящие и заходящие; Вторые – незаходящие; Третьи – невосходящие)
В зависимости от географической широты места наблюдения ϕ и склонения светила δ суточные параллели либо пересекают математический горизонт в двух точках, либо целиком располагаются над ним, либо под ним. (Первые светила – восходящие и заходящие; Вторые – незаходящие; Третьи – невосходящие)


 h В.К. = 900 – ϕ + δ
h В.К. = 900 – ϕ + δ • Угловой диаметр Солнца d Ÿ = 32'
• Угловой диаметр Солнца d Ÿ = 32' Эклиптическая СК
Эклиптическая СК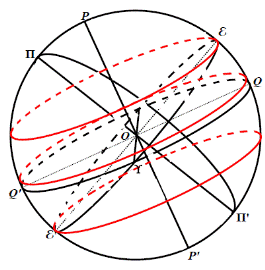 Изменение экваториальных координат Солнца при его движении по эклиптике
Изменение экваториальных координат Солнца при его движении по эклиптике


