Стандартные функции сложного процента для расчета денежных потоков

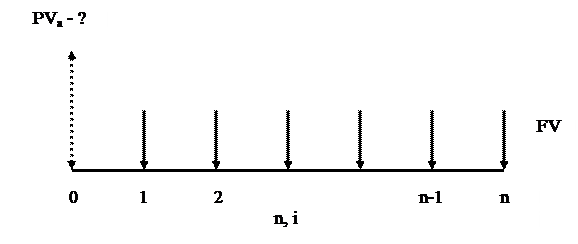
Настоящая стоимость единицы (present value reversion of 1) — данная функция соответствует текущей (на момент оценки) стоимости одной денежной единицы, получаемой через п периодов при i процентах, рис. 2. Направленная вверх стрелка означает получение инвестором суммы денег, а вниз - отдачу. То есть, если инвестор планирует получить через п периодов некоторую сумму (S), следовательно, сегодня ему надо отдать сумму, равную P. Направление стрелок может поменяться: сегодня можно взять у кредитора некоторую сумму (P), которую требуется найти, чтобы через п периодов отдать ему известную сумму, равную S .

Например: Какую сумму следует сегодня положить на счет под 10% на 10 лет, чтобы в будущем получить 1 у.е. Решение: применим формулу (2):

В практике для расчета используют таблицы сложных процентов или электронные таблицы MS Excel.

Любые формулы Excel начинаются со знака равенства. Без знака равенства вводимые данные интерпретируются как текст или число. Ячейка, в которую вводятся данные (формула - это один из видов данных), называется активной. После того как формула введена (нажимается клавиша «Enter»), в активной ячейке появляется значение, вычисленное по введенной формуле, а саму формулу можно увидеть в строке формул (рис. 1).

Порядок вычисления (приоритет) по формуле традиционен для языков программирования:

Ø выражение в скобках вычисляются в первую очередь;

Ø умножение и деление выполняются до сложения и вычитания;

Ø операции одного приоритета выполняются слева направо. Для изменения порядка вычислений используют круглые скобки.

Рис. 3

Ссылки на ячейку можно вводить вручную и с помощью мыши, щелкнув ячейку. После щелчка вокруг ячейки появляется бегущая рамка, а адрес ячейки записывается в формулу. Использование мыши уменьшает количество ошибок и экономит время ввода.

Для расчета стоимости денег во времени в электронных таблицах Excel существуют специальные финансовые функции. Для вызова функции последовательно выбираются следующие пункты меню:

«Вставка» → «Функция», или выбирается на стандартной панели значок fx.

После нажатия кнопки «Enter» или левой кнопки мыши появляется диалоговое окно. Например, для расчета настоящей стоимости Р, используется функция ПС, выбираем ее из предложенного списка.

Рис. 4

После нажатия кнопки «ОК» появляется новое диалоговое окно, в которое вводятся исходные данные (рис. 5).

Рис. 5

После нажатия кнопки «ОК» результат переносится в ячейку. Тот же результат можно получить, введя в ячейку В5 формулу:

ПЗ (В2; В3:: В4) или =ПЗ (0,1;10;;1)

Вызов остальных функций осуществляется аналогично.

Глава 2 Модели финансовых потоков

Основные понятия

 

Аннуитет (финансовая рента) — это ряд последовательных плате­жей через одинаковые промежутки времени. Регулярные взносы в пенсионный фонд — это при­мер аннуитета.

Коэффициент настоящей стоимости аннуитета рассчитывается по формуле:

Интервал ренты — это время между двумя последовательными пла­тежами. Если все платежи равны между собой, то это постоянная рен­та, иначе — переменная рента.

Рис. 6.

Существуют ренты постнумерандо (все платежи осуществляются в конце интервалов ренты) и пренумерандо (все платежи осуществля­ются в начале интервалов ренты). Иногда ренты пренумерандо назы­вают приведенными.

Для расчета наращения или дисконтирования платежей исполь­зуется сложная процентная ставка i.

Наращенная (будущая) сумма ренты S — это все платежи вместе с процентами на дату последней выплаты.

Современная (приведенная) стоимость ренты — это все платежи вместе c процентами, пересчитанные на начальный момент времени ренты с помощью операции математического дисконтирования.

Существуют ренты верные (выплата не ограничена никакими условиями) и условные (выплата обусловлена наступлением какого-то события). Страховые взносы — это пример условной ренты. Срок реализации отложенных рент откладывается на некоторое время.

Пусть р — число рентных платежей в году, а число m показывает, сколько раз в году начисляются проценты. Ренты, для которых р = m, называются простыми. Ренты, для которых р≠ m, называются общими.

Настоящей стоимости аннуитета соответствует функция ПЗ (норма; кпер; выплата;; тип), где i - норма, n – кпер, платеж - выплата - будущая стоимость - бс, тип - по умолчанию 0, что означает, выплата производится в конце периода, тип =1 - выплата в начале периода (авансовые платежи).

На рисунке авансовый платеж показан в виде пунктирной стрелки. Авансовый платеж означает, что всего платежей останется п, но по времени они сдвинутся на один период. Первый платеж будет в «нулевой период» (в текущий момент, его не надо переводить в текущую стоимость), а последний платеж будет выплачен в (n-1)-м периоде (то есть на схеме если есть пунктирная стрелка, то будет отсутствовать последняя стрелка в n-й период).

Пример: если в течение 10 лет фирма каждый год выплачивала 1 у.е., то какая сумма была взята в кредит.

Решение: по формуле:

или =ПС (10%:10:-1;:0) в конце периода. Ответ: 6,14 у.е.;

если в условии было бы сказано, что фирма выплачивала в течение 10 лет в начале каждого года 1 у.е., то решение выглядело бы так:

(«+1» - это авансовый платеж в нулевой период) или =ПС(10%;10;-1;;1) (тип 1 - в начале периода). Ответ: 6,76 у.е.

Для пересчета уже полученных выгод в будущую стоимость используют две функции: будущую стоимость единицы и будущую стоимость аннуитета.

Будущая стоимость единицы (amount of 1 at compound interest) — это функция, определяющая величину будущей стоимости денежной единицы через п периодов при сложном проценте, равном i.

Коэффициент будущей стоимости единицы рассчитывается по формуле:

где i — величина сложного процента:

n — количество периодов начисления сложного процента.

В электронных таблицах Excel функция:

БЗ (норма; кпер;; нз;), где i - норма, n - кпер, текущая стоимость - нз. Например, если сегодня положить в банк 1 у.е. под 10%, то, сколько можно получить через 10 лет.

Решение:

=БЗ(10%;10;;-1;0) или = 1 у.е.×(1+0,1)¹⁰ Ответ: 2,5937 у.е.

Будущая стоимость аннуитета показывает, какова будущая стоимость единичного аннуитета при заданном числе периодов n и норме процента i. Коэффициент будущей стоимости аннуитета рассчитывается по формуле:

 

Рис. 7.

В электронных таблицах Excel функция: БЗ (норма; кпер; выплата;; тип), где i - норма, n – кпер, платеж - выплата, текущая стоимость - нз, тип - по умолчанию 0, то есть выплата производится в конце периода, если тип равен 1, то выплата - в начале периода (авансовые платежи), на рис. 8, авансовый платеж показан пунктирной стрелкой.

Например: если каждый год откладывать 1 у.е. на счет под 10%, то какая сумма будет через 10 лет. Решение:

=БЗ(10%;10;-1;;0) в конце периода, ответ: 15,94 у.е.

=БЗ(10%;10;-1;;1) в начале периода, ответ: 17,53 у.е.

Фактор фонда возмещения, определяющая величину платежа для аннуитета, будущая стоимость которого через n периодов при заданной норме процента равна 1.

Рис. 8.

Например, собственник здания знает, что на ремонт кровли уйдет 1000 у.е., нормативный срок службы данного конструктивного элемента 15 лет, требуется определить, какую сумму следует ежегодно откладывать собственнику в банк, чтобы через 15 лет накопить сумму на ремонт, если ставка банка равна 18%.

Решение:

Для данного примера, фактор фонда возмещения будет равен:

тогда, сумма, которую необходимо ежегодно отгадывать собственнику, будет равна 0,0164×1000=16,4 у.е.

В электронных таблицах Excel: ППЛАТ (норма; кпер;; бс; тип), где i - норма, n - кпер. будущая стоимость - бс, тип - по умолчанию равен 0, то есть выплата производится в конце периода, если тип равен 1, то выплата - в начале периода (авансовые платежи).

Для вышеприведенного примера, периодический платеж будет равен =ППЛАТ(18%; 15;; 1000:0) для выплат в конце периода, ответ: -16.4 у.е.

Рассмотрим основные характеристики самоамортизирующихся кредитов с постоянной нормой процента.

Например, требуется определить величину ежегодной выплаты для самоамортизирующего кредита, суммой 3170 у.е.. взятого на 4 года, под 10 % годовых.

Для расчета платежа по кредиту воспользуемся формулой взноса на амортизацию единицы, которая показывает, каков должен быть размер платежей в течение п периодов, чтобы их настоящая стоимость при норме процента i была равна 1.

Например, для выше приведенного примера взнос на амортизацию единицы равен:

тогда платеж по кредиту будет 3170×0.3155 = 1000 у.е.

В электронных таблицах Excel: ППЛАТ (норма; кпер;нс;; тип), где i - норма, n -кпер. настоящая стоимость – нc, тип - по умолчанию равен 0, то есть выплата производится в конце периода, если тип равен 1, то выплата - в начале периода (авансовые платежи).

Если расчетный период меньше года, то норма процента i должна быть отнесена к количеству периодов в году i/m, а количество лет n увеличено в m раз (nm), где:

m =2 - для полугодового начисления процентов;

m =4 - для ежеквартального начисления процентов:

m=12 - для ежемесячного начисление процентов;

m = 365 - для ежедневного начисления процентов.

Чем больше число начислений в году, тем большая сумма будет накоплена, см. таблицу 2.1.

Таблица 2.1