Глава 1 стоимость денег во времени

Е. А. Боркова

СТРАТЕГИЧЕСКОЕ ПЛАНИРОВАНИЕ –

Задачи и решения

практикум

 

 

Специальность 080103 – Национальная экономика

Направление 080100 - Экономика

 

 

Санкт-Петербург

 

УДК 005.511

ББК 65.290-2

П 82

Утверждено

редакционно-издательским советом СПбГИЭУ

Рецензенты:

 

А.И. Стешин, д.э.н., профессор, зав. кафедрой «Менеджмент организации» БГТУ «Военмех» им. Д.Ф. Устинова.

 

З.А. Сизенова, к.э.н. доцент, Санкт-Петербургского государственного университета экономики и финансов.

 

 

Боркова Е. А.

Стратегическое планирование - Задачи и решения: практикум. СПб.: СПбГИЭУ, 2009. – 116 с.

В учебно-практическом пособии раскрываются основы системного подхода к процессу бизнес-планирования как многофункциональному инструменту управления.

Рассматриваются методы, варианты, общие и частные случаи бизнес-планирования. Приведены экономические, финансово-кредитные, организационно-управленческие задачи, встречающиеся в бизнес-планировании.

Предназначено для студентов, обучающихся по специальности 080103 – Национальная экономика, по направлению 080100 – Экономика.

 

 

© СПбГИЭУ, 2009

Введение

Логика развития и динамика современного рынка ясно свидетельствуют – ни один успешный предприниматель уже не может обойтись без плана развития своего бизнеса. Причем этот план, просто обязан быть составлен на высоком профессиональном уровне. Без детального бизнес-планирования не обойтись не только на этапе создания своего дела, но и на стадиях продвижения товара или услуги на рынок, расширения бизнеса, при выходе на новые рынки, а также в случае реорганизации компаний и производств, осуществлении инвестиционных проектов.

Прежде чем начать какое-либо дело, человек должен тщательно продумать, что именно, к какому сроку, какими способами и с помощью каких средств он должен сделать. В противном случае его намерения могут оказаться невыполненными. Бизнес-планирование позволяет не только обосновать необходимость разработки того или иного инвестиционного проекта, но и возможность его реализации в действующих рыночных условиях.

Цель этого учебно-практического пособия – изложить студентам основные, повсеместно используемые приемы и методы бизнес-планирования, а также объяснить, как и когда следует применять эти приемы и методы, чтобы получить осмысленные решения и ответы.

Весь материал разбит на главы, а главы на параграфы. Каждый параграф – это отдельная тема. В начале параграфа приводится необходимый минимум теоретических сведений, затем подробно разбираются модельные примеры. Показано, как с помощью встроенных функций и надстройки «Пакета анализа» пакета Excel можно избежать долгих и утомительных вычислений. После каждого примера приводится задача для самостоятельного решения.

Структура практикума в соответствии с поставленными задачами включает следующие темы:

1. Стоимость денег во времени.

2. Модели финансовых потоков.

3. Амортизация

4. Методы оценки инвестиций в условиях определенности.

5. Налогообложение и инвестиционные решения.

6. Учет инфляционного обесценения денег

7. Лизинг

8. Зарубежные инвестиции

9. Применение математического ожидания и стандартного отклонения для оценки риска

10. Облигации

Глава 1 Стоимость денег во времени

Английская, немецкая и французская практика начисления процентов

В формуле S = Р(1 + ni) период начисления n измеряется в годах. Это не всегда удобно, так как период начисления может быть меньше года (например, с 18 марта 2007 года по 20 октября 2007 года). В этом случае полагают

n = t/K, где t — период начисления (в днях),

К — продолжительность года (в днях).

Тогда S= P(1 + it/К). Дата вы­дачи и дата погашения ссуды всегда считаются за один день.

В немецкой практике начисления процентов один полный месяц равен 30 дням, продолжительность года К = 360 дней.

Во французской практике период начисления процентов равен фактическому сроку, продолжительность года К= 360 дней.

В английской практике период начисления процентов равен фак­тическому сроку, продолжительность года К = 365 дней (невисокос­ный год) или 366 дней (високосный год).

Пример. Первоначальная сумма Р= 3000 руб. помещена в банк под i = 12% годовых (проценты простые) на срок с 18 марта 2007 года по 20 октября 2007.года. Найти наращенную сумму в немецкой, французской и английской практике начисления процентов.

В немецкой практике начисления процентов продолжительность года К = 360 дней, t = 14 (март) + 6×30 (апрель, май, июнь, июль, август, сентябрь) + 20 (октябрь) – 1 (день открытия и день закрытия счета всегда считается за один день) = 213 дней. Тогда S= P(1 + it/К) = 3000×(1+0,12×213/360) = 3213 руб.

Во французской практике продолжительность года К = 360 дней, t = 14 (март) + 30 (апрель) + 31 (май) + 30 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 20 (октябрь) – 1 (день открытия и день закрытия счета всегда считается за один день) = 216 дней. Тогда S= P(1 + it/К) = 3000×(1+0,12×216/360) = 3216 руб.

В английской практике продолжительность года К = 365 дней, t = 216 дней. Тогда S= P(1 + it/К) = 3000×(1+0,12×216/365) = 3213,04 руб.

Задача 8. Первоначальная сумма Р= 2000 руб. помещена в банк под i = 15% годовых (проценты простые) на срок с 19 февраля 2007 го­да по 27 ноября 2007 года. Найти наращенную сумму в каждой из практик начисления процентов.

Глава 2 Модели финансовых потоков

Основные понятия

 

Аннуитет (финансовая рента) — это ряд последовательных плате­жей через одинаковые промежутки времени. Регулярные взносы в пенсионный фонд — это при­мер аннуитета.

Коэффициент настоящей стоимости аннуитета рассчитывается по формуле:

Интервал ренты — это время между двумя последовательными пла­тежами. Если все платежи равны между собой, то это постоянная рен­та, иначе — переменная рента.

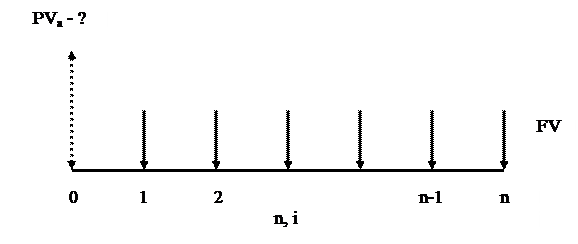
Рис. 6.

Существуют ренты постнумерандо (все платежи осуществляются в конце интервалов ренты) и пренумерандо (все платежи осуществля­ются в начале интервалов ренты). Иногда ренты пренумерандо назы­вают приведенными.

Для расчета наращения или дисконтирования платежей исполь­зуется сложная процентная ставка i.

Наращенная (будущая) сумма ренты S — это все платежи вместе с процентами на дату последней выплаты.

Современная (приведенная) стоимость ренты — это все платежи вместе c процентами, пересчитанные на начальный момент времени ренты с помощью операции математического дисконтирования.

Существуют ренты верные (выплата не ограничена никакими условиями) и условные (выплата обусловлена наступлением какого-то события). Страховые взносы — это пример условной ренты. Срок реализации отложенных рент откладывается на некоторое время.

Пусть р — число рентных платежей в году, а число m показывает, сколько раз в году начисляются проценты. Ренты, для которых р = m, называются простыми. Ренты, для которых р≠ m, называются общими.

Настоящей стоимости аннуитета соответствует функция ПЗ (норма; кпер; выплата;; тип), где i - норма, n – кпер, платеж - выплата - будущая стоимость - бс, тип - по умолчанию 0, что означает, выплата производится в конце периода, тип =1 - выплата в начале периода (авансовые платежи).

На рисунке авансовый платеж показан в виде пунктирной стрелки. Авансовый платеж означает, что всего платежей останется п, но по времени они сдвинутся на один период. Первый платеж будет в «нулевой период» (в текущий момент, его не надо переводить в текущую стоимость), а последний платеж будет выплачен в (n-1)-м периоде (то есть на схеме если есть пунктирная стрелка, то будет отсутствовать последняя стрелка в n-й период).

Пример: если в течение 10 лет фирма каждый год выплачивала 1 у.е., то какая сумма была взята в кредит.

Решение: по формуле:

или =ПС (10%:10:-1;:0) в конце периода. Ответ: 6,14 у.е.;

если в условии было бы сказано, что фирма выплачивала в течение 10 лет в начале каждого года 1 у.е., то решение выглядело бы так:

(«+1» - это авансовый платеж в нулевой период) или =ПС(10%;10;-1;;1) (тип 1 - в начале периода). Ответ: 6,76 у.е.

Для пересчета уже полученных выгод в будущую стоимость используют две функции: будущую стоимость единицы и будущую стоимость аннуитета.

Будущая стоимость единицы (amount of 1 at compound interest) — это функция, определяющая величину будущей стоимости денежной единицы через п периодов при сложном проценте, равном i.

Коэффициент будущей стоимости единицы рассчитывается по формуле:

где i — величина сложного процента:

n — количество периодов начисления сложного процента.

В электронных таблицах Excel функция:

БЗ (норма; кпер;; нз;), где i - норма, n - кпер, текущая стоимость - нз. Например, если сегодня положить в банк 1 у.е. под 10%, то, сколько можно получить через 10 лет.

Решение:

=БЗ(10%;10;;-1;0) или = 1 у.е.×(1+0,1)¹⁰ Ответ: 2,5937 у.е.

Будущая стоимость аннуитета показывает, какова будущая стоимость единичного аннуитета при заданном числе периодов n и норме процента i. Коэффициент будущей стоимости аннуитета рассчитывается по формуле:

 

Рис. 7.

В электронных таблицах Excel функция: БЗ (норма; кпер; выплата;; тип), где i - норма, n – кпер, платеж - выплата, текущая стоимость - нз, тип - по умолчанию 0, то есть выплата производится в конце периода, если тип равен 1, то выплата - в начале периода (авансовые платежи), на рис. 8, авансовый платеж показан пунктирной стрелкой.

Например: если каждый год откладывать 1 у.е. на счет под 10%, то какая сумма будет через 10 лет. Решение:

=БЗ(10%;10;-1;;0) в конце периода, ответ: 15,94 у.е.

=БЗ(10%;10;-1;;1) в начале периода, ответ: 17,53 у.е.

Фактор фонда возмещения, определяющая величину платежа для аннуитета, будущая стоимость которого через n периодов при заданной норме процента равна 1.

Рис. 8.

Например, собственник здания знает, что на ремонт кровли уйдет 1000 у.е., нормативный срок службы данного конструктивного элемента 15 лет, требуется определить, какую сумму следует ежегодно откладывать собственнику в банк, чтобы через 15 лет накопить сумму на ремонт, если ставка банка равна 18%.

Решение:

Для данного примера, фактор фонда возмещения будет равен:

тогда, сумма, которую необходимо ежегодно отгадывать собственнику, будет равна 0,0164×1000=16,4 у.е.

В электронных таблицах Excel: ППЛАТ (норма; кпер;; бс; тип), где i - норма, n - кпер. будущая стоимость - бс, тип - по умолчанию равен 0, то есть выплата производится в конце периода, если тип равен 1, то выплата - в начале периода (авансовые платежи).

Для вышеприведенного примера, периодический платеж будет равен =ППЛАТ(18%; 15;; 1000:0) для выплат в конце периода, ответ: -16.4 у.е.

Рассмотрим основные характеристики самоамортизирующихся кредитов с постоянной нормой процента.

Например, требуется определить величину ежегодной выплаты для самоамортизирующего кредита, суммой 3170 у.е.. взятого на 4 года, под 10 % годовых.

Для расчета платежа по кредиту воспользуемся формулой взноса на амортизацию единицы, которая показывает, каков должен быть размер платежей в течение п периодов, чтобы их настоящая стоимость при норме процента i была равна 1.

Например, для выше приведенного примера взнос на амортизацию единицы равен:

тогда платеж по кредиту будет 3170×0.3155 = 1000 у.е.

В электронных таблицах Excel: ППЛАТ (норма; кпер;нс;; тип), где i - норма, n -кпер. настоящая стоимость – нc, тип - по умолчанию равен 0, то есть выплата производится в конце периода, если тип равен 1, то выплата - в начале периода (авансовые платежи).

Если расчетный период меньше года, то норма процента i должна быть отнесена к количеству периодов в году i/m, а количество лет n увеличено в m раз (nm), где:

m =2 - для полугодового начисления процентов;

m =4 - для ежеквартального начисления процентов:

m=12 - для ежемесячного начисление процентов;

m = 365 - для ежедневного начисления процентов.

Чем больше число начислений в году, тем большая сумма будет накоплена, см. таблицу 2.1.

Таблица 2.1

Начисления (m)	Норма (i)	Кол-во периодов(nm)	БСЕ
Ежегодные (m=1)	10%		2,594
Ежеквартальные (m=4)	10%/ 4	10*4	2.685
Ежемесячные (m=12)	10%/12	10*12	2.707

Дополнительные функции

1. Количество периодов. Для определения количества периодов (n), можно воспользоваться функцией КПЕР (норма; выплата; нз; бс; тип).

Например, если каждый год вносить по 1000 у.е., то через какой период на счету будет 16000 у.е., если ставка 10%. Решение: =КПЕР(10%;-1000;; 16000)= 10 лет. Например, если сегодня положить 10000 рублей, то через, сколько лет сумма увеличиться вдвое, при ставке 10%. Решение: =КПЕР(10%;:-10000;20000)= 7,3 лет.

2. Норма. Для определения i - нормы (ставки, внутренней нормы отдачи[1]) при равных выплатах, можно воспользоваться функцией HOPМA (кпер; выплата; нз, бс; тип). Например, под какой процент нужно вложить 10000 у.е, чтобы через 7 лет получить 20000 у.е. НОРМА(7;;-10000;20000)= 10.4%

Для определения i - нормы (ставки, внутренняя норма отдачи) при неравных выплатах можно воспользоваться функцией ВНДОХ (значения), где значения - это массив или ссылка на ячейки, содержащие числовые величины, для которых вычисляется норма. Значения должны включать, по крайней мере, одно положительное значение и одно отрицательное значение, для того, чтобы можно было вычислить ставку.

Например, чистый операционный доход первого года будет равен 100 тыс. у.е., и будет увеличиваться на 2 тыс. у.е. в год, после 4 лет эксплуатации объект будет продан за 1000 тыс. у.е., вычислить внутреннюю норму отдачи для проекта, если требуются начальные инвестиции в сумме 800 тыс. у.е.

Создаем массив денежных потоков:

в момент времени 0 - -800;

в момент времени 1 - 100;

в момент времени 2 - 102;

в момент времени 3 - 104;

в момент времени 4 - 106+1000.

и вводим весь массив в функцию, см. рис. 9.

Рис. 9.

3. Текущая стоимость неравномерного потока. Функция НПЗ (норма; значение1; значение2;…), где норма - ставка процента, значение1 - доход (выплата, платеж) первого года; значение2 - доход (выплата, платеж) второго года и т.д. данную функцию часто используют для расчета NPV.

Чистая текущая стоимость (NPV) - дисконтированная стоимость всех будущих денежных потоков, минус начальные инвестиции.

где С₀ - начальные инвестиции,

I- ежегодный доход (например, N0I),

Vn - доход от продажи объекта (реверсии).

Например, чистый операционный доход первого года будет равен 100 тыс. у.е., и будет увеличиваться на 2 тыс. у.е. в год. после 4 лет эксплуатации объект будет продан за 1000 тыс. у.е.. найти чистую текущую стоимость проекта, если требуются начальные инвестиции в сумме 800 тыс. у.е.. а норма дисконтирования 10%.

Для определения NPV можно воспользоваться функцией НПЗ, для этого создается массив положительных денежных потоков (100; 102; 104; 1106) и, имея ставку дисконтирования, можно найти текущую стоимость: НПЗ (0,1; 100;102; 104; 1106) =1009 тыс. у.е., см. рис. 10.

Рис. 10.

Тогда NPV= 1009-800=209 тыс. у.е.

Внимание! В справке Excel ошибка: для расчета NPV предлагается

НПЗ (0,1; -800; 100; 102; 104; 1106) = 190, что не совпадает расчету по формуле

NPV=-800+100/(1+0,1)+102/(1+0,1)^2+104/(1+0,1)^3+1106/(1 +0,1)^4=209).

Соответствие финансовых функций EXCEL ХР и EXCEL 98,2000

Таблица 2.3

EXCEL ХР	EXCEL 98, 2000
ПС	ПЗ
БС	БЗ
ПЛТ	ППЛАТ
ЧПС	НПЗ
ВСД	ВНДОХ
СТАВКА	НОРМА

Глава 3 Амортизация

Методы начисления износа

 

При оценке внеоборотных активов возникают те же проблемы, что и при оценке запасов. Как распределить стоимость внеоборотно­го актива на весь период его эксплуатации?

Амортизация — это распределение первоначальной стоимости внеоборотного актива на период его эксплуатации способом, учиты­вающим остаточную стоимость этого актива.

Существуют два основных метода расчета амортизации:

· равномерное начисление износа;

· начисление износа с сокращающейся балансовой стоимости. Рассмотрим основные методы расчета амортизации подробнее.

Метод суммы годичных чисел

Если остаточная стоимость Р = 0, то метод начисления износа с сокращающейся балансовой стоимости использовать нельзя. В этом случае для начисления ускоренной амортизации можно при­менить метод суммы годичных чисел — метод ускоренной амортиза­ции со списанием суммы, равной долям оставшихся лет в общей сум­ме лет.

Задача 18. Пусть в задаче 1 остаточная стоимость Р = 0. Оп­ределим методом суммы годичных чисел ежегодные начисления на износ и балансовую стоимость станка на конец каждого года.

Так как станок используется 4 года, то сумма годичных чисел равна 4 + 3 + 2 + 1 = 10. Поэтому в 1-й, 2-й, 3-й и 4-й годы сумма амортиза­ционных отчислений равна 4/10, 3/10, 2/10 и 1/10 от первоначальной стоимости станка (29000 руб.). Заполним таблицу.

 

 

Год	Перво­начальная стоимость, руб.	Начисления на износ на счете прибылей и убытков, руб.	Накопленная амортизация, руб.	Балансовая стоимость на конец года, руб.

Задача 19. Пусть в задаче 2 остаточная стоимость Р = 0. Опре­делить методом суммы годичных чисел ежегодные начисления на из­нос и балансовую стоимость станка на конец каждого года.

Метод окупаемости

Достоинство метода окупаемости — его простота. На практике этот метод применяется довольно часто, хотя при этом не учитывает­ся временная стоимость денег.

Нужно определить период окупаемости, который показывает, сколько времени понадобится для того, чтобы инвестиционный про­ект окупил первоначально инвестированную сумму (то есть до пре­вышения наличным доходом первоначальных инвестиций). Чем ко­роче период окупаемости, тем инвестиционный проект лучше.

Пример. Определим период окупаемости каждого инвести­ционного проекта из первого примера.

В проекте А для окупаемости первоначальных инвестиций в сум­ме 2 млн. руб. необходимо поступление 0,9 млн. руб. в первый год и (2-0,9) =1,1 млн. руб. (из 1,6 млн. руб.) во второй год. Поэтому пе­риод окупаемости проекта А равен 1 + 1,1/1,6 = 1,7 лет.

В проекте В для окупаемости первоначальных инвестиций в сум­ме 2 млн. руб. необходимо поступление 0,8 млн. руб. в первый год, 1,1 млн. руб. во второй годи 2 - (0,8 + 1,1) = 0,1 млн. руб. (из 0,6 млн. руб.) в третий год. Поэтому период окупаемости проекта В равен 1 + 1 +0,1/0,6 = 2,2 лет.

Так как 1,7 < 2,2, то проект А предпочтительнее.

Задача 22. Определить период окупаемости каждого инвести­ционного проекта в задаче 20.

Недостатки метода окупаемости:

не учитываются потоки денежных средств после завершения срока окупаемости;

не учитывается временная разница поступлений денежных средств (поэтому возможно одобрение инвестиционного проекта с отрицательной чистой приведенной стоимостью).

Учитывая приведенные недостатки, применение метода окупае­мости не обязательно приведет к максимизации рыночной цены обыкновенных акций.

Существует ряд ситуаций, когда целесообразно применение мето­да окупаемости. Например, руководство предприятия в большей сте­пени озабочено решением проблемы ликвидности, а не прибыльно­сти (главное, чтобы инвестиции окупились как можно скорее).

Метод окупаемости также хорош в ситуации, когда инвестиции сопряжены с высокой степенью риска. Например, для отраслей с бы­стрыми технологическими изменениями.

Одна из модификаций метода окупаемости — дисконтирован­ный метод расчета периода окупаемости, когда все потоки денеж­ных средств дисконтированы до их приведенной стоимости, а пе­риод окупаемости определяется на основании дисконтированных потоков.

Окупаемость, рассчитанная по дисконтированным денежным по­токам, достигается в тот момент, когда накопленная приведенная стоимость потоков до этого момента станет равной нулю. Это как раз тот момент времени, когда первоначально инвестированные средст­ва полностью окупаются, а инвестиционный проект начинает при­носить экономическую прибыль. При этом не следует забывать, что дисконтированный срок окупаемости подразумевает неизменность условий реализации инвестиционного проекта.

Дисконтированный метод расчета периода окупаемости также не учитывает все потоки денежных средств после завершения срока окупаемости. Но из-за того, что в дисконтированном методе расчета периода окупаемости полученная величина периода окупаемости больше, чем в методе окупаемости, исключается меньшее количест­во денежных потоков. Поэтому переход от метода окупаемости к дисконтированному методу расчета периода окупаемости — это шаг в правильном направлении.

На практике метод окупаемости очень часто используется для грубой оценки инвестиционных проектов.

Замена оборудования

Особый класс инвестиционных решений - это решения о замене уже имеющихся активов.

Пример. Предприятие рассматривает вопрос о замене обору­дования. Анализ ситуации дал следующую информацию.

 

Показатели	Старое оборудование	Новое оборудование
Стоимость при покупке, руб.
Балансовая стоимость, руб.
Оставшийся срок службы, лет
Производственные затраты, руб./год

 

Ожидается, что как для нового, так и для старого оборудования через 8 лет остаточная стоимость будет равна нулю. Сейчас старое оборудование можно продать за 350000 руб. Альтернативные издерж­ки по инвестициям равны i — 12%. Определим целесообразность за­мены оборудования.

Способ 1. Проведем анализ на основе сопоставления приве­денной стоимости будущих выходящих потоков наличных денежных средств. К таким потокам относятся ежегодные производственные затраты. Первоначальные затраты на приобретение прежнего обору­дования, балансовая стоимость и величина износа за год не являют­ся будущими выходящими потоками наличных денежных средств. Поэтому они не должны включаться в анализ.

Воспользуемся формулой для нахождения современной стоимости для простой ренты постнумерандо

Тогда для старого оборудования приведенная стоимость будущих выходящих потоков наличных денежных средств равна:

375000 × 4,968 + 700000 (покупка нового оборудования) — 350000 (продажа старого оборудования) = 1929824 руб.

Так как 1863000 руб. < 1929824 руб., то следует оставить старое оборудование.

Способ 2. Покупка нового оборудования позволяет ежегодно экономить на затратах 375000 - 318000 = 57000 руб.

Тогда приведенная стоимость экономии на затратах равна 57000 × 4,968 = 283176 руб. Сопоставим эту величину с величиной но­вых инвестиционных затрат: 700000 (покупка нового оборудования) — 350000 (продажа старого оборудования) =350000 руб.

Так как 283176 руб. < 350000 руб., то следует оставить старое оборудование.

Задача 27. Предприятие рассматривает вопрос о замене обору­дования. Анализ ситуации дал следующую информацию.

 

Показатели	Старое оборудование	Новое оборудование
Стоимость при покупке, руб.
Балансовая стоимость, руб.		—
Оставшийся срок службы, лет
Производственные затраты, руб./год

 

Ожидается, что как для нового, так и для старого оборудования через 7 лет остаточная стоимость будет равна нулю. Сейчас старое оборудование можно продать за 410000 руб. Альтернативные издерж­ки по инвестициям равны i = 11%. Определить целесообразность замены оборудования.

Глава 7 Лизинг

Задача 36

Предприятие рассматривает вопрос о приобретении оборудования. Первый вариант — лизинг за 720 тыс. руб. с рассроч­кой платежа в течение четырех лет. Второй вариант — покупка на за­воде-изготовителе за 600 тыс. руб. Ставка налога на прибыль равна К_н = 35%. Предоплата Е_о и остаточная стоимость оборудования Q равны нулю. Можно получить кредит в банке под r =11% годовых. Исполь­зуется равномерное начисление износа. Сравнить эти варианты. Предприятие, использующее значительную часть активов на ос­нове договоров лизинга, обычно обладает меньшими возможностя­ми при выборе дальнейшего варианта финансирования. Ситуация очень похожа на наличие у предприятия значительной долгосрочной задолженности.

Лизинг — это лишь одна из форм финансирования приобретения необходимых активов. Поэтому решение о лизинге должно прини­маться после того, как проведены расчеты экономических показате­лей денежных потоков и стоимости предприятия.

Глава 10 Облигации

10.1 Основные определения

Двумя основными формами корпоративного капитала являются кредит и обыкновенные акции. В этой главе мы рассмотрим оценку стоимости облигаций — основного типа долгосрочных кредитов.

Облигация — это долговое обязательство, выпускаемое коммерче­ской компанией или государством, в соответствии с которым эми­тент (то есть заемщик, выпустивший облигацию) гарантирует креди­тору выплату определенной суммы в фиксированный момент времени в будущем и периодическую выплату назначенных процен­тов (по фиксированной или плавающей процентной ставке).

Номинальная (нарицательная) стоимость облигации — это величи­на денежной суммы, указанная на облигации, которую эмитент берет взаймы и обещает выплатить по истечении определенного срока (срока погашения).

Дата погашения — это день, когда должна быть выплачена номи­нальная стоимость облигации. Многие облигации содержат условие, по которому эмитент имеет право выкупа облигации до истечения срока погашения. Такие облигации называются отзывными. Эмитент облигации обязан периодически (обычно раз в год или полгода) вы­плачивать определенные проценты от номинальной стоимости обли­гации.

Купонная процентная ставка — это отношение суммы выплачива­емых процентов к номинальной стоимости облигации. Она опреде­ляет первоначальную рыночную стоимость облигации: чем выше ку­понная процентная ставка, тем выше рыночная стоимость облигации. В момент выпуска облигации купонная процентная став­ка полагается равной рыночной процентной ставке.

В течение месяца с момента выпуска облигации называются обли­гациями нового выпуска. Если облигация продается на вторичном рынке более месяца, то она называется обращающейся облигацией.

 

Литература

1. Бирман Г., Шмидт С. Капиталовложения: Экономический анализ инвес­тиционных проектов. — М.: ЮНИТИ, 2003.

2. Бланк И. А. Управление финансовыми рисками. — К.: Ника-Центр, 2005.

3. Бороздин Л. Ю. Ценные бумаги и фондовый рынок. — М.: Вейл, 1994.

4. Ван Хорн Дж. К. Основы управления финансами. — М.: Финансы и ста­тистика, 2000.

5. Друри К. Управленческий учет для бизнес-решений. — М.: ЮНИТИ, 2003.

6. Ковалев В. В. Введение в финансовый менеджмент. — М.: Финансы и ста­тистика, 1999.

7. Миддлтон Д. Бухгалтерский учет и принятие финансовых решений. — р ЮНИТИ, 1997.

8. Норткотт Д. Принятие инвестиционных решений. — М.: ЮНИТИ, 1997.

9. Пейли П. Успешный бизнес-план. От стратегических целей к плану действий на один год. — М.: Эксмо, 2007.

10. Просветов Г. И. Анализ хозяйственной деятельности предприятия: Зада­чи и решения. 4-е изд. — М.: Издательство РДЛ, 2007.

11. Просветов Г. И. Математика в экономике: Задачи и решения. 2-е изд. — М.: Издательство РДЛ, 2005.

12. Просветов Г. И. Математические методы в экономике. 3-е изд. — М.: Из­дательство РДЛ, 2007.

13. Просветов Г. И. Математические модели в экономике. 2-е изд. — М.: Из­дательство РДЛ, 2006.

14. Просветов Г. И. Эконометрика: Задачи и решения. 4-е изд. — М.: Изда­тельство РДЛ, 2007.

15. Савицкая Г. В. Экономический анализ. — Мн.: Новое знание, 2004.

16. Скеллон Н. Бизнес COMBAT. — М.: Эксмо, 2004.

17. Тиффани П., Питерсон С. Бизнес-планы для «чайников». — М.: Вильяме, 2007.

18. Хелферт Э. Техника финансового анализа. — СПб.: Питер, 2003. Шарп У., Александер Г., БейяиДж. Инвестиции. — М.: ИНФРА-М, 2001. Шмидт Р. А., Райт X. Финансовые аспекты маркетинга. — М.: ЮНИТИ, 2000.

Содержание

Введение. 3

Глава 1 Стоимость денег во времени. 5

1.1 Простые ставки ссудных процентов. 5

1.2 Сложные ставки ссудных процентов. 10

1.3 Математическое дисконтирование. 12

Глава 2 Модели финансовых потоков. 18

2.1 Основные понятия. 18

2.2 Взаимосвязь между шестью функциями сложного процента. 25

Дополнительные функции. 26

2.3 Различные схемы погашения кредита. 31

Глава 3 Амортизация. 36

3.1 Методы начисления износа. 36

3.2 Сравнение методов начисление амортизации. 40

Глава 4 Методы оценки инвестиций в условиях определенности. 44

4.1 Общие принципы принятия инвестиционного решения. 44

4.2 Сравнение методов чистой приведенной стоимости и внутренней нормы доходности. 51

4.3. Учетный коэффициент окупаемости инвестиций. 55

Глава 5 Налогообложение и инвестиционные решения. 59

5.1 Влияние налогов на величину чистой приведенной стоимости инвестиционного проекта. 59

5.2 Прибыли или убытки от продажи имущества. 62

5.3 Сравнение инвестиционных проектов с разными сроками реализации 64

5.4. Замена оборудования. 66

Глава 6 Учет инфляционного обесценения денег. 69

6.1 Уровень (темп) инфляции. Индекс инфляции. 69

6.2 Ставка, учитывающая инфляцию, для случая простых процентов. Формула Фишера. 70

6.3 Ставка, учитывающая инфляцию, для случая сложных процентов. 73

6.4. Оценка чистой приведенной стоимости инвестиционного проекта в условиях инфляции. 75

Глава 7 Лизинг. 78

7.1 Преимущества и недостатки лизинга. 78

7.2 Сравнительный анализ эффективности лизинга и банковского кредитования покупки основных средств. 79

Глава 8 Зарубежные инвестиции. 84

8.1 Требуемая доходность в иностранной валюте. 84

8.2 Чистая приведенная стоимость зарубежных инвестиций. 85

Глава 9 Применение математического ожидания и стандартного отклонения для оценки риска. 87

Глава 10 Облигации. 90

10.1 Основные определения. 90

10.2 основные методы оценки стоимости облигаций. 91

10.3 Доходность облигации при погашении в конце срока. 94

10.4 Доходность отзывных облигаций. 97

Задачи для самостоятельной подготовки. 100

Литература. 114

 

[1] Внутренняя норма отдачи (IRR) – это норма дисконтирования, при которой настоящая стоимость всех будущих денежных потоков равна сумме начальных инвестиций.

Е. А. Боркова

СТРАТЕГИЧЕСКОЕ ПЛАНИРОВАНИЕ –

Задачи и решения

практикум

 

 

Специальность 080103 – Национальная экономика

Направление 080100 - Экономика

 

 

Санкт-Петербург

 

УДК 005.511

ББК 65.290-2

П 82

Утверждено

редакционно-издательским советом СПбГИЭУ

Рецензенты:

 

А.И. Стешин, д.э.н., профессор, зав. кафедрой «Менеджмент организации» БГТУ «Военмех» им. Д.Ф. Устинова.

 

З.А. Сизенова, к.э.н. доцент, Санкт-Петербургского государственного университета экономики и финансов.

 

 

Боркова Е. А.

Стратегическое планирование - Задачи и решения: практикум. СПб.: СПбГИЭУ, 2009. – 116 с.

В учебно-практическом пособии раскрываются основы системного подхода к процессу бизнес-планирования как многофункциональному инструменту управления.

Рассматриваются методы, варианты, общие и частные случаи бизнес-планирования. Приведены экономические, финансово-кредитные, организационно-управленческие задачи, встречающиеся в бизнес-планировании.

Предназначено для студентов, обучающихся по специальности 080103 – Национальная экономика, по направлению 080100 – Экономика.

 

 

© СПбГИЭУ, 2009

Введение

Логика развития и динамика современного рынка ясно свидетельствуют – ни один успешный предприниматель уже не может обойтись без плана развития своего бизнеса. Причем этот план, просто обязан быть составлен на высоком профессиональном уровне. Без детального бизнес-планирования не обойтись не только на этапе создания своего дела, но и на стадиях продвижения товара или услуги на рынок, расширения бизнеса, при выходе на новые рынки, а также в случае реорганизации компаний и производств, осуществлении инвестиционных проектов.

Прежде чем начать какое-либо дело, человек должен тщательно продумать, что именно, к какому сроку, какими способами и с помощью каких средств он должен сделать. В противном случае его намерения могут оказаться невыполненными. Бизнес-планирование позволяет не только обосновать необходимость разработки того или иного инвестиционного проекта, но и возможность его реализации в действующих рыночных условиях.

Цель этого учебно-практического пособия – изложить студентам основные, повсеместно используемые приемы и методы бизнес-планирования, а также объяснить, как и когда следует применять эти приемы и методы, чтобы получить осмысленные решения и ответы.

Весь материал разбит на главы, а главы на параграфы. Каждый параграф – это отдельная тема. В начале параграфа приводится необходимый минимум теоретических сведений, затем подробно разбираются модельные примеры. Показано, как с помощью встроенных функций и надстройки «Пакета анализа» пакета Excel можно избежать долгих и утомительных вычислений. После каждого примера приводится задача для самостоятельного решения.

Структура практикума в соответствии с поставленными задачами включает следующие темы:

1. Стоимость денег во времени.

2. Модели финансовых потоков.

3. Амортизация

4. Методы оценки инвестиций в условиях определенности.

5. Налогообложение и инвестиционные решения.

6. Учет инфляционного обесценения денег

7. Лизинг

8. Зарубежные инвестиции

9. Применение математического ожидания и стандартного отклонения для оценки риска

10. Облигации

Глава 1 Стоимость денег во времени