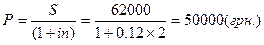Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Врахування інфляції в ставці простих відсотків.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При обчисленні вартісних величин необхідно враховувати вплив інфляції. При обчисленні простих відсотків зручно враховувати вплив інфляції у відсотковій ставці. Позначимо рівень інфляції через ψ, який визначається як коефіцієнт приросту: ψ = Іінф – 1, де Іінф – індекс інфляції в коефіцієнтах. Тоді втрати від інфляції становитимуть: ∆Sψ = S x ψ = Сума захищена від інфляції буде включати кінцеву суму боргу та відшкодування можливих втрат від інфляції:
З іншого боку, можна обчислити кінцеву суму боргу захищену від інфляції із застосуванням відсоткової ставки, що враховує інфляційний вплив:
де Очевидно, що рівність лівих частин формул (1) та (2), означає рівність правих частин. Тоді:
Після скорочень та розкриття дужок розрахуємо:
Якщо відсоткова ставка невелика, інфляція низька, строк позики малий, тоді останнім доданком у формулі можна нехтувати: Приклад 6. Позику розміром 500 тис. грн. видано 13.02.2001, погашено 18.10.2001, проста декурсивна ставка відсотків 10%. Індекс інфляції склав 115%. Визначити за формулою розрахунку точних відсотків просту ставку відсотків, що враховуватиме інфляцію, а також суму платежу з врахуванням інфляції. Розв’язання: За таблицею порядкових номерів днів у році: 13.02.2001 – день № 44; 18.10.2001 – день №. 291. Точна кількість днів позики: q точне = № дати погашення - № дати надання = 291 – 44 = 247 (днів). Рівень інфляції в коефіцієнтах: ψ = Іінф – 1 = 1.15 – 1 = 0.15 Проста ставка відсотків, що враховує інфляцію:
Сума платежу з врахуванням інфляції:
Відповідь: проста ставка відсотків, що враховуватиме інфляцію дорівнює 26%, сума платежу з врахуванням інфляції дорівнює 587972.60 грн.
Обчислення складних відсотків. Якщо відсотки кожен раз нараховуються від нарощеної суми, тобто від суми збільшеної за рахунок приєднання до неї відсотків, тоді нараховані відсотки – складні. Нарахування відсотків з приєднанням їх до основної суми боргу називають капіталізацією суми боргу або нарахуванням відсотків від змінної бази нарахування. Обчислимо складні відсотки за декурсивною ставкою (і). Нараховані відсотки кожен раз будуть мати іншу величину:
Нарощена сума буде розраховуватись за наступною формулою:
Загальна формула розрахунку нарощеної суми (вартості) за складними відсотками має вигляд:
Вираз За обліковою ставкою відсотків (d) нарахування складних відсотків проводиться за формулою:
де Складні відсотки мають широке застосування у фінансових обчисленнях зокрема та економічних розрахунках загалом. Їх формули розрахунку використовують як для довгострокових, так і для короткострокових розрахунків. Приклад 7. Нарощена сума склала 6 тис. грн., декурсивна відсоткова ставка – 4% річних, строк зберігання грошей – 20 місяців. Визначити початкову суму грошей за простими та складними відсотками. Розв’язання: 1.Початкова сума грошей за простими відсотками дорівнює:
2. Початкова сума грошей за складними відсотками дорівнює:
Відповідь: початкова сума боргу за простими відсотками становить 3.3 тис. грн., за складними відсотками – 2.7 тис. грн.
Врахування інфляції в розрахунках складних відсотків. При застосуванні схем складних відсотків інфляцію враховують за допомогою індексу купівельної спроможності грошей (Ікс). Цей індекс зворотній до індексу інфляції (Іінф). Реальна кінцева сума боргу за схемою складних відсотків буде розраховуватись за формулою:
Ікс можна виразити через рівень інфляції ψ: Приклад 8. Якою буде реальна купівельна спроможність суми 100 тис. грн. через три роки, якщо нараховуються 16% в рік за ставкою складних відсотків, а прогнозований рівень інфляції 15% щороку? Розв’язання:
Відповідь: Реальна купівельна спроможність 100 тис. грн. через три роки буде дорівнювати 102631,45 грн.
Дисконтування. Нарощення відбувається з плином часу. Якщо розглянути процес кількісної зміни величини у зворотному порядку, побачимо зменшення величини грошей. Такий метод розрахунку називають дисконтуванням. Іншими словами, дисконтування – це визначення величини вартісного показника на заданий момент часу (інколи кажуть: зведення вартісного показника до заданого моменту часу). Різницю між значеннями вартісного показника за різні моменти часу називають дисконтом. Математичне дисконтування. Для математичного дисконтування використовують декурсивну ставку відсотків (і). Поточну суму боргу (Р) можна обчислити за наступними формулами: 1) просте дисконтування:
де 2) складне дисконтування:
де Приклад 9. Якої величини капітал, розміщений під 12% простих річних, принесе 62 тис. грн. через два роки? Якої величини буде дисконт? Розв’язання:
D = S – P = 62000 – 50000 = 12000 (грн.) Відповідь: Потрібен капітал 50 тис. грн., дисконт складе 12 тис. грн.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.253.73 (0.009 с.) |

 .
.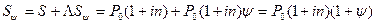 (1)
(1) (2),
(2),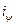 - ставка, що враховує інфляцію.
- ставка, що враховує інфляцію. .
. .
.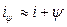 .[4]
.[4] (або 26%)
(або 26%)
 ;
;  ;... і т.п.
;... і т.п. ;
;  ;... і т.п.
;... і т.п.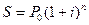 .
. називають множником нарощення складних відсотків за декурсивною ставкою. Значення цього множника часто для зручності наводять в таблицях складних відсотків. Точність обчислення в практичних розрахунках визначається граничним ступенем заокруглення нарощеної суми. [5]
називають множником нарощення складних відсотків за декурсивною ставкою. Значення цього множника часто для зручності наводять в таблицях складних відсотків. Точність обчислення в практичних розрахунках визначається граничним ступенем заокруглення нарощеної суми. [5] ,
,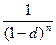 - множник нарощення складних відсотків за обліковою ставкою.
- множник нарощення складних відсотків за обліковою ставкою. тис. грн.
тис. грн.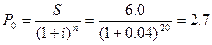 тис. грн.
тис. грн.
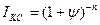 , тоді реальна кінцева сума боргу за схемою складних відсотків буде розраховуватись так:
, тоді реальна кінцева сума боргу за схемою складних відсотків буде розраховуватись так: 

 ,
, - простий дисконтний множник (величина обернена до множника нарощення простих відсотків);
- простий дисконтний множник (величина обернена до множника нарощення простих відсотків); ,
, - складний дисконтний множник (величина обернена до множника нарощення складних відсотків).
- складний дисконтний множник (величина обернена до множника нарощення складних відсотків).