
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фінансові потоки, їх значення та характеристика.Содержание книги
Поиск на нашем сайте В сучасному фінансовому аналізі часто виникає потреба в оцінюванні та зміні не окремого платежу, а деякої послідовності платежів. З послідовними платежами зустрічаються в інвестиційних процесах, пенсійних платежах, нарахуванні абонентської плати та в багатьох інших випадках. Множину розподілених в часі платежів називають фінансовим потоком або потоком платежів. Загалом, кожен навіть окремий платіж теоретично можна представити як потік платежів, що складається з одного члена потоку. Члени потоку платежів можуть бути як додатними величинами, так і від’ємними. [3] Фінансовою рентою (або ануїтетом) називають фінансовий потік платежів, величини всіх членів якого додатні, часові інтервали між двома послідовними платежами постійні, незалежно від походження та призначення цих платежів. Фінансовими рентами є, наприклад, виплати споживчого кредиту, пенсійні платежі, абонентська плата за телефон, створення амортизаційного фонду та ін. Введемо позначення параметрів ренти: · член ренти (R) – величина кожного окремого платежу; · період ренти (p) – часовий проміжок між двома послідовними платежами; · строк ренти (n) – час від початку ренти до кінця останнього періоду; · відсоткова ставка (i, d) – ставка відсотків, яка використовується для нарощення або дисконтування членів ренти. Ренти розрізняють за наступними ознаками [4]: 1) за тривалістю періоду ренти бувають: - річні (p=1); - p-термінові (p≠1). 2) за частотою платежів: - дискретні (періодична сплата); - неперервні (дуже часто сплачуються, практично безперервно). 3) за частотою нарахувань відсотків: - нарахування один раз на рік; - нарахування m раз на рік. 4) за величиною членів: - постійні (з рівними членами); - змінювані (з різними членами). 5) за числом членів: - обмежені (скінчене число членів); - необмежені, „вічні” (нескінчене число членів). 6) за ймовірністю здійснення платежів: - безумовні правильні (платежі здійснюються обов’язково); - умовні (число членів наперед невідоме). 7) за моментами виплат: - звичайні, постнумерандо (платежі здійснюють наприкінці періоду); - авансові, преднумерандо (платежі вносять на початку кожного періоду). 8) за відповідністю початку ренти і певного фіксованого моменту часу (початок дії контракту, час оцінки ренти): - термінові (обидва моменти збігаються); - відстрочені, відкладені (початок строку ренти запізнюється відносно вказаного моменту). Нарощена сума ренти являє собою суму членів ренти, нарощених за весь період ренти. Розглянемо розрахунок нарощеної суми обмеженої річної ренти постнумерандо. Розрахунок проводиться на кінець строку ренти. В кінці строку ренти різні платежі будуть мати різну величину, оскільки, платежі внесені в різний час, і до кожного платежу приєднана різна кількість відсоткових грошей: Величина останнього платежу складатиме - R; Величина передостаннього платежу складатиме - R(1+і)1 ................................................................................................................ Величина третього платежу складатиме - R(1+і)n-3 Величина другого платежу складатиме - R(1+і)n-2 Величина першого платежу складатиме - R(1+і)n-1 В кінці строку ренти сума всіх нарощених членів ренти (S) складатиме: S = R + R(1+і)1 + … + R(1+і)n-3 + R(1+і)n-3 + R(1+і)n-2 + R(1+і)n-1 Ця послідовність являє собою геометричну прогресію з першим членом R і знаменником прогресії (1+і). Підставимо параметри прогресії у формулу суми членів скінченої геометричної прогресії та отримаємо формулу нарощеної суми обмеженої річної ренти постнумерандо:
де Приклад 14. Створюється фонд, куди вносять внески протягом 10 років у розмірі 1 тис. грн. На зібрані кошти нараховується 12% складних річних. Якої величини буде фонд через 10 років? Розв’язання:
Відповідь: через 10 років величина фонду становитиме 17548.74 грн.
Якою буде сума членів ренти в різні періоди часу в межах строку ренти? Для відповіді на таке питання потрібно спочатку привести (дисконтувати) вартість всіх членів ренти до потрібного моменту часу, а потім їх додати. В результаті отримаємо поточну вартість ренти. [6] Поточна вартість ренти – це сума всіх дисконтованих членів потоку платежів на певний момент часу. Такі розрахунки проводяться при погашенні боргів, визначенні ефективності різних фінансових операцій, в страхових розрахунках і т.п. Оцінимо вартість обмеженої ренти в момент початку ренти. Дисконтова ні платежі цієї ренти утворять ряд:
Цей ряд являє собою скінчену геометричну прогресію з першим членом R і знаменником прогресії Сума членів цієї прогресії розраховується за формулою суми членів скінченої геометричної прогресії. Таким чином поточна вартість ренти (А) на початку строку ренти обчислюється:
де Приклад 15. Вкладник протягом 5 років хоче отримувати щорічний дохід 12 тис. грн. Депозитна ставка банку – 8%. Визначити поточну вартість цієї ренти. Розв’язання:
Відповідь: поточна оцінка майбутніх щорічних платежів розміром 12 тис. грн. складає 47912.52 грн.
Для вічної ренти, де кількість платежів необмежена, можемо обчислити поточну вартість ренти за наступною формулою:
Приклад 16. Якою є поточна вартість акції з щорічним дивідендом 20 грн., якщо дисконтна відсоткова ставка для подібних акцій складає 5%? Розв’язання:
Відповідь: поточна вартість такої акції 400 грн.
Питання для самоконтролю. 1. Які Ви знаєте основні завдання вищих фінансових обчислень? 2. Чому відбувається нарощення (зростання) величини вартісного показника з плином часу? 3. Які Ви знаєте види відсотків і відсоткових ставок? У чому полягає різниця між ними? 4. Як відбувається нарощення за схемою простих відсотків і за схемою складних відсотків? 5. Як відбувається нарощення за обліковою і декурсивною ставками? 6. Як враховується вплив інфляції в схемах простих і складних відсотків? 7. Як розрахувати кінцеву суму боргу за змінюваною ставкою простих відсотків? 8. Що таке дисконтування і дисконт? Які Ви знаєте різновиди дисконтування? 9. Поясніть принцип еквівалентності і покажіть, як розраховуються взаємноеквівалентні проста і складна, декурсивна і облікова ставки відсотків. 10. У чому різниця між номінальною ставкою і ставкою ефективності? Як відбувається капіталізація суми боргу за цими ставками? 11. Що входить в поняття фінансового потоку і фінансової ренти? 12. Які види фінансових рент Ви знаєте? 13. Як розрахувати нарощену суму ренти? 14. Як визначити поточну вартість ренти? 15. Що входить в поняття вічної ренти і як обчислити її поточну вартість? Тестові завдання. 1. Відсотки у фінансових розрахунках це: 1) плата за користування позиченими грошима, капіталом; 2) частка плати за користування позиченими грошима чи капіталом у кінцевій сумі боргу; 3) різниця між позиченою сумою та платою за користування позиченими грошима; 4) відношення позиченої суми до плати за користування нею.
2. Відсоткова ставка у фінансових розрахунках це: 1) плата за користування позиченими грошима, капіталом; 2) пропорція між позиченою сумою та кінцевою сумою боргу; 3) відношення величини позички (суми боргу) до суми відсоткових грошей, виплачених за певний період часу (рік, місяць). 4) відношення суми відсоткових грошей, виплачених за певний період часу (рік, місяць) до величини позички (суми боргу).
3. Відсотки вимірюються у: 1) %; 2) коефіцієнтах; 3) ‰; 4) грошових одиницях.
4. Відсоткова ставка вимірюється у: 1. %; 2. коефіцієнтах; 3. ‰; 4. грошових одиницях.
5. При нарахуванні за обліковою ставкою сума, яка видається позичальнику: 1) менша від кінцевої суми боргу на величину відсоткових грошей; 2) дорівнює величині відсоткових грошей; 3) більша від кінцевої суми боргу на величину відсоткових грошей; 4) дорівнює кінцевій сумі боргу.
6. Якщо кожне нарахування відсотків проводиться від однієї суми (постійна база нарахування), тоді це: 1) прості відсотки; 2) дисконт; 3) рента; 4) складні відсотки.
7. Якщо кожне нарахування відсотків проводиться від суми, що нарощена додаванням відсотків за попередній період (змінювана база нарахування), тоді це: 1) прості відсотки; 2) складні відсотки; 3) рента; 4) дисконт.
8. Які види простих відсотків більш вигідні кредитору: 1) звичайні; 2) комерційні; 3) точні; 4) жоден з перелічених.
9. Які види простих відсотків більш вигідні позичальнику: 1) звичайні; 2) комерційні; 3) точні; 4) жоден з перелічених
10. Якщо позначити через і - просту ставку відсотків, через іτ – просту ставку відсотків, яка враховує інфляцію; через τ - річний рівень інфляції в коефіцієнтах; через n – роки; тоді як виразити залежність іτ від і, τ, n: 1) іτ = i x τ x n 2) іτ = i + τ + τ x n 3) іτ = i + τ – τ x n 4) іτ = i + τ + i x τ x n
11. Дисконт це: 1) кінцева сума боргу за обліковою ставкою; 2) різниця між значеннями вартісного показника за різні моменти часу; 3) кінцева сума боргу за вирахуванням відсотків; 4) поточна сума боргу.
12. Математичне дисконтування проводиться за: 1) обліковою ставкою; 2) правилами нарахування ренти; 3) методами врахування інфляції у фінансових обчисленнях; 4) декурсивною ставкою відсотків.
13. Банківське дисконтування проводиться за: 1) обліковою ставкою; 2) правилами нарахування ренти; 3) методами врахування інфляції у фінансових обчисленнях; 4) декурсивною ставкою відсотків.
14. Якщо S – кінцева сума боргу; Ро – початкова сума боргу; d – облікова ставка; n – кількість періодів нарахування відсотків, тоді як відбувається нарощення за простою обліковою ставкою: 1) S = P/(1- d x n); 2) S = P x (1- d x n); 3) S = P x (1 + d x n); 4) S = P x (1- d + n).
15. Якщо і – ставка відсотків; d – облікова ставка; P – поточна сума боргу; n – кількість періодів нарахування відсотків, тоді проста декурсивна ставка відсотків, яка еквівалентна простій обліковій ставці, розраховується: 1) і = d /(1- d x n); 2) і = d x (1- d x n); 3) S = P /(1- d x n); 4) і = d x (1 + d x n).
16. Якщо і – ставка відсотків; d – облікова ставка; n – кількість періодів нарахування відсотків, тоді проста облікова ставка, яка еквівалентна простій декурсивній ставці відсотків розраховується: 1) d = і / (1- і x n); 2) 2) d = і x (1+ і x n); 3) S = P /(1- d x n); 4) d = і x (1 - і x n).
17. Еквівалентними вважаються платежі, які за умови зведення за даною відсотковою ставкою до одного моменту часу є: 1) нерівними; 2) рівними; 3) погашаються в один момент часу; 4) пропорційними.
18. Капіталізація відсотків це: 1) процес нарахування складних відсотків і приєднання їх до бази нарахування; 2) формування консолідованого платежу; 3) процес нарахування простих відсотків і формування кінцевої суми боргу; 4) визначення поточної суми боргу.
19. Що вимірюють ефективні ставки відсотків: 1) реальний відносний дохід, який вимірюють в цілому за рік; 2) реальний абсолютний дохід, який отримують в цілому за рік; 3) дохід від вкладених коштів, який визначається за річною ставкою відсотка; 4) нічого з викладеного.
20. Фінансовою рентою (ануїтетом) називається: 1) нарахування складних відсотків; 2) фінансовий потік платежів, величини всіх членів якого додатні, часові інтервали між двома послідовними платежами постійні, незалежно від походження та призначення цих платежів; 3) плата за кредит; 4) об’єднання кількох боргових зобов’язань (платежів) в одне боргове зобов’язання.
21. Виберіть, які фінансові платежі можна вважати фінансовою рентою: 1) платежі, що створюють пенсійний фонд; 2) сплата дивідендів від акцій; 3) погашення векселя; 4) виплата споживчого кредиту.
Практичні завдання
Завдання 1. Позичку у 200 тис. грн. надано під 20% річних простих на 1 рік. Визначити суму відсотків та суму кінцевого платежу. Якою буде сума кінцевого платежу, якщо через 4 місяці ставку збільшили до 25%, через 6 місяців - до 30%, а через 9 місяців - до 45%?
Завдання 2. 1 лютого 2004 р. надана позичка у 100 тис. грн. до 25.05.2004 під 10% річних. Визначити яку суму відсотків потрібно заплатити у день погашення за умови нарахування відсотків: а) звичайних; б) комерційних; в) точних. Обчисліть зміну кінцевої суми боргу в кожному випадку.
Завдання 3. Надано 3-річний споживчий кредит на суму 360 тис. грн. під 45% простих річних за умови щомісячного погашення. Визначити суму щомісячного платежу та кінцеву суму боргу.
Завдання 4. Позичку у 80 тис. грн. надано на строк від 20.03 до 17.09 під 8% річних. Визначити ставку простих відсотків та суму платежу з врахуванням інфляції, якщо річний темп росту інфляції 110,1%.
Завдання 5. Річні кредити видано під річні облікові ставки:
Визначити: 1) суму виплачену клієнту; 2) величину дисконту.
Завдання 6. Визначити кінцеві суми боргу за умови нарахування складних відсоткових ставок:
Завдання 7. На внески банк нараховує 20% річних. Інфляція складає 10% в рік. Процентні суми нараховуються один раз у рік за формулою складних відсотків. Яка реальна сума буде нагромаджена за 8 років, якщо розмір внеску дорівнює 120 тис. грн.? Завдання 8. На внесену щорічно ренту (400 тис. грн.) банк за ставкою 20% щорічно нараховує складні відсотки. Визначить суму коштів через 10 років. Завдання 9. Визначить сучасну величину ренти, нагромаджену в результаті щорічних внесків у розмірі 5 тис. грн. протягом 4 років. Процентна ставка — 25%. Завдання 10. Обчислити суму, яку потрібно внести на рахунок в банку, щоби виплачувати протягом 4 років наприкінці року додаткову пенсію в сумі 1000 грн. Банк нараховує відсотки в кінці року в розмірі 8% складних річних. Завдання 11. Вексель зі строком погашення 2 міс. і номіналом 900 тис. грн., по якому щомісячно нараховується 4% простих, куплений банком за місяць до строку за ставкою 36,4% річних. Якою була поточна вартість векселя? Завдання 12. Нарощена сума склала 6 млн. грн., відсоткова ставка – 16% річних, строк зберігання грошей – 4 роки. Визначити первинну суму грошей за простими та складними відсотками. Завдання 13. Річний кредит розміром 100 тис. грн. видано під річну облікову ставку 15%. Визначити суму, одержану клієнтом у розпорядження.
Завдання 14. Якою буде кінцева сума боргу та відсотки, якщо в угоді передбачено за перші два роки нарахування 20% річних, а в наступні два роки ставка відсотків збільшується щорічно на 5%? Початкова сума боргу становить 100 тис. грн. Завдання 15. Позичку величиною 200 тис. грн. надано 23.02.2000 р., погашено 10.08.2000 р. Обчислити звичайні, комерційні та точні відсотки. Завдання 16. Надано споживчий кредит величиною 2000 грн. під 25% річних. Якою буде сума разового погашувального платежу, якщо планується сплачувати борг протягом одного року щоквартально. Завдання 17. Позичено 20 тис. грн. під 24% річних простих на 6 місяців. Відсотки нараховуються щомісяця. Розрахуйте: 1) кінцеву суму боргу; 2) суму відсотків; 3) ставку ефективності; 4) ставку простих відсотків, що враховує інфляцію, при щомісячному індексі інфляції 100,05%. Завдання 18. Проведіть операцію обліку векселя номіналом 1000 грн. 01.08.2002, якщо оплата векселя 01.11.2002, облікова ставка становить 20%. Завдання 19. Визначити, яку облікову ставку застосував банк, коли заплатив 1500 грн. за вексель номіналом 1600 грн. Термін платежу за векселем настає через 3 місяці. Завдання 20. Кредит величиною 100 тис. грн. надано на рік під 24% річних складних. Якою буде ставка ефективності, якщо нарахування відсотків відбувається: а) щомісяця; б) щокварталу; в) щопівроку? Завдання 21. Кредит величиною 100 тис. грн. надано на рік під 36% річних складних. Якою буде еквівалентна ставка простих відсотків, якщо нарахування відсотків відбувається: а) щомісяця; б) щокварталу; в) що півроку? Завдання 22. Яку суму отримав у розпорядження боржник, якщо він сплатив кредитору 24000 грн. за 2 роки під ставку 20% річних простих? Завдання 23. Якою буде сума дисконту при продажу фінансового інструменту на суму 5000 грн., якщо строк його погашення становить 2 роки, а покупець застосовує складну річну облікову ставку 20%?
Рекомендована література:
1. Ковалев В.В., Уланов В.А. Курс фінансовых вычислений. – М.: Финансы и статистика, 2001. – 328 с. 2. Кочович Е. Финансовая математика: Теория и практика финасово-банковских расчетов. – М.: Финансы и статистика, 1995. 3. Кутузов В.Б. Основы финансовой и страховой математики: Методы расчета кредитных, инвестиционных, пенсионных и страховых схем. – М.: Дело, 1998.- 304 с. 4. Лапішко М.Л. Основи фінансово-статистичного аналізу економічних процесів: Підручник. – Львів: Світ, 1995. 5. Машина Н.І. Вищі фінансові обчислення: Навчальний посібник. – К.: Центр навчальної літератури, 2003. – 208 с. 6. Статистика финансов: Учебник / Под ред. проф. В.М. Салина. - М.: Финансы и статистика, 2000. - 816с. 7. Уланов В.А. Сборник задач по курсу финансовых вичислений / Под ред. Проф.. В.В.Ковалева. – М.: Финансы и статистика, 2000. – 400 с. 8. Четыркин Е.М. Финансовая математика: Учеб. - М.: Дело, 2001. – 400 с. 9. Шустіков А.А.Фінансова статистика:Навч.посібник.-К.:КНЕУ,2002.-
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 ,
, - коефіцієнт нарощення ренти, значення якого часто подають в таблицях.
- коефіцієнт нарощення ренти, значення якого часто подають в таблицях.
 ;
;  ;
;  ;...;
;...; 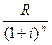 .
. . Знаменник прогресії можна більш компактно представити у вигляді
. Знаменник прогресії можна більш компактно представити у вигляді  .
. ,
, - коефіцієнт зведення ренти.
- коефіцієнт зведення ренти.
 .
.



