
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отношение эквивалентности. Связь отношения эквивалентности с разбиением множества на классы. Отношение порядка. Строгий и нестрогий порядок. Линейный и частный порядок. Упорядоченные множества.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Эквивалентность – это равнозначность (или равноценность) в каком-нибудь отношении. Отношение Пусть Например, разбиение состоит из подмножеств множества Пустое отношение (на непустом множестве!) не является эквивалентностью. Мы подошли к эквивалентности через понятие взаимозаменимости. Но что значит, что два объекта Например, пусть считаем одинаковыми автомобили, выпущенные в одной и той же серии одним и тем же заводом. Тогда, разобрав один экземпляр «Волги», в принципе можем составить комплект рабочих чертежей, который годится для выпуска однотипных «Волг». Однако, изучив один экземпляр «Волги», не можем угадать окраску кузова или характер вмятин на бампере у других односерийных экземпляров. Когда мы выбираем из комплекта одну шахматную фигуру, то мы знаем, куда ее можно поставить в начальной позиции и как ходят, все взаимозаменяемые с ней, т.е. одноименные и одноцветные, фигуры. Пусть теперь задано разбиение
Легко видеть, что эквивалентность Ясно, что любое отношение эквивалентности может быть таким образом определено с помощью отношения «быть эталоном» и, наоборот, любое отношение «быть эталоном» определяет некоторую эквивалентность. Пусть Иначе говоря, Рассмотрим в качестве
|
|||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 750; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.164.202 (0.011 с.) |

 на множестве
на множестве 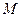 называется эквивалентностью (или отношением эквивалентности), если существует разбиение
называется эквивалентностью (или отношением эквивалентности), если существует разбиение  множества
множества  выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда  и
и  принадлежат некоторому общему классу
принадлежат некоторому общему классу  данного разбиения.
данного разбиения. . Наконец, если разбиение множества
. Наконец, если разбиение множества  . Этот элемент мы будем называть эталоном для всякого элемента
. Этот элемент мы будем называть эталоном для всякого элемента  . Так определенное отношение
. Так определенное отношение  , соответствующая исходному разбиению, может быть определена так:
, соответствующая исходному разбиению, может быть определена так:  , если
, если  имеют общий эталон:
имеют общий эталон:  .
. – такое отношение «быть эталоном», что
– такое отношение «быть эталоном», что  и
и  . Поскольку
. Поскольку  , это означает, что
, это означает, что  . Иначе говоря, эквивалентность можно алгебраически выразить через более простое отношение «быть эталоном». Отношение
. Иначе говоря, эквивалентность можно алгебраически выразить через более простое отношение «быть эталоном». Отношение  элементов можно задать графом, имеющим ровно
элементов можно задать графом, имеющим ровно  стрелок, где
стрелок, где  – число классов эквивалентности: каждый элемент соединяется со своим единственным эталоном. Граф, изображающий отношение эквивалентности, состоит из
– число классов эквивалентности: каждый элемент соединяется со своим единственным эталоном. Граф, изображающий отношение эквивалентности, состоит из  , вершин
, вершин 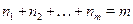 . Таким образом, общее число ребер в этом графе равно
. Таким образом, общее число ребер в этом графе равно  .
. четных чисел и множество
четных чисел и множество  нечетных чисел. Соответствующее отношение эквивалентности на множестве целых чисел обозначается так:
нечетных чисел. Соответствующее отношение эквивалентности на множестве целых чисел обозначается так: 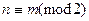 и читается:
и читается:  подмножеств
подмножеств  , где
, где  , мы придем к отношению эквивалентности:
, мы придем к отношению эквивалентности: 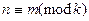 , которое выполняется, если
, которое выполняется, если 


