
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретико-множественный смысл суммы целых неотрицательных чисел. Законы сложения (с доказательством).Содержание книги
Поиск на нашем сайте
Сложение целых неотрицательных чисел связано с объединением конечных непересекающихся множеств. Если a = n(A), b = n(B) иA Докажем сначала, что если a и b - натуральные числа, то существует взаимно однозначное отображение отрезка натурального ряда N Пусть a = n(A), b = n(B). Тогда существует взаимно однозначные отображения А на N Действие, при помощи которого находят сумму, называют сложением, а числа, которые складывают, называют слагаемыми. Используя определение суммы целых неотрицательных чисел, покажем, что 2 + 4 = 6. Возьмем множество А, содержащее 2 элемента и множество В, содержащее 4 элемента, такие, что n(A) = 2, n(B) = 4, A Выясним теоретико-множественный смысл равенства а + 0 = а. Если a=n(A), 0= n( Сложение обладает коммутативностью и ассоциативностью (переместительный и сочетательный законы). Покажем коммутативность. Для любых множеств А и В выполняется равенство А Аналогично можно показать ассоциативность сложения, которая вытекает из равенства (A Действительно, a=n(A), b = n(B),c = n(C) и A В задаче рассматриваются три множества: множество А грибов Кати, множество В – грибов Даши и их объединение. Требуется узнать число элементов в этом объединении, а оно находится сложением. Пусть n(A)=5, n(B)=3, A Дадим теоретико-множественное истолкование суммы нескольких слагаемых, и, используя полученный вывод, найдем сумму 3 + 4 + 2 + 9. Пусть сумма двух слагаемых определена и определена сумма k слагаемых. Тогда сумма, состоящая из k+1 слагаемого, т.е. Значит, чтобы найти сумму 3 + 4 + 2 + 9, согласно этому определению, надо выполнить следующие преобразования: 3 + 4 + 2 + 9 = (3 + 4 + 2) + 9 = ((3 + 4) + 2) + 9 = (7 +2) + 9 = 9 +9 = 18. Найдем значение выражения и объясните, какие законы сложения были при этом использованы: (16 + 9) + 21 + 14. Решение. Используем ассоциативность, что позволяет нам опустить скобки: 16 + 9 + 21 + 14. Используя коммутативность, получим 16 + 14 + 9 + + 21. Используя снова ассоциативность, расставим скобки в нужном нам месте: (16 + 14) + (9 +21). Вычислим значения в скобках: 30 + 30. В итоге получим 60. Значит значение выражения (16 + 9) + 21 + 14 равно 60. Теоретико-множественный смысл разности целых неотрицательных чисел. Определение разности через сумму. Условие существование разности, ее единственность на множестве целых неотрицательных чисел. Правила вычитания числа из суммы и суммы из числа (с доказательством).
Разностью целых неотрицательных чисел а и b называется число элементов в дополнении множества В до множества А при условии, чтоn(A)=a, n(B)=b, B Докажем это. Так как по условию В – собственное подмножество множества А, то их можно представить так, как на рис. 3. Вычитание натуральных (целых неотрицательных) чисел определяется как операция, обратная сложению: а – b = с Разность АВ на этом рисунке заштрихована. Видим, что множества В и АВ не пресекаются и их объединение равно А. Поэтому число элементов в множествеА можно найти по формуле n(A)=n(B) + n(AB), откуда по определению вычитания как операции, обратной сложению, получаем n(AB) = а – b. Аналогичное истолкование получает вычитание нуля, а также вычитание а из а. Так как А Разность а – b целых неотрицательных чисел существует тогда и только тогда, когда Действие, при помощи которого находят разность а – b, называется вычитанием, число а – уменьшаемым, b – вычитаемым. Используя определения, покажем, что 8 – 5 = 3. Пусть даны два множества такие, что n(A) = 8, n(B) = 5. И пусть множество Вявляется подмножеством множества А. Например, А = {a, s, d, f, g, h, j, k}, B = {a, s, d, f, g}. Найдем дополнение множества В до множества А: АВ = {h, j, k}. Получаем, что n(AB) = 3. Следовательно, 8 – 5 = 3. Взаимосвязь вычитания чисел и вычитания множеств позволяет обосновать выбор действия при решении текстовых задач. Выясним, почему следующая задача решается при помощи вычитания, и решите ее: «У школы росло 7 деревьев, из них 3 березы, остальные липы. Сколько лип росло у школы?» Представим условие задачи наглядно, изобразив каждое дерево, посаженное возле школы кружком (рис. 4). Среди них есть 3 березы – на рисунке выделим их штриховкой. Тогда остальные деревья – не заштрихованные кружки – и есть липы. Т. е. их столько, сколько будет из 7 вычесть 3, т. е.4. В задаче рассматриваются три множества: множество А всех деревьев, множество В – берез, которое является подмножеством А, и множество С лип – оно представляет собой дополнение множества В до А. В задаче требуется найти число элементов в этом дополнении. По условию n(A) = 7, n(B) = 3 и B Значит, n(C) = n(AB) = n(A)- n(B) = 7 – 3 = 4. Следовательно, у школы росло 4 липы. Рассматриваемый подход к сложению и вычитанию целых неотрицательных чисел позволяет истолковать с теоретико-множественных позиций различные правила. Правило вычитания числа из суммы: чтобы вычесть число из суммы, достаточно вычесть это число из одного из слагаемых и к полученному результату прибавить другое слагаемое, т.е. при а Выясним смысл данного правила: Пусть А, В, С – такие множества, что n(A)=a, n(B)=b и A Нетрудно доказать с помощью кругов Эйлера, что для данных множеств имеет место равенство Правая часть равенства имеет вид:
Левая часть равенства имеет вид: Правило вычитания суммы из числа: чтобы вычесть из числа сумму чисел, достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим, т.е. при условии, что a Выясним смысл данного правила. Для данных множеств имеет место равенство Тогда получим, что правая часть равенства имеет вид: Следовательно (a + b) – c = (a– c) + b, при условии, что а>c. Правило вычитания разности из числа: чтобы вычесть из числа а разность b – c, достаточно к данному числу прибавить вычитаемое с и из полученного результата вычесть уменьшаемое b; при a > b можно вычесть из числа а уменьшаемое b и к полученному результату прибавить вычитаемое с, т.е. а – (b – c) = (a + c) – b = (a – b) +c. Выясним смысл данного правила: Пусть А, В, С - такие множества, что n(A) = a, n(B) = b, n(C) = c и С Значит, А(ВС) = Следовательно, n(А(ВС)) = n( Правило вычитания числа из разности: чтобы из разности двух чисел вычесть третье число, достаточно из уменьшаемого вычесть сумму двух других чисел, т.е. (а – b) – c = a – (b + c).Доказывается аналогично правилу вычитания суммы из числа. Пример. Какими способами можно найти разность: а) 15 – (5 + 6); б) (12 + 6) – 2? Решение. а) Используем правило вычитания суммы из числа: 15 – (5 + 6) = (15 – 5) – 6 = 10 – 6 = 4. Или 15 – (5 + 6) = (15 – 6) – 5 = 9 – 4 = 4. Или 15 – (5 + 6) = 15 – 11= 4. б) Используем правило вычитания числа из суммы: (12 + 6) – 2 = (12 – 2) + 6 = 10 + 6 = 16. Или (12 + 6) – 2 = 12 + (6 – 2) = 12 + 4 = 16. Или (12 + 6) – 2 = 18 – 2 = 16. Данные правила позволяют упростить вычисления и широко используются в начальном курсе математики.
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 2692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.196 (0.006 с.) |

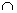 B =
B =  , то суммой целых неотрицательных чисел а и b называется число элементов в объединении множеств А и В, т.е. a + b= n(A) + n(B) = n(A
, то суммой целых неотрицательных чисел а и b называется число элементов в объединении множеств А и В, т.е. a + b= n(A) + n(B) = n(A  B).
B). на множество Х таких чисел, что а + 1
на множество Х таких чисел, что а + 1  х
х  N
N  и Х = {4,5,6,7,8} может быть установлено так: числу с сопоставим х = с + 3, т.е. числу 1 – число 3 + 1 = 4, числу 2 = число 3 + 2 = 5 и т.д.
и Х = {4,5,6,7,8} может быть установлено так: числу с сопоставим х = с + 3, т.е. числу 1 – число 3 + 1 = 4, числу 2 = число 3 + 2 = 5 и т.д. и В на N
и В на N  . Поскольку нет элементов, одновременно принадлежащих А и В, то это отображение определено на всем множестве A
. Поскольку нет элементов, одновременно принадлежащих А и В, то это отображение определено на всем множестве A  равна
равна  .
.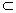 A, т.е. а - b = n(AB). Это обуславливается тем, что А=В
A, т.е. а - b = n(AB). Это обуславливается тем, что А=В  (
(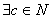 ) b + c = a.
) b + c = a. .
. с имеем, что (a+b)-c=(a-c)+b; при b
с имеем, что (a+b)-c=(a-c)+b; при b  .
. .
. Следовательно(a + b) – c = (a– c) + b,при условии, что а>c.
Следовательно(a + b) – c = (a– c) + b,при условии, что а>c. .
. . Левая часть равенства имеет вид:
. Левая часть равенства имеет вид:  .
. . На рисунке 5 множество А(ВС)изображено штриховкой. Легко убедиться в том, что множество
. На рисунке 5 множество А(ВС)изображено штриховкой. Легко убедиться в том, что множество  изобразится точно такой же областью.
изобразится точно такой же областью. .
. ) и а – (b – c) = (a + c) – b.
) и а – (b – c) = (a + c) – b.


