
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение множеств, свойства пересечения, дистрибутивность пересечения относительно объединения (с доказательством).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пересечение множеств, свойства пересечения, дистрибутивность пересечения относительно объединения (с доказательством). Пересечением множеств А и В называется множество А1В, состоящее только из тех элементов, которые входят и в множество А и в множество В. С=А1В={x| x0A v x0B} 1. Коммутативность: А1В=В1А. 2. Ассоциативность: (А1В)1С=А1(В1С). 3. Дистрибутивность: А1(ВcС)=(А1В)c(А1С). Опр.1.2. Пусть даны множества А и В. Их объединением называется множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В. Объединение множеств обозначается символами "+" и "∪": C=A∪B. Пусть, например, А={-6, -3, 0, 3, 6}, B={0,2, 4, 6, 8}. Тогда A∪B = {-6, -3, 0, 2, 3, 4, 6, 8}.Геометрически объединение множеств изображено. Аналогично определяется объединение большего числа множеств. Объединением множеств А1, А2, А3, …, Аn (обозначение) называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А1, А2, А3, …, Аn. Свойства операции объединения. Теор. 1.1. Справедливы следующие равенства: A∪B = B∪A (коммутативность); (А∪B) ∪C = А (B∪C) (ассоциативность); Если A⊇B, то А∪В= А, объединение А и пустого множества равно А. Док-во. Формулы, подобные формулам 1-2, обычно доказываются так. Берётся элемент, принадлежащий правой части равенства, и доказывается, что он принадлежит левой части. В результате для формулы 1, например, будет доказано, что A∪B ⊆ B∪A. Затем берётся элемент, принадлежащий левой части, и доказывается, что он принадлежит правой части равенства; для формулы 1 это будет означать, что B∪A ⊆ A∪B. Из включений A∪B ⊆ B∪A и B∪A ⊆ A∪B следует, что A∪B = B∪A.
Отношение, как частный случай соответствия. Свойства отношений, особенности графов. Существует много типов бинарных отношений с разными свойствами. Самым общим из этих типов является граф. Это произвольное бинарное отношение, но его особенностью является непривычная терминология - элементы множества, из которого формируются пары, называются вершинами, а сами пары в зависимости от их свойств носят названия ребра или дуги. Графы обычно изображаются не в виде таблицы с двумя колонками (каждая строка такой таблицы представляет пару элементов - вершин), а в виде схемы. Рассмотрим пример. Пусть задано множество вершин V = {a, b, c, d, e}, из которого сформировано некоторое множество пар E = { (a, b), (a, c), (b, d), (c, a), (c, e) }. Множество пар E, сформированное из множества V вершин, является примером бинарного отношения. Преобразуем это бинарное отношение в схему. Для этого изобразим на листе бумаги все его вершины произвольным образом и соединим эти вершины линиями со стрелками так, чтобы каждая стрелка выходила из первого элемента пары и входила во второй элемент пары (см. рисунок 1). При этом, если окажется, что некоторая пара вершин соединяется стрелкой в одну и в другую сторону, то мы вместо линий со стрелками нарисуем линию без стрелок (для нашего примера это пары (a, c) и (c, a)). С учетом этого дугами в графе являются соединительные линии со стрелками в одну сторону, а ребрами - соединения без стрелок или со стрелками, направленными в обе стороны. Можно считать, что каждое ребро содержат пару разнонаправленных дуг.
Рис. 1.
Каждая дуга графа представлена начальной и конечной вершинами. Граф, у которого все связи представлены только ребрами, называется неориентированным графом (или просто графом). Граф, у которого отсутствуют ребра (т.е. все связи имеют только одно направление), называется ориентированным графом, а граф, у которого имеются и ребра, и дуги - смешанным. Если задан граф G, то выражение G (x), где x - произвольная вершина графа, используется для обозначения множества смежных с ней вершин, т.е. вершин, в которые направлена дуга из x. Например, для графа G на рисунке 8 справедливы следующие равенства: G (a) = {b, c}; G (b) = {d}; G (c) = {a, e}; G (d) = G (e) = Æ. Если мы, используя изображение произвольного графа, будем двигаться от вершины к вершине в соответствии с направлением дуг (при этом по ребру можно передвигаться в любую сторону), то последовательность вершин, отмечаемых по мере такого "обхода", называется путем в данном графе. Например для графа G на рисунке 8 существуют следующие пути: (a, b, d); (c, e); (a, c, a, b) и т.д. Пути можно записывать, используя стрелки, например, a®b®d. При этом возможны графы, у которых имеются самопересекающиеся пути, т.е. некоторые вершины и дуги могут в некоторых путях повторяться. Циклом в графе называется такой путь, когда его начальная и конечная вершина совпадают.
Понятие системы счисления. Позиционные и непозиционные системы счисления. Принципы построения позиционных систем. Перевод чисел из системы счисления с одним основанием в систему счисления с другим основанием. Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами. В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы. В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим – десятки. Однако наиболее употребительной оказалась индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр. Различие между позиционой и непозиционной систем счисления легче всего понять на примере сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI. Теоретико-множественный смысл разности целых неотрицательных чисел. Определение разности через сумму. Условие существование разности, ее единственность на множестве целых неотрицательных чисел. Правила вычитания числа из суммы и суммы из числа (с доказательством).
Разностью целых неотрицательных чисел а и b называется число элементов в дополнении множества В до множества А при условии, чтоn(A)=a, n(B)=b, B Докажем это. Так как по условию В – собственное подмножество множества А, то их можно представить так, как на рис. 3. Вычитание натуральных (целых неотрицательных) чисел определяется как операция, обратная сложению: а – b = с Разность АВ на этом рисунке заштрихована. Видим, что множества В и АВ не пресекаются и их объединение равно А. Поэтому число элементов в множествеА можно найти по формуле n(A)=n(B) + n(AB), откуда по определению вычитания как операции, обратной сложению, получаем n(AB) = а – b. Аналогичное истолкование получает вычитание нуля, а также вычитание а из а. Так как А Разность а – b целых неотрицательных чисел существует тогда и только тогда, когда Действие, при помощи которого находят разность а – b, называется вычитанием, число а – уменьшаемым, b – вычитаемым. Используя определения, покажем, что 8 – 5 = 3. Пусть даны два множества такие, что n(A) = 8, n(B) = 5. И пусть множество Вявляется подмножеством множества А. Например, А = {a, s, d, f, g, h, j, k}, B = {a, s, d, f, g}. Найдем дополнение множества В до множества А: АВ = {h, j, k}. Получаем, что n(AB) = 3. Следовательно, 8 – 5 = 3. Взаимосвязь вычитания чисел и вычитания множеств позволяет обосновать выбор действия при решении текстовых задач. Выясним, почему следующая задача решается при помощи вычитания, и решите ее: «У школы росло 7 деревьев, из них 3 березы, остальные липы. Сколько лип росло у школы?» Представим условие задачи наглядно, изобразив каждое дерево, посаженное возле школы кружком (рис. 4). Среди них есть 3 березы – на рисунке выделим их штриховкой. Тогда остальные деревья – не заштрихованные кружки – и есть липы. Т. е. их столько, сколько будет из 7 вычесть 3, т. е.4. В задаче рассматриваются три множества: множество А всех деревьев, множество В – берез, которое является подмножеством А, и множество С лип – оно представляет собой дополнение множества В до А. В задаче требуется найти число элементов в этом дополнении. По условию n(A) = 7, n(B) = 3 и B Значит, n(C) = n(AB) = n(A)- n(B) = 7 – 3 = 4. Следовательно, у школы росло 4 липы. Рассматриваемый подход к сложению и вычитанию целых неотрицательных чисел позволяет истолковать с теоретико-множественных позиций различные правила. Правило вычитания числа из суммы: чтобы вычесть число из суммы, достаточно вычесть это число из одного из слагаемых и к полученному результату прибавить другое слагаемое, т.е. при а Выясним смысл данного правила: Пусть А, В, С – такие множества, что n(A)=a, n(B)=b и A Нетрудно доказать с помощью кругов Эйлера, что для данных множеств имеет место равенство Правая часть равенства имеет вид:
Левая часть равенства имеет вид: Правило вычитания суммы из числа: чтобы вычесть из числа сумму чисел, достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим, т.е. при условии, что a Выясним смысл данного правила. Для данных множеств имеет место равенство Тогда получим, что правая часть равенства имеет вид: Следовательно (a + b) – c = (a– c) + b, при условии, что а>c. Правило вычитания разности из числа: чтобы вычесть из числа а разность b – c, достаточно к данному числу прибавить вычитаемое с и из полученного результата вычесть уменьшаемое b; при a > b можно вычесть из числа а уменьшаемое b и к полученному результату прибавить вычитаемое с, т.е. а – (b – c) = (a + c) – b = (a – b) +c. Выясним смысл данного правила: Пусть А, В, С - такие множества, что n(A) = a, n(B) = b, n(C) = c и С Значит, А(ВС) = Следовательно, n(А(ВС)) = n( Правило вычитания числа из разности: чтобы из разности двух чисел вычесть третье число, достаточно из уменьшаемого вычесть сумму двух других чисел, т.е. (а – b) – c = a – (b + c).Доказывается аналогично правилу вычитания суммы из числа. Пример. Какими способами можно найти разность: а) 15 – (5 + 6); б) (12 + 6) – 2? Решение. а) Используем правило вычитания суммы из числа: 15 – (5 + 6) = (15 – 5) – 6 = 10 – 6 = 4. Или 15 – (5 + 6) = (15 – 6) – 5 = 9 – 4 = 4. Или 15 – (5 + 6) = 15 – 11= 4. б) Используем правило вычитания числа из суммы: (12 + 6) – 2 = (12 – 2) + 6 = 10 + 6 = 16. Или (12 + 6) – 2 = 12 + (6 – 2) = 12 + 4 = 16. Или (12 + 6) – 2 = 18 – 2 = 16. Данные правила позволяют упростить вычисления и широко используются в начальном курсе математики. Понятие площади плоской фигуры и ее измерение. Теорема о площади прямоугольника (с доказательством). Использование понятий равновеликости и равносоставленности при вычислении площадей некоторых плоских фигур. Измерение площади фигуры с помощью палетки. Площадь прямоугольника можно найти следующим образом: S = ab, Где a и b – стороны прямоугольника. Квадрат – это прямоугольник, у которого стороны равны, а, значит, площадь квадрата со стороной a равна a2, то есть S = a2, где а – его сторона. Площадь квадрата можно также вычислить по формуле S = d2/2, где d – диагональ квадрата. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне, то есть вычисляется по формуле S = ah, где а – его сторона, h – высота, проведённая к этой стороне. Площадь параллелограмма можно вычислить и по формуле S = ab sin α, где а и b – стороны, α – угол параллелограмма. Ромб – «частный случай» параллелограмма, значит, его площадь можно находить так же, как и площадь параллелограмма. Кроме того, имеются и другие формулы площади ромба: S = a2 sin α, где а – сторона ромба, α – угол ромба; S = 1/2 d1 d2, где d1и d2 – диагонали ромба. Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне, то есть её можно найти по формуле S = 1/2 ah. Есть и другие формулы для нахождения площади треугольника: S = 1/2 ab sin γ, где а и b – стороны, γ – угол между этими сторонами. При необходимости для нахождения площади треугольника можно использовать формулу Герона,древнегреческого учёного, который жил в Александрии в I веке нашей эры:
где а, b, с – стороны треугольника, p – его полупериметр p = (а + b + с)/2. Площадь трапеции равна произведению полусуммы её оснований на высоту: S = (а + b) / 2 · h, где а и b – основания трапеции, h – высота. Данные формулы позволяют нам решать многие геометрические задачи, рассмотрим некоторые из них. 28. Смысл натурального числа и действий над натуральными числами, полученных в результате измерения величин (на примере длин отрезков). Выясняя смысл натурального числа как меры величины, все рассуждения будем вести на примере одной величины - длины отрезка. Уточним сначала понятие «отрезок состоит из отрезков». Определение. Считают, что отрезок x состоит из отрезков x1, x2, …, xn, если он является их объединением и никакие два из них не имеют общих внутренних точек, хотя и могут иметь общие концы. Пусть задан отрезок х, его длину обозначим Х. выберем из множества отрезков некоторый отрезок е, назовем его единичным отрезком, а длину обозначим буквой Е. Определение: Если отрезок х состоит из отрезков, каждый из которых равен единичному отрезку е, то число а называют численным значением длины Х данного отрезка при единице длины Е. Из данного определения получаем, что натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется. При выбранной единице длины Е это число единственное. В связи с таким подходом к натуральному числу отметим два замечания: – при переходе к другой единице длины численное значение длины заданного отрезка изменяется, хотя сам отрезок остается неизменным. – если отрезок х состоит из а отрезков, равных е, а отрезок у - из b отрезков, тогда а = b тогда и только тогда, когда отрезки х и у равны. Практическая часть Задача 1 Дано множество числовых выражений A={72-5; 19+8; 48:6; 37·2}, на котором задано отношение R: «значение выражения x не больше значения выражения y». Постройте граф отношения R, укажите свойства отношения R. Решение Для того, чтобы построить граф, нужно заметить, что если (x,y) принадлежит «R», то вершины x и y на графе для отношения «R» соединяет соответствующая дуга; если же (x,y) не принадлежит «R», то на графе не будет соединяющей эти вершины дуги.
Задача 2 Используя соответствующие определения, покажите, что:
Сумма (лат. summa – итог, общее количество), результат сложения величин (чисел, функций, векторов, матриц и т. д.). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений: – а + b = b + а 2+4=4+2=6
Разность чисел а и b есть число, которое, будучи прибавлено к b, дает в сумме а. В высшем анализе разностью функции f(x) называют выражение f(x + h) – f(x), в котором букве х можно придавать различные значения, a h сохраняет одно и то же значение. В нашем случае: 5+2 = 7.
Задача 3 Используя соответствующие определения, покажите, что Умножение прямо пропорционально делению, поэтому в нашем случае:
Задача 4 Решите задачу: «Зал и коридор имеют одинаковую длину. Площадь зала равна 300м2, а площадь коридора -120м2. Чему равна ширина коридора, если ширина зала равна 10м, а зал и коридор имеют форму прямоугольника». Решение S1 – площадь зала = 300 кв.м. 1)300: 10= 30 м длина зала S2 – площадь коридора=120 кв. м. 2) 120:30= 4 м ширина коридора Ответ: 4 метра
Задача 5 Вычислить: а) 253т 92кг: 23 – 9т 345кг; б) 4мин 7с · 15 +1мин 15с · 8. Решение а) 253т 92кг: 23 – 9т 345кг
б) 4мин 7с · 15 +1мин 15с · 8
Пересечение множеств, свойства пересечения, дистрибутивность пересечения относительно объединения (с доказательством). Пересечением множеств А и В называется множество А1В, состоящее только из тех элементов, которые входят и в множество А и в множество В. С=А1В={x| x0A v x0B} 1. Коммутативность: А1В=В1А. 2. Ассоциативность: (А1В)1С=А1(В1С). 3. Дистрибутивность: А1(ВcС)=(А1В)c(А1С). Опр.1.2. Пусть даны множества А и В. Их объединением называется множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В. Объединение множеств обозначается символами "+" и "∪": C=A∪B. Пусть, например, А={-6, -3, 0, 3, 6}, B={0,2, 4, 6, 8}. Тогда A∪B = {-6, -3, 0, 2, 3, 4, 6, 8}.Геометрически объединение множеств изображено. Аналогично определяется объединение большего числа множеств. Объединением множеств А1, А2, А3, …, Аn (обозначение) называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А1, А2, А3, …, Аn. Свойства операции объединения. Теор. 1.1. Справедливы следующие равенства: A∪B = B∪A (коммутативность); (А∪B) ∪C = А (B∪C) (ассоциативность); Если A⊇B, то А∪В= А, объединение А и пустого множества равно А. Док-во. Формулы, подобные формулам 1-2, обычно доказываются так. Берётся элемент, принадлежащий правой части равенства, и доказывается, что он принадлежит левой части. В результате для формулы 1, например, будет доказано, что A∪B ⊆ B∪A. Затем берётся элемент, принадлежащий левой части, и доказывается, что он принадлежит правой части равенства; для формулы 1 это будет означать, что B∪A ⊆ A∪B. Из включений A∪B ⊆ B∪A и B∪A ⊆ A∪B следует, что A∪B = B∪A.
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 2132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.110.182 (0.009 с.) |


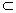 A, т.е. а - b = n(AB). Это обуславливается тем, что А=В
A, т.е. а - b = n(AB). Это обуславливается тем, что А=В  (АВ), т.е. n(A)=n(B) + n(AB).
(АВ), т.е. n(A)=n(B) + n(AB). (
(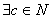 ) b + c = a.
) b + c = a. =А, АА=
=А, АА=  .
. с имеем, что (a+b)-c=(a-c)+b; при b
с имеем, что (a+b)-c=(a-c)+b; при b 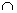 B=
B=  .
. .
. Следовательно(a + b) – c = (a– c) + b,при условии, что а>c.
Следовательно(a + b) – c = (a– c) + b,при условии, что а>c. .
. . Левая часть равенства имеет вид:
. Левая часть равенства имеет вид:  .
. . На рисунке 5 множество А(ВС)изображено штриховкой. Легко убедиться в том, что множество
. На рисунке 5 множество А(ВС)изображено штриховкой. Легко убедиться в том, что множество  изобразится точно такой же областью.
изобразится точно такой же областью. .
. ) и а – (b – c) = (a + c) – b.
) и а – (b – c) = (a + c) – b. ,
,









