
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы – свойства, индексаторыСодержание книги
Поиск на нашем сайте Методы, называемые свойствами (Properties), представляют специальную синтаксическую конструкцию, предназначенную для обеспечения эффективной работы со свойствами. При работе со свойствами объекта (полями) часто нужно решить, какой модификатор доступа использовать, чтобы реализовать нужную стратегию доступа к полю класса. Перечислю пять наиболее употребительных стратегий: · чтение, запись (Read, Write); · чтение, запись при первом обращении (Read, Write-once); · только чтение (Read-only); · только запись (Write-only); · ни чтения, ни записи (Not Read, Not Write). Открытость свойств (атрибут public) позволяет реализовать только первую стратегию. В языке C# принято, как и в других объектных языках, свойства объявлять закрытыми, а нужную стратегию доступа организовывать через методы. Для эффективности этого процесса и введены специальные методы-свойства. Приведу вначале пример, а потом уточню синтаксис этих методов. Рассмотрим класс Person, у которого пять полей: fam, status, salary, age, health, характеризующих соответственно фамилию, статус, зарплату, возраст и здоровье персоны. Для каждого из этих полей может быть разумной своя стратегия доступа. Возраст доступен для чтения и записи, фамилию можно задать только один раз, статус можно только читать, зарплата недоступна для чтения, а здоровье закрыто для доступа и только специальные методы класса могут сообщать некоторую информацию о здоровье персоны. Рассмотрим теперь общий синтаксис методов-свойств. Пусть name - это закрытое свойство. Тогда для него можно определить открытый метод-свойство (функцию), возвращающую тот же тип, что и поле name. Имя метода обычно близко к имени поля (например, Name). Тело свойства содержит два метода - get и set, один из которых может быть опущен. Метод get возвращает значение закрытого поля, метод set - устанавливает значение, используя передаваемое ему значение в момент вызова, хранящееся в служебной переменной со стандартным именем value. Поскольку get и set - это обычные процедуры языка, то программно можно реализовать сколь угодно сложные стратегии доступа. В нашем примере фамилия меняется, только если ее значение равно пустой строке и это означает, что фамилия персоны ни разу еще не задавалась. Статус персоны пересчитывается автоматически при всяком изменении возраста, явно изменять его нельзя. Индексаторы Свойства являются частным случаем метода класса с особым синтаксисом. Еще одним частным случаем является индексатор. Метод-индексатор является обобщением метода-свойства. Он обеспечивает доступ к закрытому полю, представляющему массив. Объекты класса индексируются по этому полю. Синтаксически объявление индексатора - такое же, как и в случае свойств, но методы get и set приобретают аргументы по числу размерности массива, задающего индексы элемента, значение которого читается или обновляется. Важным ограничением является то, что у класса может быть только индексатор со стандартным именем this. Как и любые другие методы индексатор может быть перегруженным. Так что если среди полей класса есть несколько массивов одной размерности, то индексация объектов может быть выполнена только по одному из них. Операции Еще одним частным случаем являются методы, задающие над объектами-классами бинарную или унарную операцию. Введение в класс таких методов позволяет строить выражения, аналогичные арифметическим и булевым выражениям с обычно применяемыми знаками операций и сохранением приоритетов операций. Синтаксис задания таких методов и детали применения опишу чуть позже при проектировании класса рациональных чисел Rational, где введение операций вполне оправдано. Интерфейсы, абстрактные классы, параметрические классы (классы-шаблоны). Исключения. Блок try-catch.
Исключения являются нормальным способом уведомления об ошибках в работе программы. Возникновение ошибки в работе программы должно приводить к выбрасыванию исключения соответствующего типа, следствием чего является прерывание нормального хода выполнения программы и передача управления обработчику исключения - стандартному или предусмотренному самой программой. При программировании в стиле C# ответственность за обнаружение ошибок лежит на вызванной программе. Она должна не только обнаружить ошибку, но и явно сообщить о ней, выбрасывая исключение соответствующего типа. Вызываемая программа должна попытаться исправить последствия ошибки в обработчике исключения.
Try и catch Основу обработки исключительных ситуаций в С# составляет пара ключевых слов try и catch. Эти ключевые слова действуют совместно и не могут быть использованы порознь. Ниже приведена общая форма определения блоков try/catch для обработки исключительных ситуаций: try {// Блок кода, проверяемый на наличие ошибок.}catch (ExcepType1 exOb) {// Обработчик исключения типа ExcepType1.}catch (ExcepType2 exOb) {// Обработчик исключения типа ExcepType2.}...где ExcepType — это тип возникающей исключительной ситуации. Когда исключение генерируется оператором try, оно перехватывается составляющим ему пару оператором catch, который затем обрабатывает это исключение. В зависимости от типа исключения выполняется и соответствующий оператор catch. Так, если типы генерируемого исключения и того, что указывается в операторе catch, совпадают, то выполняется именно этот оператор, а все остальные пропускаются. Когда исключение перехватывается, переменная исключения exOb получает свое значение. На самом деле указывать переменную exOb необязательно. Так, ее необязательно указывать, если обработчику исключений не требуется доступ к объекту исключения, что бывает довольно часто. Для обработки исключения достаточно и его типа. Следует, однако, иметь в виду, что если исключение не генерируется, то блок оператора try завершается как обычно, и все его операторы catch пропускаются. Выполнение программы возобновляется с первого оператора, следующего после завершающего оператора catch. Таким образом, оператор catch выполняется лишь в том случае, если генерируется исключение.
Дискретная математика – Шамшев А.Б.
1. Теория множеств. Основные понятия и определения. Способы задания множеств. Основные операции над множествами Множество - совокупность определенных, вполне различаемых объектов, рассматриваемых как целое. Элемент множества - отдельный объект множества. Пустое множество Æ - множество не содержащее элементов. Универсальное множество (универсум) U – множество, содержащее все возможные элементы в рамках заданного рассмотрения. Мощность множества |M| - количество элементов множества. Если множество конечно и состоит из элементов, сравнимых между собой, то существуют наибольший и наименьший элементы такого множества. Если множество бесконечно и состоит из элементов, сравнимых между собой, то существуют границы этого множества: верхняя и нижняя. Способы задания множеств: Перечисление элементов М = {a1, a2, a3, …, ak} M9 = {1, 2, 3, 4, 5, 6, 7, 8, 9} Выделение определяющего свойства M = { x | P (x)} M9 = { n | n NÎ & n < 10} Определение порождающей процедуры M = { x | x = f} M9 = { n | for n from 1 to 9 write n } Операции над множествами - Объединение AÈB = {x |xÎ A Ú xÎ B} Объединением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В. - Пересечение AÇB = {x |xÎ A & xÎ B} Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В. - Разность A\B = {x |xÎ A & xÏ B} Разностью множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В. - Симметрическая разность A/B = (AÈB)\(AÇB) = {x | (xÎ A & xÏ B) Ú (xÏ A & xÎ B)} Симметрической разностью множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат объединению множеств А и В, и не принадлежат их пересечению. - Дополнение Дополнением множества А до универсального множества называется множество, состоящее из всех тех и только тех элементов, которые принадлежат универсальному множеству, и не принадлежат множеству А. - Прямое произведение множеств Прямым (декартовым) произведением множеств А и В, называется множество А´В, состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству А, вторая - В. А´В = {(a,b) | aÎ A & bÎ B}. А1´А2´...´Аn = {(a1,a2,…,an) | aiÎ Ai, i=1, 2, …, n}. Степенью множества А называется его прямое произведение самого на себя: Аn=A´A´... ´A. Соответственно, А0 = {L}; А1 = A; А2 = A´A; Аn = A´An-1.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.27 (0.008 с.) |

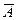 = {x | x Ï A} = U\A, где U - некоторый универсум.
= {x | x Ï A} = U\A, где U - некоторый универсум.


