Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория систем и системный анализ (введение в системный анализ) – евсеева О. Н.Содержание книги
Поиск на нашем сайте
Шкала наименований В основе любого наблюдения и анализа лежат измерения. Измерение - это алгоритмическая операция, которая данному наблюдаемому состоянию объекта ставит в соответствие определенное обозначение: число, номер или символ. Множество обозначений, используемых для регистрации состояний наблюдаемого объекта, называется измерительное шкалой.
Самой слабой качественной шкалой является номинальная (шкала наименований, классификационная шкала), по которой объектам х, или их неразличимым группам дается некоторый признак. Основным свойством этих шкал является сохранение неизменными отношений равенства между элементами эмпирической системы в эквивалентных шкалах. Шкалы номинального типа задаются множеством взаимно однозначных допустимых преобразований шкальных значений. Название «номинальный» объясняется тем, что такой признак дает лишь ничем не связанные имена объектам. Эти значения для разных объектов либо совпадают, либо различаются; никакие более тонкие соотношения между значениями не зафиксированы. Шкалы номинального типа допускают только различение объектов на основе проверки выполнения отношения равенства на множестве этих элементов. Номинальный тип шкал соответствует простейшему виду измерений, при котором шкальные значения используются лишь как имена объектов, поэтому шкалы номинального типа часто называют также шкалами наименований. Примерами измерений в номинальном типе шкал могут служить номера автомашин, телефонов, коды городов, лиц, объектов и т. п. Единственная цель таких измерений выявление различий между объектами разных классов. Если каждый класс состоит из одного объекта, шкала наименований используется для различения объектов.
В общем о шкалах Измерительные шкалы в зависимости от допустимых на них операций различаются по их силе. Самые слабые - номинальные шкалы, а самые сильные - абсолютные. Выделяют три основных атрибута измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории: 1. упорядоченность данных означает, что один пункт шкалы, соответствующий измеряемому свойству, больше, меньше или равен другому пункту; 2. интервальность пунктов шкалы означает, что интервал между любой парой чисел, соответствующих измеряемым свойствам, больше, меньше или равен интервалу между другой парой чисел; 3. нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих измеряемым свойствам, имеет точку отсчета, обозначаемую за ноль, что соответствует полному отсутствию измеряемого свойства. Кроме того, выделяют следующие группы: - неметрические или качественные шкалы, в которых отсутствуют единицы измерений (номинальная и порядковая шкалы); - количественные или метрические (шкала интервалов, шкала отношений и абсолютная шкала).
Шкала порядка В основе любого наблюдения и анализа лежат измерения. Измерение - это алгоритмическая операция, которая данному наблюдаемому состоянию объекта ставит в соответствие определенное обозначение: число, номер или символ. Множество обозначений, используемых для регистрации состояний наблюдаемого объекта, называется измерительное шкалой. Измерительные шкалы в зависимости от допустимых на них операций различаются по их силе. Самые слабые - номинальные шкалы, а самые сильные - абсолютные. Выделяют три основных атрибута измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории: 1. упорядоченность данных означает, что один пункт шкалы, соответствующий измеряемому свойству, больше, меньше или равен другому пункту; 2. интервальность пунктов шкалы означает, что интервал между любой парой чисел, соответствующих измеряемым свойствам, больше, меньше или равен интервалу между другой парой чисел; 3. нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих измеряемым свойствам, имеет точку отсчета, обозначаемую за ноль, что соответствует полному отсутствию измеряемого свойства. Кроме того, выделяют следующие группы: - неметрические или качественные шкалы, в которых отсутствуют единицы измерений (номинальная и порядковая шкалы); - количественные или метрические (шкала интервалов, шкала отношений и абсолютная шкала). Самой слабой качественной шкалой является номинальная (шкала наименований, классификационная шкала), по которой объектам х, или их неразличимым группам дается некоторый признак. Основным свойством этих шкал является сохранение неизменными отношений равенства между элементами эмпирической системы в эквивалентных шкалах. Шкалы номинального типа задаются множеством взаимно однозначных допустимых преобразований шкальных значений. Название «номинальный» объясняется тем, что такой признак дает лишь ничем не связанные имена объектам. Эти значения для разных объектов либо совпадают, либо различаются; никакие более тонкие соотношения между значениями не зафиксированы. Шкалы номинального типа допускают только различение объектов на основе проверки выполнения отношения равенства на множестве этих элементов. Номинальный тип шкал соответствует простейшему виду измерений, при котором шкальные значения используются лишь как имена объектов, поэтому шкалы номинального типа часто называют также шкалами наименований. Примерами измерений в номинальном типе шкал могут служить номера автомашин, телефонов, коды городов, лиц, объектов и т. п. Единственная цель таких измерений выявление различий между объектами разных классов. Если каждый класс состоит из одного объекта, шкала наименований используется для различения объектов.
В общем о шкалах Измерительные шкалы в зависимости от допустимых на них операций различаются по их силе. Самые слабые - номинальные шкалы, а самые сильные - абсолютные. Выделяют три основных атрибута измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории: 1. упорядоченность данных означает, что один пункт шкалы, соответствующий измеряемому свойству, больше, меньше или равен другому пункту; 2. интервальность пунктов шкалы означает, что интервал между любой парой чисел, соответствующих измеряемым свойствам, больше, меньше или равен интервалу между другой парой чисел; 3. нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих измеряемым свойствам, имеет точку отсчета, обозначаемую за ноль, что соответствует полному отсутствию измеряемого свойства. Кроме того, выделяют следующие группы: - неметрические или качественные шкалы, в которых отсутствуют единицы измерений (номинальная и порядковая шкалы); количественные или метрические (шкала интервалов, шкала отношений и абсолютная шкала). Шкала отношений В основе любого наблюдения и анализа лежат измерения. Измерение - это алгоритмическая операция, которая данному наблюдаемому состоянию объекта ставит в соответствие определенное обозначение: число, номер или символ. Множество обозначений, используемых для регистрации состояний наблюдаемого объекта, называется измерительное шкалой. Измерительные шкалы в зависимости от допустимых на них операций различаются по их силе. Самые слабые - номинальные шкалы, а самые сильные - абсолютные. Выделяют три основных атрибута измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории: 1. упорядоченность данных означает, что один пункт шкалы, соответствующий измеряемому свойству, больше, меньше или равен другому пункту; 2. интервальность пунктов шкалы означает, что интервал между любой парой чисел, соответствующих измеряемым свойствам, больше, меньше или равен интервалу между другой парой чисел; 3. нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих измеряемым свойствам, имеет точку отсчета, обозначаемую за ноль, что соответствует полному отсутствию измеряемого свойства. Кроме того, выделяют следующие группы: - неметрические или качественные шкалы, в которых отсутствуют единицы измерений (номинальная и порядковая шкалы); - количественные или метрические (шкала интервалов, шкала отношений и абсолютная шкала)..
Формально шкалой называется кортеж из трех элементов Шкалой отношений {подобия) называется шкала, если Нетрудно убедиться, что в шкалах отношений остаются неизменными отношения численных оценок объектов. Действительно, пусть в одной шкале объектам
Данное соотношение объясняет название шкал отношений. Шкалы отношений, являясь частным случаем шкал интервалов, при выборе нулевой точки отсчета сохраняют не только отношения свойств объектов, но и отношения расстояний между парами объектов. Этот тип шкалы удобен для измерения весов, длин и т. д. Сильные и слабые шкалы В основе любого наблюдения и анализа лежат измерения. Измерение - это алгоритмическая операция, которая данному наблюдаемому состоянию объекта ставит в соответствие определенное обозначение: число, номер или символ. Множество обозначений, используемых для регистрации состояний наблюдаемого объекта, называется измерительное шкалой. Измерительные шкалы в зависимости от допустимых на них операций делятся на «слабые» (номинальная, порядковая) и «сильные» (шкала интервалов, периодическая шкала, шкала отношений, абсолютная шкала). Сила шкалы оценивается по возможностям дальнейшей обработки результатов. 1. Абсолютная шкала. Допустимое преобразование для шкал данного типа представляет собой тождество, т. е. если на одном языке в протоколе записано 2. Шкала отношений. Между разными протоколами, фиксирующими один и тот же эмпирический факт на разных языках, при этом типе шкалы должно выполняться соотношение: 3. Шкала интервалов. Здесь между протоколами
Если записи в протоколе сопровождаются информацией о том, какие именно градусы имеются в виду (например, 18 °С), то мы имеем дело с протоколом в абсолютной шкале. 4. Шкала порядка. Допустимыми преобразованиями для данного типа шкалы являются все монотонные преобразования, т. е. такие, которые не нарушают порядок следования значений измеряемых величин. Такие протоколы появляются, например, в результате сравнения тел по твердости. Записи «1; 2; 3» и «5,3; 12,5; 109,2» содержат одинаковую информацию о том, что первое тело самое твердое, второе менее твердое, а третье — самое мягкое. И никакой информации о том, во сколько раз одно тверже другого, на сколько единиц оно тверже, в этих записях нет и полагаться на конкретные значения чисел, на их отношения или разности нельзя. Разновидностью шкалы порядка является шкала рангов, где используются только числа, идущие подряд от 1 вверх по возрастанию. К типу шкал порядка относится и широко используемая шкала баллов. При этом используются целые числа в ограниченном диапазоне их значений: от 1 до 5 в системе образования, от 0 до 6 или 10 в спорте и т. д. В любом из этих случаев протокол содержит информацию только о трех эмпирических отношениях: <, > и =. 5. Шкала наименований. Здесь фиксируется только два отношения: «равно» и «не равно». Следовательно, допустимы любые преобразования, лишь бы в протоколе одинаковые объекты были поименованы одинаковыми символами (числами, буквами, словами), а разные объекты имели разные имена. Так фиксируются в протоколах такие характеристики, как собственные имена людей, их национальность, названия населенных пунктов и т. п. Критерии принятия решений Критерий принятия решений - это функция, выражающая предпочтения лица принимающего решения и определяющая правило, по которому выбирается приемлемый или оптимальный вариант решения. Задача принятия решений возникает тогда, когда возникает несколько конкурирующих вариантов решения. В противном случае ситуация предопределена. В классическом случае описание ситуации дается в виде матрицы, строки которой соответствуют вариантам решений, а столбцы - факторам, которые могут повлиять на результат, получаемый ЛПР. Минимаксный критерий. Правило выбора решения в соответствии с минимаксным критерием (ММ-критерием) можно интерпретировать следующим образом: матрица решений дополняется еще одним столбцом из наименьших результатов eir каждой строки. Необходимо выбрать те варианты в строках которых стоят наибольшее значение eir этого столбца. Выбранные т.о. варианты полностью исключают риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство позволяет считать ММ-критерий одним из фундаментальных. Применение ММ-критерия бывает оправдано, если ситуация, в которой принимается решение следующая: 1. О возможности появления внешних состояний Fj ничего не известно; 2. Приходится считаться с появлением различных внешних состояний Fj; 3. Решение реализуется только один раз; 4. Необходимо исключить какой бы то ни было риск. Критерий Байеса—Лапласа. Обозначим через qi — вероятность появления внешнего состояния Fj. Соответствующее правило выбора можно интерпретировать следующим образом: матрица решений дополняется еще одним столбцом содержащим математическое ожидание значений каждой из строк. Выбираются те варианты, в строках которых стоит наибольшее значение eir этого столбца. При этом предполагается, что ситуация, в которой принимается решение, характеризуется следующими обстоятельствами: 1. Вероятности появления состояния Fj известны и не зависят от времени. 2. Решение реализуется (теоретически) бесконечно много раз. 3. Для малого числа реализаций решения допускается некоторый риск. При достаточно большом количестве реализаций среднее значение постепенно стабилизируется. Поэтому при полной (бесконечной) реализации какой-либо риск практически исключен. Т.о. критерий Байеса-Лапласа (B-L-критерий) более оптимистичен, чем минимаксный критерий, однако он предполагает большую информированность и достаточно длительную реализацию. Критерий Сэвиджа. aij:= maxi(eij) - eij eir:= maxi(aij) = maxj(maxi(eij) - eij) Величину aij можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Fj вместо варианта Ei выбирать другой, оптимальный для этого внешнего состояния вариант. Величину aij можно интерпретировать и как потери (штрафы) возникающие в состоянии Fj при замене оптимального для него варианта на вариант Ei. В последнем случае eir представляет собой максимально возможные (по всем внешним состояниям Fj, j = {1,n}) потери в случае выбора варианта Ei. Соответствующее критерию Сэвиджа правило выбора теперь трактуется так: 1. Каждый элемент матрицы решений ||eij|| вычитается из наибольшего результата max(eij) соответствующего столбца. 2. Разности aij образуют матрицу остатков ||eij||. Эта матрица пополняется столбцом наибольших разностей eir. Выбирают те варианты, в строках которых стоит наименьшее для этого столбца значение. Требования, предъявляемые к ситуации, в которой принимается решение, совпадают с требованием к ММ-критерию. Производные критерии. Критерий Гурвица. Стараясь занять наиболее уравновешенную позицию, Гурвиц предположил оценочную функцию, которая находится где-то между точкой зрения крайнего оптимизма и крайнего пессимизма: maxi(eir) = { C⋅minj(eij) + (1-C)⋅maxj(eij) }, где С — весовой множитель. Правило выбора согласно критерию Гурвица, формируется следующим образом: матрица решений ||eij|| дополняется столбцом, содержащим среднее взвешенное наименьшего и наибольшего результатов для каждой строки. Выбираются только те варианты, в строках которых стоят наибольшие элементы eir этого столбца. При С=1 критерий Гурвица превращается в ММ-критерий. При С = 0 он превращается в критерий «азартного игрока» maxi(eir) = maxi(maxj(eij)), т.е. мы становимся на точку зрения азартного игрока, делающего ставку на то, что «выпадет» наивыгоднейший случай. В технических приложениях сложно выбрать весовой множитель С, т.к. трудно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Поэтому чаще всего С:=1/2. Критерий Гурвица применяется в случае, когда: 1. о вероятностях появления состояния Fj ничего не известно; 2. с появлением состояния Fj необходимо считаться; 3. реализуется только малое количество решений; 4. допускается некоторый риск. Критерий Ходжа–Лемана. Этот критерий опирается одновременно на ММ-критерий и критерий Баеса-Лапласа. С помощью параметра v выражается степень доверия к используемому распределений вероятностей. Если доверие велико, то доминирует критерий Баеса-Лапласа, в противном случае — ММ-критерий, т.е. мы ищем maxi(eir) = maxi{ v ⋅∑eij⋅qi + (1- v) minj(eir)}, 0 ≤ v ≤ 1. Правило выбора, соответствующее критерию Ходжа-Лемана формируется следующим образом: матрица решений ||eij|| дополняется столбцом, составленным из средних взвешенных (с весом v ≡const) математическое ожиданиями и наименьшего результата каждой строки. Отбираются те варианты решений в строках которого стоит набольшее значение этого столбца. При v = 1 критерий Ходжа-Лемана переходит в критерий Байеса-Лапласа, а при v = 0 становится минимаксным. Выбор v субъективен т. к. степень достоверности какой-либо функции распределения - дело темное. Для применения критерия Ходжа-Лемана желательно, чтобы ситуация в которой принимается решение, удовлетворяла свойствам: 1. вероятности появления состояния Fj неизвестны, но некоторые предположения о распределении вероятностей возможны; 2. принятое решение теоретически допускает бесконечно много реализаций; 3. при малых числах реализации допускается некоторый риск. Критерий Гермейера. Этот критерий ориентирован на величину потерь, т.е. на отрицательные значения всех eij. При этом maxi(eir) = maxi(minj(eij)qj). Т.к. в хозяйственных задачах преимущественно имеют дело с ценами и затратами, условие eij<0 обычно выполняется. В случае же, когда среди величин eij встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования eij-a при подходящем образом подобранном a>0. При этом оптимальный вариант решения зависит от а. Правило выбора согласно критерию Гермейера формулируется следующим образом: матрица решений ||eij|| дополняется еще одним столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния Fj. Выбираются те варианты в строках которых находится наибольшее значениеe eij этого столбца. Условия его применимости таковы: 1. вероятности появления состояния Fj неизвестны; 2. с появлением тех или иных состояний, отдельно или в комплексе, необходимо считаться; 3. допускается некоторый риск; 4. решение может реализоваться один или несколько раз. Если функция распределения известна не очень надежно, а числа реализации малы, то, следуя критерию Гермейера, получают, вообще говоря, неоправданно большой риск. Метод анализа иерархий Метод анализа иерархий (МАИ) является систематической процедурой для иерархического представления элементов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на более простые составляющие части (от цели до сравниваемых вариантов решения проблем или альтернатив) и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена относительная степень (интенсивность) взаимодействия элементов в иерархии. Эти суждения затем выражаются численно. Метод анализа иерархии включает процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений. Действие метода анализа иерархий основывается на следующих принципах: Ø Принцип идентичности и декомпозиции; Ø Принцип дискриминации и сравнительных суждений; Ø Принцип синтезирования. Принцип идентичности и декомпозиции предусматривает структурирование проблем в виде иерархии или сети, что является первым этапом применения МАИ. 1 шаг. Декомпозиция. Обозначается общая цель, факторы (критерии), уточняющие цель, кандидаты, которые должны быть оценены по отношению к критериям. 2 шаг. Установление приоритетов критериев и оценка альтернатив. Обозначаются веса для каждого критерия. Составляются матрицы парных сравнений для каждого критерия. Матрицу сравнения можно получить нахождением отношений заранее известных весов элементов. Если веса неизвестны, то используется шкала относительной важности, в которой в зависимости от того какой из двух объектов важнее показателю сравнительной важности присваиваются - число 1, если объекты одинаково важны; - числа от 2 до 9, если первый объект важнее второго; - числа от 1/9 до ½, если второй объект важнее первого. 3 шаг. Синтез приоритетов. По матрицам парных сравнений формируют набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня. Для этого нужно вычислить множество собственных векторов для каждой матрицы, и затем нормализовать результат, получив тем самым вектор приоритетов. Оценки, получаемые в процессе заполнения матриц парных сравнений, оценки локальных приоритетов должны быть согласованными, что определяется с помощью индекса согласованности (ИС).ИС сравнивают с той величиной, которая получилась бы при случайном выборе количественных суждений из шкалы 1/9, 1/8, …, 1, 2, …, 9 в обратносимметричной матрице. При делении ИС на число, соответствующее случайной согласованности матрицы того же порядка, получают отношение согласованности (ОС), величина которого не должна превышать 10%, чтобы быть приемлемой. В некоторых случаях допускается значение ОС до 20%. Если ОС выходит из указанных пределов, то необходимо заново исследовать задачу и проверить полученные оценки (суждения). В итоге вычисляется глобальный приоритет того элемента, который затем используется для взвешивания локальных приоритетов элементов, сравниваемых по отношению к нему как к критерию и расположенных уровнем ниже.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.103 с.) |

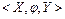 , где
, где  реальный объект,
реальный объект,  шкала,
шкала,  гомоморфное отображение
гомоморфное отображение  состоит из преобразований подобия
состоит из преобразований подобия  ,
, 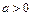 , где
, где 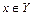 - шкальные значения из области определения
- шкальные значения из области определения  – действительные числа.
– действительные числа.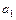 и
и  соответствуют шкальные Значения
соответствуют шкальные Значения 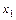 и
и  , а в другой
, а в другой  и
и  , где
, где  .
. , а на другом языке
, а на другом языке  , то между ними должно выполняться простое соотношение:
, то между ними должно выполняться простое соотношение:  . Этот тип шкалы удобен для записи количества элементов в некотором конечном множестве. Если, пересчитав количество яблок, один запишет в протоколе 6, а другой запишет VI, то нам достаточно знать, что 6 и VI означают одно и то же, т. е. что между этими записями существует тождественное отношение: 6 = VI.
. Этот тип шкалы удобен для записи количества элементов в некотором конечном множестве. Если, пересчитав количество яблок, один запишет в протоколе 6, а другой запишет VI, то нам достаточно знать, что 6 и VI означают одно и то же, т. е. что между этими записями существует тождественное отношение: 6 = VI.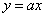 , где
, где  — любое положительное число. Один и тот же эмпирический смысл имеют протоколы: 16 кг, 16000 г, 0,016 т, 1 пуд, 40 фунтов. От любой записи можно перейти к любой другой, подобрав соответствующий множитель
— любое положительное число. Один и тот же эмпирический смысл имеют протоколы: 16 кг, 16000 г, 0,016 т, 1 пуд, 40 фунтов. От любой записи можно перейти к любой другой, подобрав соответствующий множитель  , где
, где  может быть как положительным, так и отрицательным. Это значит, что в разных протоколах может использоваться разный масштаб единиц
может быть как положительным, так и отрицательным. Это значит, что в разных протоколах может использоваться разный масштаб единиц  и разные начала отсчета
и разные начала отсчета 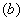 . Примером шкал этого типа могут быть шкалы для измерения температуры. Если в протоколе указаны градусы, но не говорится в какой шкале (Цельсия, Кельвина и т. д.), то во избежание недоразумений при описании закономерностей можно использовать только отношения интервалов, так как при любых значениях
. Примером шкал этого типа могут быть шкалы для измерения температуры. Если в протоколе указаны градусы, но не говорится в какой шкале (Цельсия, Кельвина и т. д.), то во избежание недоразумений при описании закономерностей можно использовать только отношения интервалов, так как при любых значениях